Guia completo: como interpretar resultados de anova no excel

Uma ANOVA unidirecional é usada para determinar se há ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes.

O exemplo a seguir fornece um guia completo sobre como interpretar os resultados de uma ANOVA unidirecional no Excel.

Exemplo: como interpretar resultados de ANOVA no Excel

Suponha que um professor peça aleatoriamente a 30 alunos de sua turma que usem um dos três métodos de estudo para se prepararem para um exame.

A captura de tela a seguir mostra as pontuações dos alunos com base no método usado:

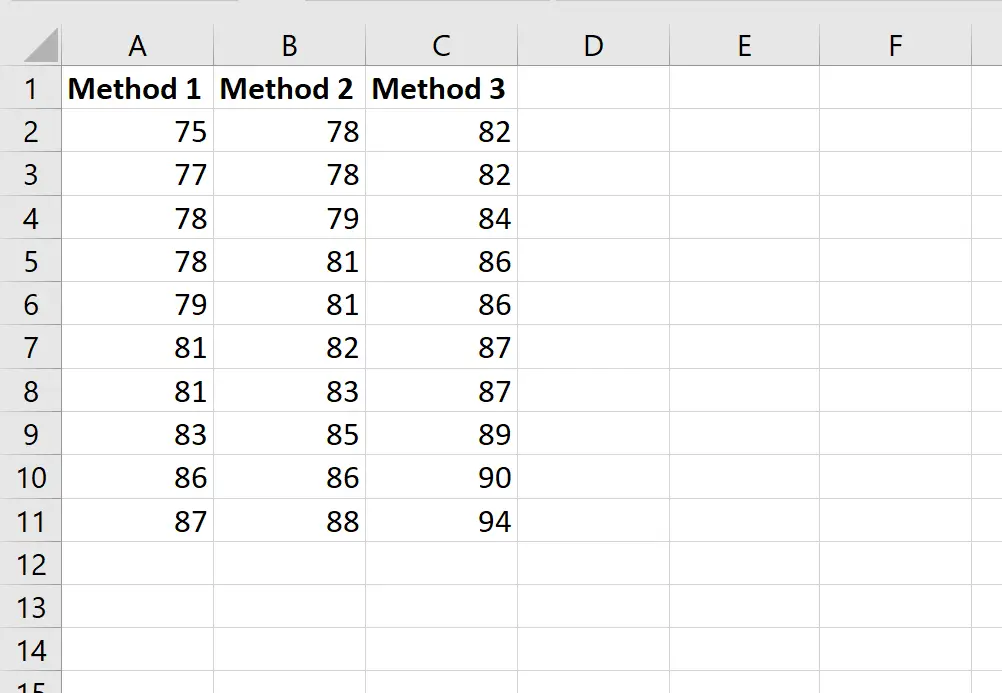
Suponha que o professor queira realizar uma ANOVA unidirecional para determinar se as pontuações médias são iguais nos três grupos.

Para realizar uma ANOVA unidirecional no Excel, clique na guia Dados na faixa superior e clique em Análise de Dados no grupo Analisar .

Se você não vir a opção Análise de dados , primeiro deverá carregar o software gratuito Analysis ToolPak .

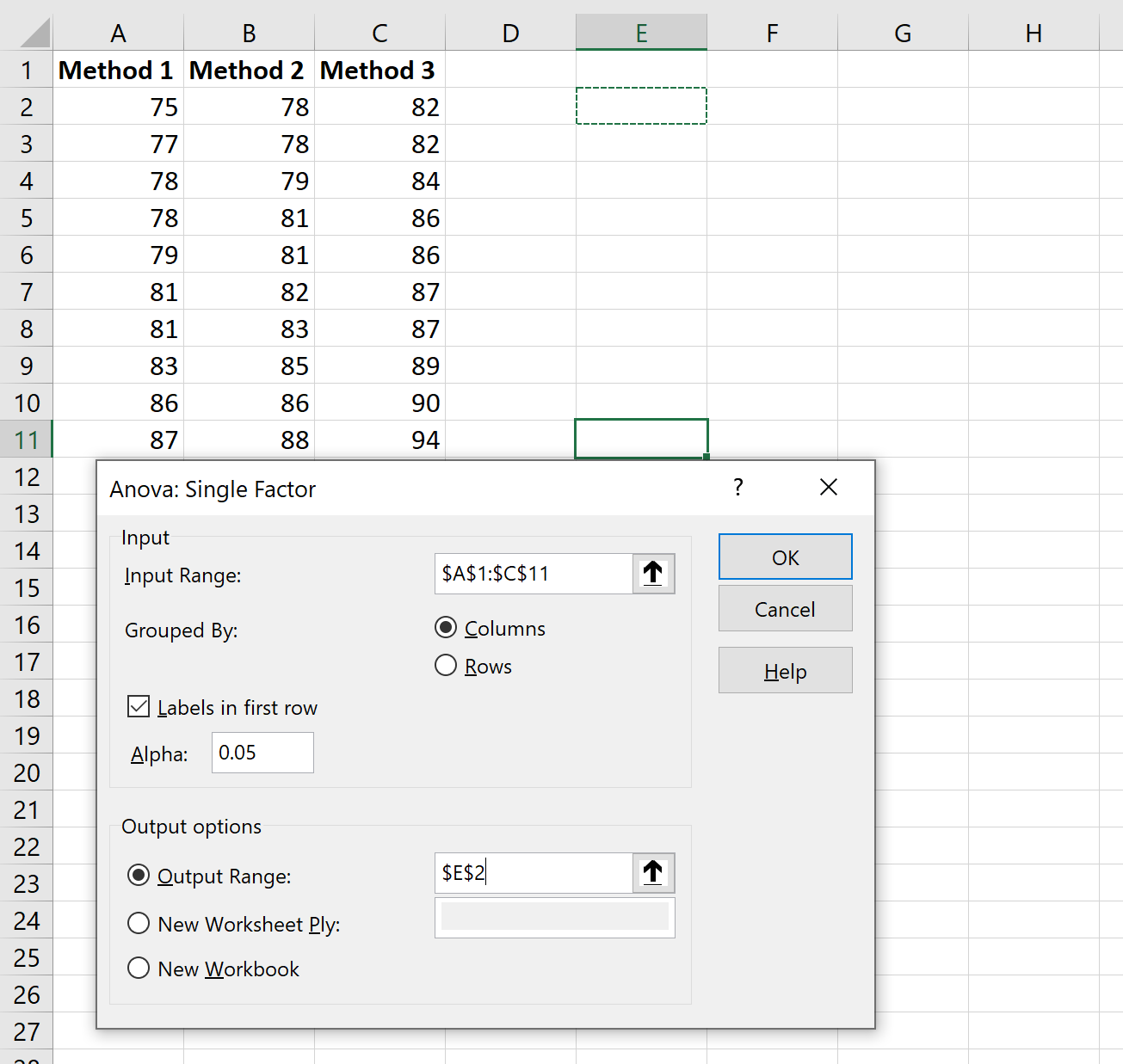
Depois de clicar nele, uma nova janela aparecerá. Selecione Anova: fator único e clique em OK .

Na nova janela que aparece, insira as seguintes informações:

Depois de clicar em OK , os resultados da ANOVA unidirecional aparecerão:

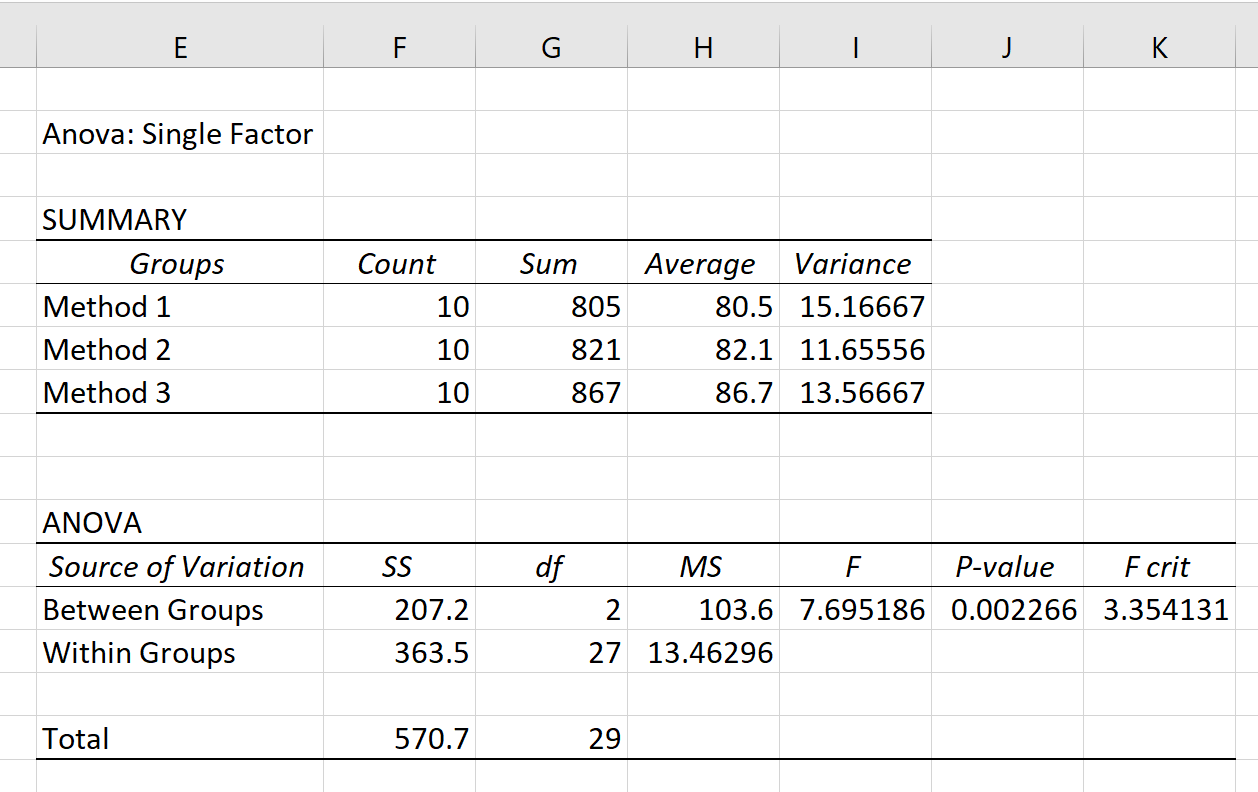
Duas tabelas são exibidas no resultado: SUMMARY e ANOVA .

Veja como interpretar os valores de cada tabela:

Tabela RESUMO :

• Grupos : nomes de grupos
• Contagem : O número de observações em cada grupo
• Soma : A soma dos valores de cada grupo
• Média : O valor médio em cada grupo
• Variância : A variação dos valores em cada grupo

Esta tabela nos fornece vários resumos estatísticos úteis para cada grupo usado na ANOVA.

Nesta tabela podemos verificar que os alunos que utilizaram o Método 3 tiveram a nota média mais elevada nos exames (86,7), mas também tiveram a maior variação nas notas dos testes. revisão (13.56667).

Para determinar se as diferenças nas médias dos grupos são estatisticamente significativas, devemos consultar a tabela ANOVA.

Tabela ANOVA :

• Fonte de variação : a variação medida (entre grupos ou dentro de grupos)
• SS : A soma dos quadrados para cada fonte de variação
• df : Os graus de liberdade, calculados como #groups-1 para df Between e #observations – #groups para df Within
• MS : A soma média dos quadrados, calculada em SS/df
• F : O valor F geral, calculado como MS Entre / MS Dentro
• Valor P : O valor p correspondente ao valor F geral
• F crit : O valor crítico F que corresponde a α = 0,05

O valor mais importante nesta tabela é o valor p , que acaba sendo 0,002266 .

Lembre-se de que uma ANOVA unidirecional usa as seguintes hipóteses nulas e alternativas:

• H ₀ : Todas as médias do grupo são iguais.
• _HA : Nem todas as médias dos grupos são iguais.

Como o valor p é menor que α = 0,05, rejeitamos a hipótese nula da ANOVA unidirecional e concluímos que temos evidências suficientes para afirmar que todas as médias dos grupos não são iguais.

Isso significa que nem todos os três métodos de estudo levam às mesmas notas médias nos exames.

Nota : Você também pode comparar o valor F geral com o valor F crítico para determinar se deve ou não rejeitar a hipótese nula. Neste caso, como o valor global de F é maior que o valor crítico de F, rejeitaríamos a hipótese nula. Observe que a abordagem do valor p e a abordagem do valor F crítico sempre levarão à mesma conclusão.

Recursos adicionais

Os tutoriais a seguir explicam como realizar diferentes ANOVAs no Excel:

Como realizar ANOVA unidirecional no Excel
Como realizar uma ANOVA bidirecional no Excel
Como realizar ANOVA de medidas repetidas no Excel
Como realizar ANOVA aninhada no Excel