Intervalo de confiança para diferença de proporções
Um intervalo de confiança (IC) para uma diferença em proporções é um intervalo de valores que provavelmente contém a verdadeira diferença entre duas proporções populacionais com um certo nível de confiança.
Este tutorial explica o seguinte:
- A motivação para criar esse intervalo de confiança.
- A fórmula para criar esse intervalo de confiança.
- Um exemplo de como calcular esse intervalo de confiança.
- Como interpretar este intervalo de confiança.
IC para diferença de proporções: motivação
Os pesquisadores muitas vezes desejam estimar a diferença entre duas proporções populacionais. Para estimar essa diferença, eles coletarão uma amostra aleatória de cada população e calcularão a proporção para cada amostra. Então eles podem comparar a diferença entre as duas proporções.
No entanto, não podem saber com certeza se a diferença entre as proporções da amostra corresponde à verdadeira diferença entre as proporções da população. É por isso que podem criar um intervalo de confiança para a diferença entre as duas proporções. Isso fornece uma gama de valores que provavelmente conterá a verdadeira diferença entre as proporções populacionais.
Por exemplo, suponha que queiramos estimar a diferença entre a proporção de residentes que apoiam uma determinada lei no Condado A e a proporção que apoiam a lei no Condado B.
Como existem milhares de residentes em cada condado, seria muito demorado e caro pesquisar cada residente individual em cada condado.
Em vez disso, poderíamos pegar uma amostra aleatória simples de residentes de cada condado e usar a proporção a favor da lei em cada amostra para estimar a verdadeira diferença nas proporções entre os dois condados:
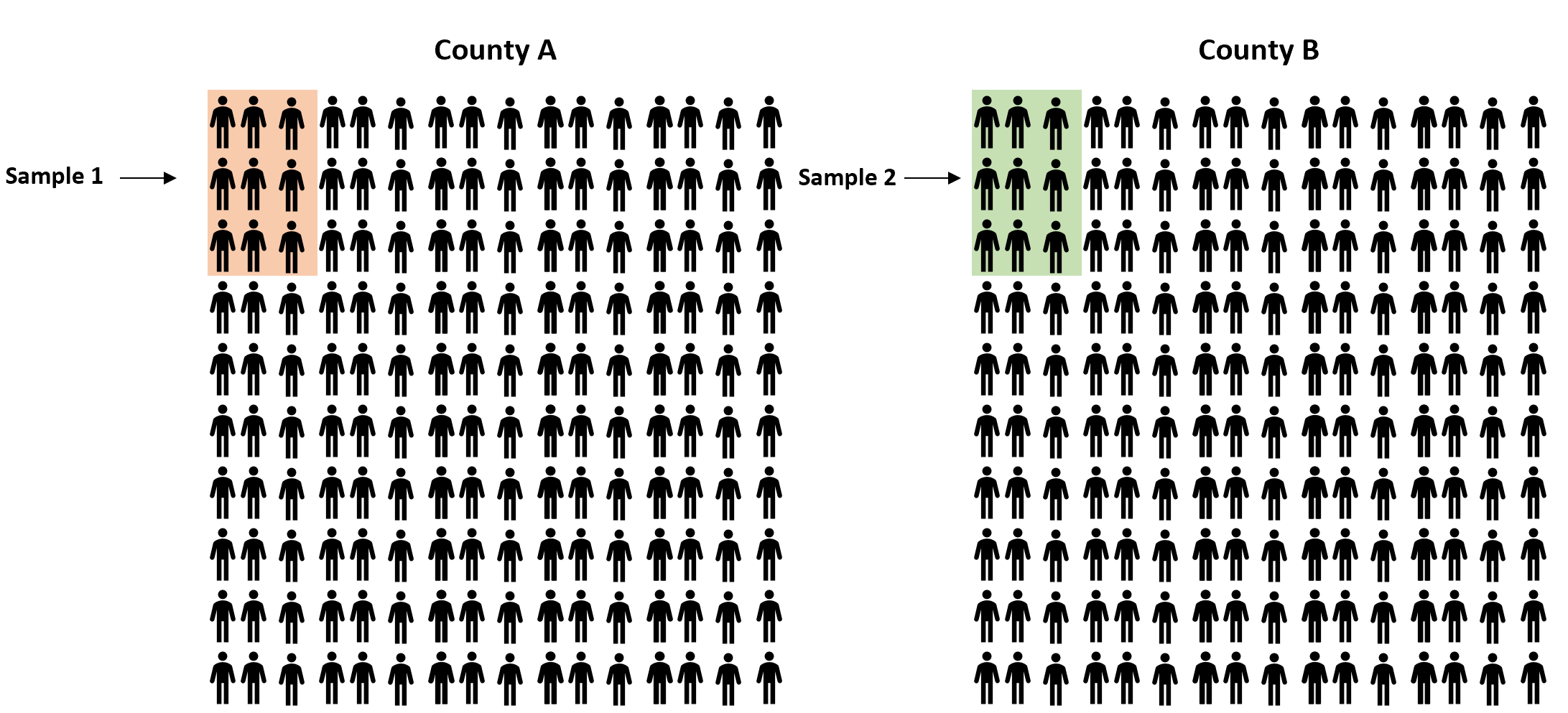
Como as nossas amostras são aleatórias, não é garantido que a diferença de proporções entre as duas amostras corresponda exatamente à diferença de proporções entre as duas populações. Assim, para capturar esta incerteza, podemos criar um intervalo de confiança contendo uma faixa de valores que provavelmente conterá a verdadeira diferença de proporções entre as duas populações.
CI para a diferença de proporções: fórmula
Usamos a seguinte fórmula para calcular um intervalo de confiança para a diferença entre duas proporções populacionais:
Intervalo de confiança = (p 1 –p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )
Ouro:
- p 1 , p 2 : proporção da amostra 1, proporção da amostra 2
- z: o valor crítico z com base no nível de confiança
- n 1 , n 2 : tamanho da amostra 1, tamanho da amostra 2
O valor z usado depende do nível de confiança escolhido. A tabela a seguir mostra o valor z que corresponde às opções de nível de confiança mais comuns:
| Um nível de confiança | valor z |
|---|---|
| 0,90 | 1.645 |
| 0,95 | 1,96 |
| 0,99 | 2,58 |
Observe que níveis de confiança mais elevados correspondem a valores z maiores, o que leva a intervalos de confiança mais amplos. Isto significa que, por exemplo, um intervalo de confiança de 95% será maior do que um intervalo de confiança de 90% para o mesmo conjunto de dados.
CI para a diferença de proporções: exemplo
Suponha que queiramos estimar a diferença entre a proporção de residentes que apoiam uma determinada lei no condado A em comparação com a proporção que apoia a lei no condado B. Aqui estão os dados resumidos para cada amostra:
Amostra 1:
- n 1 = 100
- p 1 = 0,62 (ou seja, 62 habitantes em cada 100 apoiam a lei)
Amostra 2:
- n2 = 100
- p 2 = 0,46 (ou seja, 46 habitantes em cada 100 apoiam a lei)
Veja como encontrar diferentes intervalos de confiança para a diferença nas proporções populacionais:
Intervalo de confiança de 90%:
(0,62-0,46) +/- 1,645*√(0,62(1-0,62)/100 + 0,46(1-0,46)/100) = [0,0456, 0,2744]
Intervalo de confiança de 95%:
(0,62-0,46) +/- 1,96*√(0,62(1-0,62)/100 + 0,46(1-0,46)/100) = [0,0236, 0,2964]
Intervalo de confiança de 99%:
(0,62-0,46) +/- 2,58*√(0,62(1-0,62)/100 + 0,46(1-0,46)/100) = [-0,0192, 0,3392]
Nota: Você também pode encontrar esses intervalos de confiança usando a Calculadora de Intervalo de Confiança para Diferença de Proporções .
IC para a diferença de proporções : interpretação
A maneira como interpretaríamos um intervalo de confiança é:
Há uma probabilidade de 95% de que o intervalo de confiança de [0,0236, 0,2964] contenha a verdadeira diferença na proporção de residentes que apoiam a lei entre os dois condados.
Dado que este intervalo não contém o valor “0”, isto significa que é muito provável que exista uma verdadeira diferença na proporção de residentes que apoiam esta lei no Condado A em comparação com o Condado B.