Intervalo de confiança para a diferença de médias
Este artigo explica o que é um intervalo de confiança para a diferença de médias nas estatísticas e para que ele é usado. Assim, você descobrirá como calcular o intervalo de confiança para a diferença de duas médias e um exercício resolvido passo a passo.
Qual é o intervalo de confiança para a diferença de médias?
O intervalo de confiança para a diferença de médias é um intervalo que fornece um valor máximo e um valor mínimo entre os quais o valor da diferença de médias de duas populações se encontra com um certo nível de confiança.
Por exemplo, se o intervalo de confiança para a diferença nas médias de duas populações com um nível de confiança de 95% for (3,5), isso significa que a diferença entre as médias das duas populações estará entre 3 e 5 com uma probabilidade de 95 %.
Portanto, nas estatísticas, o intervalo de confiança para a diferença de médias é usado para estimar dois valores entre os quais se encontra a diferença entre duas médias populacionais. Assim, utilizando dados de duas amostras, é possível aproximar a diferença entre as médias populacionais.
Fórmula de intervalo de confiança para diferença de médias
A fórmula para o intervalo de confiança para a diferença nas médias depende de as variâncias populacionais serem ou não conhecidas e, caso contrário, se as variâncias populacionais podem ou não ser consideradas iguais. . Veremos então como o intervalo de confiança para a diferença de médias é calculado em cada caso.
desvios conhecidos
A fórmula para calcular o intervalo de confiança para a diferença de médias quando as variâncias das duas populações são conhecidas com um nível de confiança de 1-α é a seguinte:
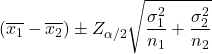
Ouro:
-

é a média da amostra i.
-

é o desvio padrão da população i.
-

é o valor da distribuição normal padrão com probabilidade α/2.
-

é o tamanho da amostra i.
Este caso é o menos comum, uma vez que o valor das variâncias populacionais é geralmente desconhecido.
variâncias desconhecidas e iguais
Quando as variâncias das duas populações são desconhecidas, mas podem ser estimadas como iguais, a fórmula para calcular o intervalo de confiança para a diferença de médias com um nível de confiança de 1-α é a seguinte:
![]()
Ouro:
-

é a média da amostra i.
-

é o desvio padrão combinado.
-

é o valor da distribuição t de Student de n 1 + n 2 -2 graus de liberdade com probabilidade de α/2.
-

é o tamanho da amostra i.
Como neste caso se assume que as variâncias populacionais são equivalentes, o desvio padrão combinado é utilizado para calcular o intervalo de confiança, que é calculado com a seguinte fórmula:

Ouro
![]()
é o desvio padrão da amostra i.
Variações desconhecidas e diferentes
Quando as variâncias das duas populações são desconhecidas e não podem ser consideradas iguais, a fórmula para calcular o intervalo de confiança para a diferença de médias com um nível de confiança de 1-α é a seguinte:
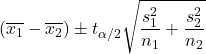
Ouro:
-

é a média da amostra i.
-
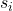
é o desvio padrão da amostra i.
-

é o valor da distribuição t de Student com probabilidade de α/2.
-

é o tamanho da amostra i.
Neste caso, os graus de liberdade da distribuição t de Student são calculados através da seguinte fórmula:

Ouro
![]()
é o desvio padrão da amostra i.
Exemplo concreto do intervalo de confiança para a diferença de médias
Depois de ver a definição do intervalo de confiança para a diferença de médias e quais são as diferentes fórmulas, veremos agora um exemplo concreto para terminar de assimilar como é calculado o intervalo de confiança para a diferença de duas médias.
- Queremos estudar o efeito do tabaco no peso ao nascer das crianças. Para isso, são comparadas duas amostras: a primeira amostra é composta por crianças cujas mães não fumavam e a segunda amostra é composta por crianças cujas mães fumavam (os parâmetros da amostra estão indicados abaixo). Calcule o intervalo de confiança para a diferença de médias com um nível de confiança de 95%.
- Mães não fumantes:
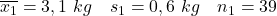
- Mães fumantes:
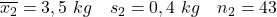
- Mães não fumantes:
Neste caso não conhecemos os valores das variâncias populacionais, porém, podemos assumir que as variâncias populacionais são equivalentes porque estamos lidando com duas populações com características muito semelhantes. Portanto, a fórmula do intervalo de confiança para a diferença de médias que devemos usar é:
![]()
Assim, calculamos o desvio padrão combinado a partir dos desvios padrão das duas amostras:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
Da mesma forma, devemos encontrar o valor da distribuição t de Student de 80 graus de liberdade com probabilidade de 2,5% na tabela de distribuição de probabilidade da distribuição t de Student :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
Por fim, substituímos os dados na fórmula do intervalo de confiança para a diferença de médias e realizamos os cálculos:
![]()
![]()
![]()
O intervalo de confiança para a diferença nas médias do problema é, portanto, o seguinte:
![]()