Classificação (estatística)

Neste artigo explicamos o que é intervalo nas estatísticas e como ele é calculado. Você encontrará um exercício resolvido sobre o escopo de um conjunto de dados e, por fim, mostraremos para que serve e quando deve ser utilizado.

O que é alcance nas estatísticas?

Nas estatísticas, intervalo é uma medida de dispersão que indica a diferença entre o valor máximo e o valor mínimo dos dados de uma amostra. Portanto, para calcular a extensão de uma população ou amostra estatística, o valor máximo deve ser subtraído do valor mínimo.

Por exemplo, se o valor máximo de um conjunto de dados for 9 e o valor mínimo for 2, o intervalo desta amostra estatística é 7 (9-2=7).

O intervalo estatístico também é chamado de extensão ou intervalo de medição.

Portanto, intervalo é uma medida de dispersão com variância, desvio padrão (ou desvio padrão), desvio médio e coeficiente de variação.

Como calcular o intervalo nas estatísticas

O intervalo de uma amostra é calculado subtraindo os valores extremos dos dados estatísticos da amostra, ou seja , o intervalo de uma amostra é igual ao valor máximo de todos os dados menos o valor mínimo .

Portanto, a fórmula para calcular o intervalo estatístico de um conjunto de dados é:

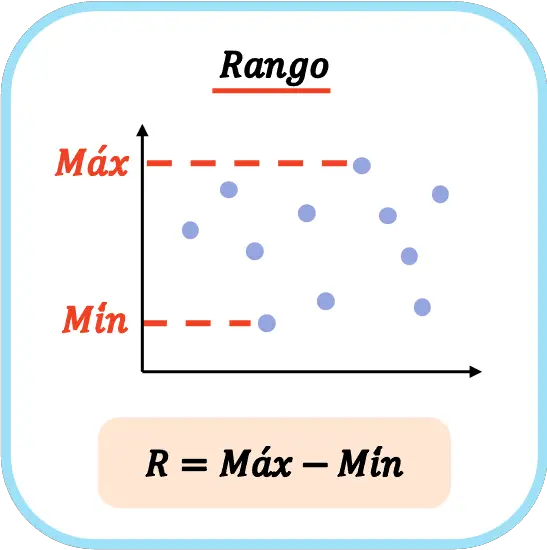
Nas estatísticas, o símbolo de R maiúsculo é frequentemente usado para denotar a extensão de uma série de dados.

Calcular o intervalo de um conjunto de dados é, portanto, bastante simples, pois basta determinar a diferença entre os valores extremos. A única coisa que você precisa prestar atenção é acertar os dados máximos e mínimos e não esquecer nenhum número.

Intervalo de exemplo (estatística)

Depois de ver a definição de intervalo nas estatísticas, abaixo está um exemplo prático para que você possa ver como o intervalo de um conjunto de dados é obtido.

• Uma empresa deseja analisar estatisticamente as vendas alcançadas pelo seu principal produto nos últimos vinte anos. Para fazer isso, eles pedem que você calcule diversas medidas estatísticas, incluindo a classificação. Se as vendas do produto forem as mostradas na tabela a seguir, qual é o alcance desse conjunto de dados?

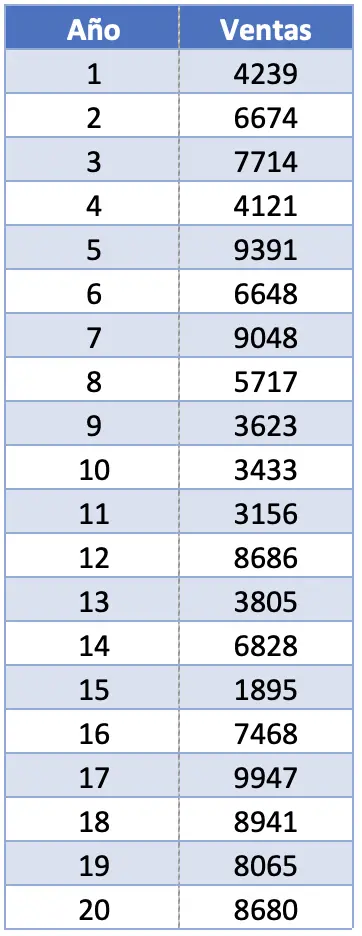
Neste exercício, temos 20 observações. Na realidade, o número total de observações não faz diferença no cálculo da extensão de uma amostra, porque estamos interessados apenas no maior valor e no menor valor.

Devemos, portanto, usar a fórmula vista acima para encontrar a extensão desta amostra estatística.

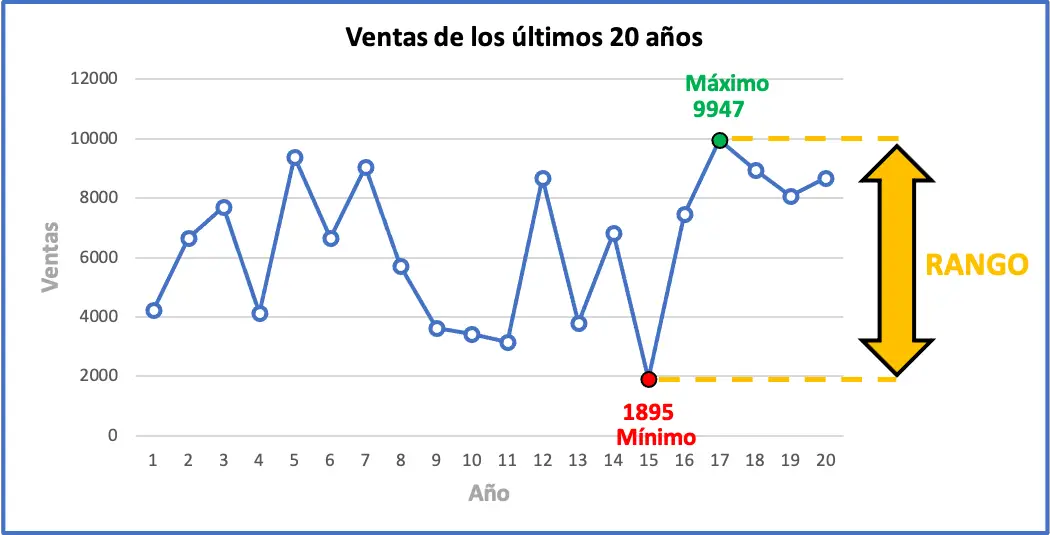
O valor máximo do intervalo é 9.947 unidades vendidas e o valor mínimo é 1.895. Portanto, precisamos subtrair esses dois valores para encontrar o intervalo do conjunto de dados:

Isso significa que a variação máxima nas vendas nos últimos anos é de 8.052 unidades. Abaixo você pode ver graficamente todos os dados do exercício junto com seu intervalo estatístico. O gráfico provavelmente o ajudará a entender o significado do intervalo.

Para que é usado o intervalo estatístico?

Para finalizar a compreensão da noção de extensão nas estatísticas, veremos para que serve e como interpretar esta medida de dispersão.

Nas estatísticas, o intervalo mostra a diferença entre o valor máximo e o valor mínimo de um conjunto de dados. Portanto, intervalo é uma medida usada para indicar a dispersão total de um conjunto de dados .

Quando você conhece o valor do intervalo de um conjunto de dados, você sabe a diferença máxima entre quaisquer duas observações nesse conjunto, para poder ter uma ideia se os dados estão dispersos ou próximos. Em geral, é vantajoso que o alcance seja o mínimo possível, pois isso significa que há pouca dispersão e, portanto, os cálculos serão mais precisos.

Por exemplo, o intervalo pode ser uma medida que permite a comparação entre duas amostras diferentes, pois permite ter uma ideia das dispersões das amostras.

No entanto, deve-se ter cautela na interpretação do intervalo estatístico, pois pode ser enganoso. Pode ser que um conjunto de dados tenha realmente uma dispersão muito baixa, mas se houver um valor atípico na amostra, o intervalo será muito amplo e, portanto, não refletirá adequadamente a dispersão da amostra.

Além disso, não é a mesma coisa que uma amostra cujos valores são da ordem das dezenas tenha a classificação 5, e uma amostra cujos valores são da ordem dos milhares tenha a mesma classificação. Logicamente, mesmo que ambas as faixas tenham o mesmo número, a primeira amostra é muito mais dispersa que a segunda.

Concluindo, o intervalo é uma medida estatística útil para analisar a dispersão de um conjunto de dados, mas para interpretar corretamente os dados, outras métricas também devem ser calculadas.