Como calcular intervalos de confiança no excel
Um intervalo de confiança é um intervalo de valores que provavelmente contém um parâmetro populacional com um certo nível de confiança. É calculado de acordo com a seguinte fórmula geral:
Intervalo de confiança = (estimativa pontual) +/- (valor crítico)* (erro padrão)
Esta fórmula cria um intervalo com um limite inferior e um limite superior, que provavelmente contém um parâmetro populacional com algum nível de confiança:
Intervalo de confiança = [limite inferior, limite superior]
Este tutorial explica como calcular os seguintes intervalos de confiança no Excel:
1. Intervalo de confiança para uma média
2. Intervalo de confiança para diferença de médias
3. Intervalo de confiança para uma proporção
4. Intervalo de confiança para diferença de proporções
Vamos!
Exemplo 1: Intervalo de confiança para uma média
Usamos a seguinte fórmula para calcular um intervalo de confiança para uma média :
Intervalo de confiança = x +/- z*(s/√n)
Ouro:
- x : médias amostrais
- z: o valor z escolhido
- s: desvio padrão da amostra
- n: tamanho da amostra
Exemplo: Suponha que coletamos uma amostra aleatória de tartarugas com as seguintes informações:
- Tamanho da amostra n = 25
- Peso médio da amostra x = 300
- Desvio padrão amostral s = 18,5
A captura de tela a seguir mostra como calcular um intervalo de confiança de 95% para o peso médio real da população de tartarugas:
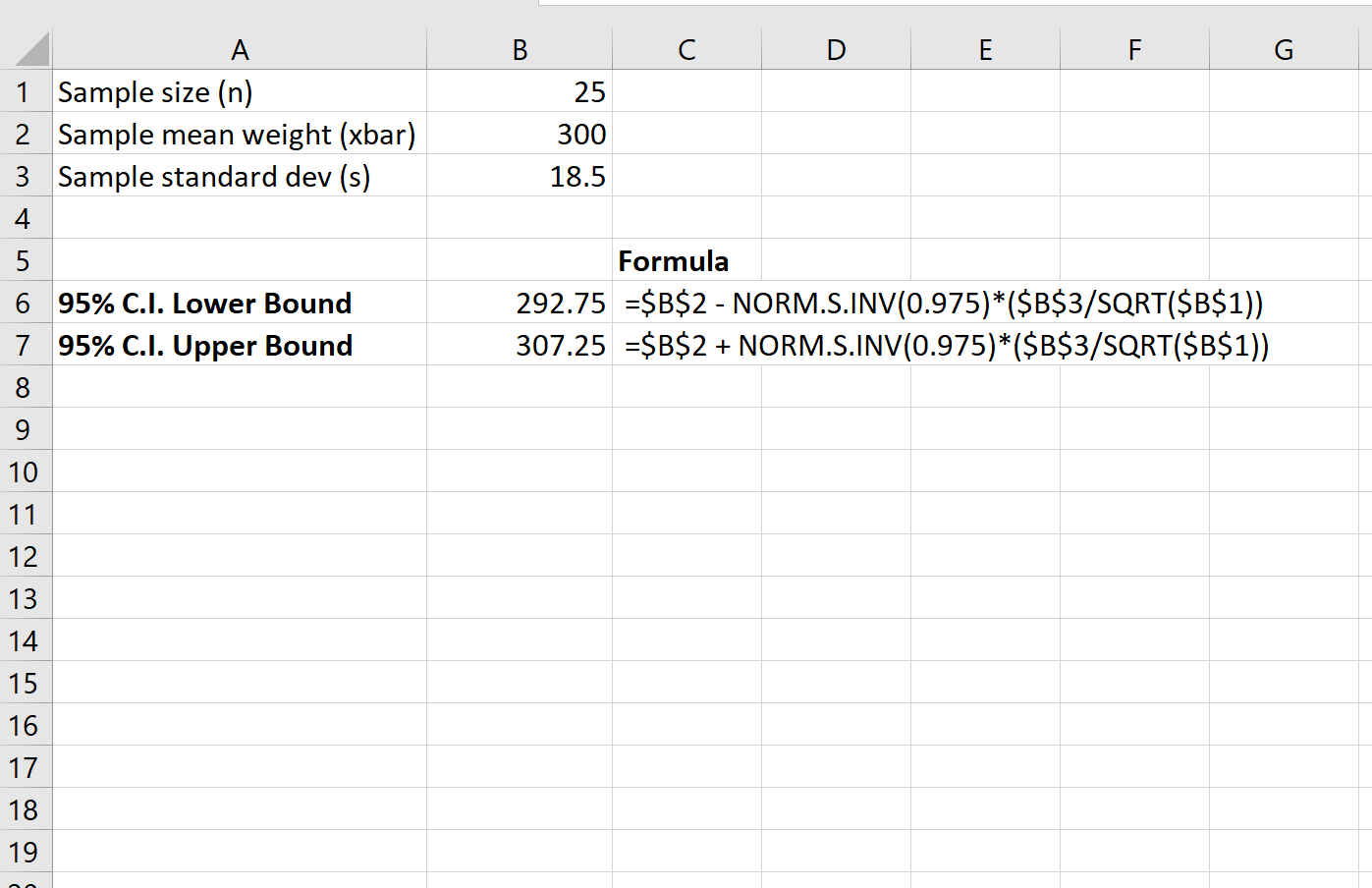
O intervalo de confiança de 95% para o verdadeiro peso médio da população de tartarugas é [292,75, 307,25] .
Exemplo 2: Intervalo de confiança para diferença de médias
Usamos a seguinte fórmula para calcular um intervalo de confiança para uma diferença nas médias populacionais :
Intervalo de confiança = ( x 1 – x 2 ) +/- t*√((s p 2 /n 1 ) + (s p 2 /n 2 ))
Ouro:
- x 1 , x 2 : média da amostra 1, média da amostra 2
- t: o valor t-crítico baseado no nível de confiança e (n 1 + n 2 -2) graus de liberdade
- s p 2 : variância combinada, calculada como ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
- t: o valor t-crítico
- n 1 , n 2 : tamanho da amostra 1, tamanho da amostra 2
Exemplo: Suponha que queiramos estimar a diferença no peso médio entre duas espécies diferentes de tartarugas. Portanto, coletamos uma amostra aleatória de 15 tartarugas de cada população. Aqui estão os dados resumidos para cada amostra:
Amostra 1:
- x1 = 310
- s 1 = 18,5
- n 1 = 15
Amostra 2:
- x2 = 300
- s2 = 16,4
- n2 = 15
A captura de tela a seguir mostra como calcular um intervalo de confiança de 95% para a verdadeira diferença nas médias populacionais:
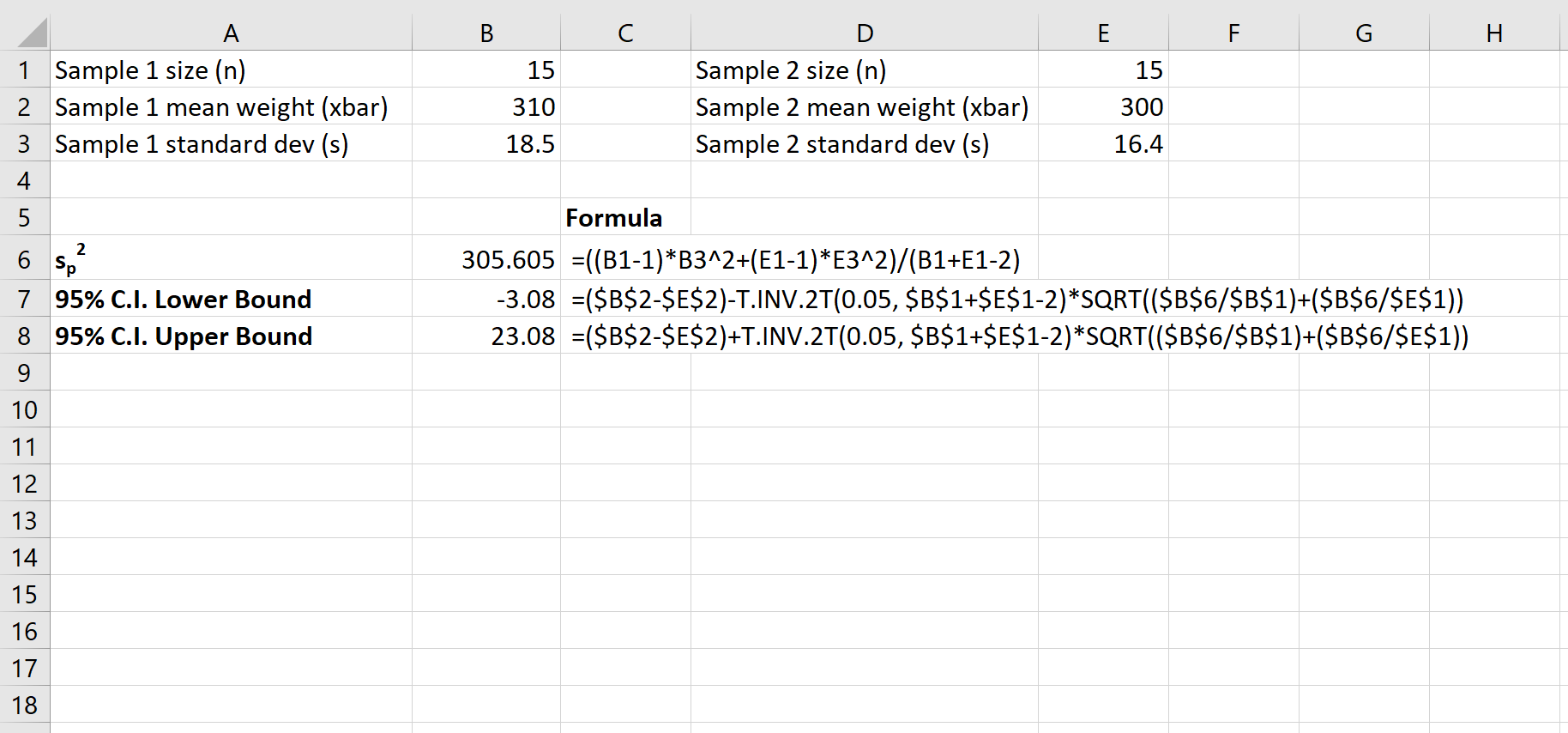
O intervalo de confiança de 95% para a verdadeira diferença entre as médias da população é [-3,08, 23,08] .
Exemplo 3: Intervalo de confiança para uma proporção
Usamos a seguinte fórmula para calcular um intervalo de confiança para uma proporção :
Intervalo de confiança = p +/- z*√ p(1-p) / n
Ouro:
- p: proporção da amostra
- z: o valor z escolhido
- n: tamanho da amostra
Exemplo: Suponha que queiramos estimar a proporção de residentes num condado que são a favor de uma determinada lei. Selecionamos uma amostra aleatória de 100 residentes e perguntamos qual é a sua posição em relação à lei. Aqui estão os resultados:
- Tamanho da amostra n = 100
- Proporção a favor da lei p = 0,56
A captura de tela a seguir mostra como calcular um intervalo de confiança de 95% para a verdadeira proporção de residentes em todo o condado que são a favor da lei:
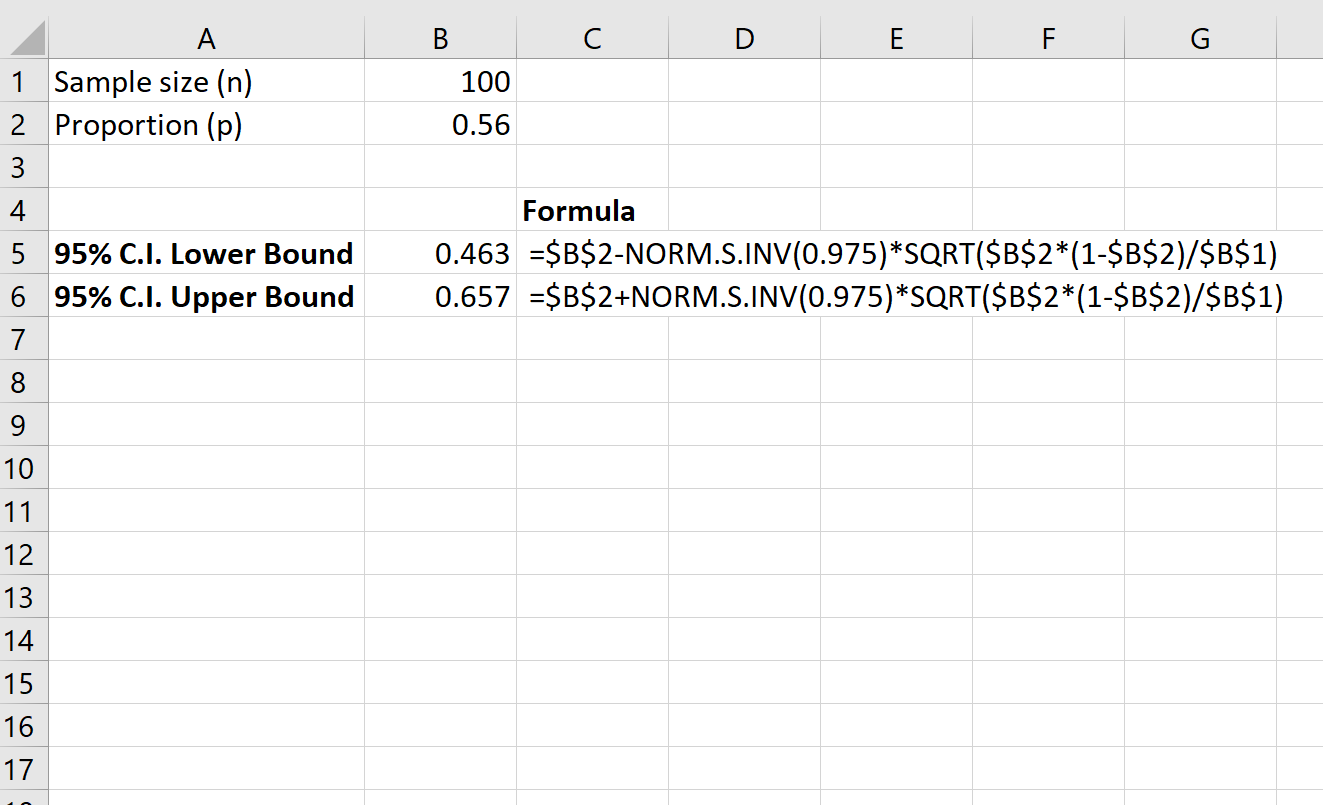
O intervalo de confiança de 95% para a verdadeira proporção de residentes em todo o condado que são a favor da lei é [0,463, 0,657] .
Exemplo 4: Intervalo de confiança para diferença de proporções
Usamos a seguinte fórmula para calcular um intervalo de confiança para uma diferença em proporções :
Intervalo de confiança = (p 1 –p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )
Ouro:
- p 1 , p 2 : proporção da amostra 1, proporção da amostra 2
- z: o valor crítico z com base no nível de confiança
- n 1 , n 2 : tamanho da amostra 1, tamanho da amostra 2
Exemplo: Suponha que queremos estimar a diferença entre a proporção de residentes que apoiam uma determinada lei no condado A em comparação com a proporção que apoia a lei no condado B. Aqui estão os dados resumidos para cada amostra:
Amostra 1:
- n 1 = 100
- p 1 = 0,62 (ou seja, 62 habitantes em cada 100 apoiam a lei)
Amostra 2:
- n2 = 100
- p 2 = 0,46 (ou seja, 46 habitantes em cada 100 apoiam a lei)
A captura de tela a seguir mostra como calcular um intervalo de confiança de 95% para a verdadeira diferença na proporção de residentes que apoiam a lei entre condados:
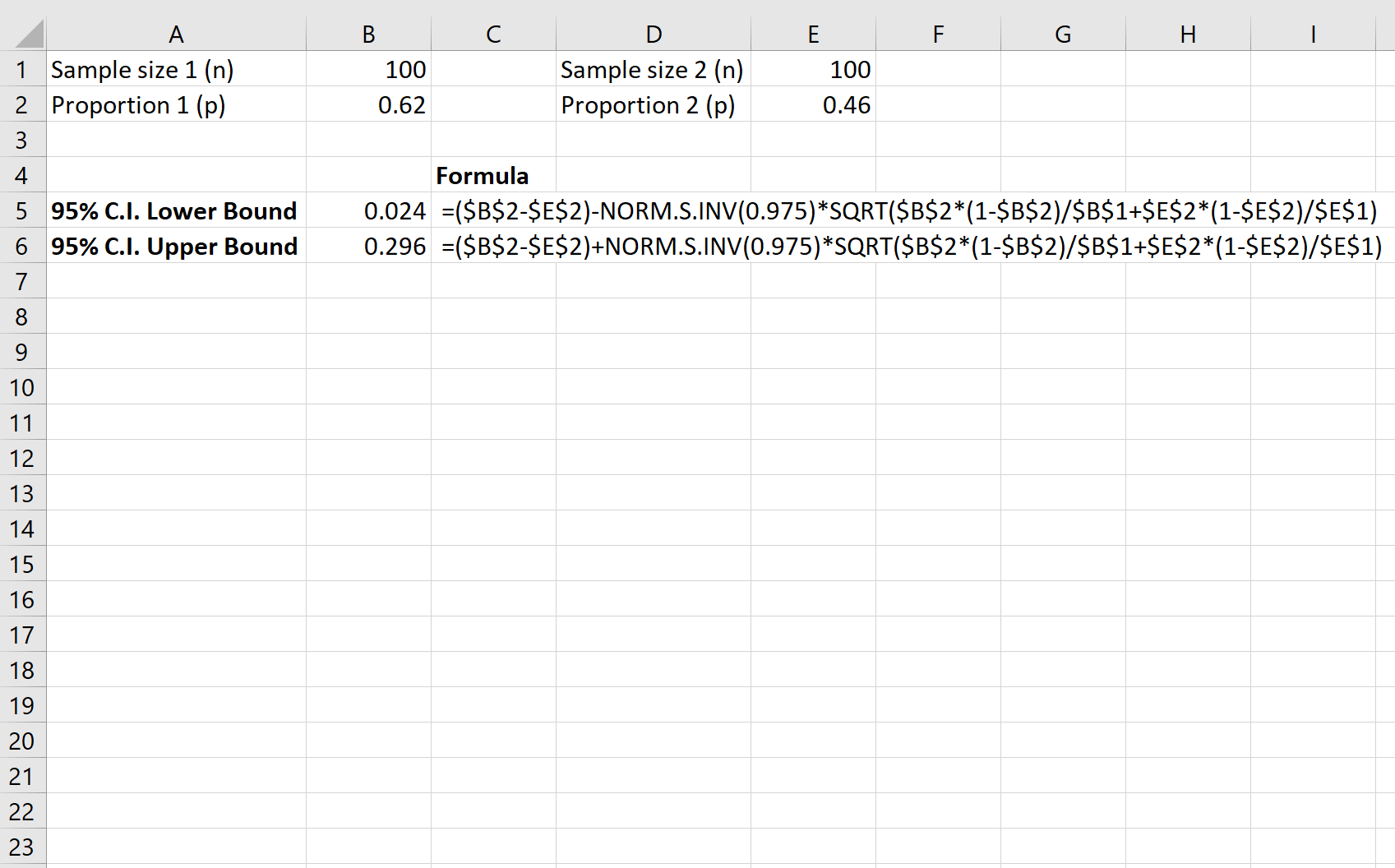
O intervalo de confiança de 9,5% para a verdadeira diferença na proporção de residentes que apoiam a lei entre condados é [0,024, 0,296] .
Você pode encontrar mais tutoriais de Excel aqui .
About Author
Dr. benjamim anderson
Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais