Tau de kendall: definição + exemplo

Nas estatísticas, a correlação refere-se à força e à direção de uma relação entre duas variáveis. O valor de um coeficiente de correlação pode variar de -1 a 1, com -1 indicando um relacionamento negativo perfeito, 0 indicando nenhum relacionamento e 1 indicando um relacionamento positivo perfeito.

O coeficiente de correlação mais comumente utilizado é o coeficiente de correlação de Pearson , que mede a associação linear entre duas variáveis numéricas.

Um coeficiente de correlação menos comumente usado é o Tau de Kendall , que mede a relação entre duas colunas de dados classificados.

A fórmula para calcular o Tau de Kendall, frequentemente abreviado como τ, é a seguinte:

τ = (CD) / (C+D)

Ouro:

C = o número de pares correspondentes

D = o número de pares discordantes

O exemplo a seguir ilustra como usar esta fórmula para calcular o coeficiente de correlação de classificação Tau de Kendall para duas colunas de dados classificados.

Exemplo de cálculo do Tau de Kendall

Supõe que dois treinadores de basquete classifiquem 12 de seus jogadores, do pior ao melhor. A tabela a seguir mostra as classificações que cada treinador atribuiu aos jogadores:

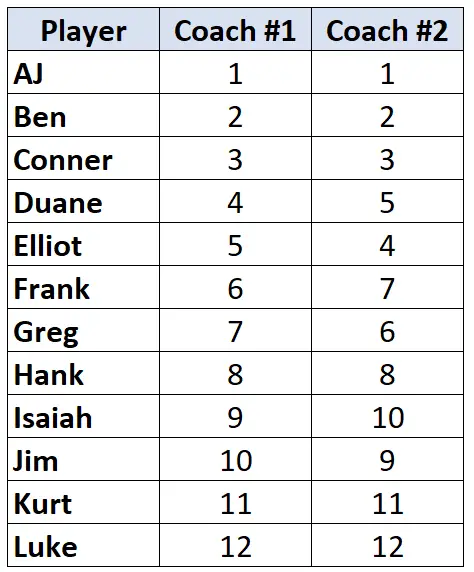
Como estamos trabalhando com duas colunas de dados classificados, é apropriado utilizar o Tau de Kendall para calcular a correlação entre as classificações dos dois treinadores. Siga as seguintes etapas para calcular o Tau de Kendall:

Etapa 1: conte o número de pares correspondentes.

Veja apenas as classificações do treinador nº 2. Começando pelo primeiro jogador, conte quantos níveis abaixo dele são mais altos . Por exemplo, existem 11 números abaixo de “1” que são maiores, então escreveremos 11:

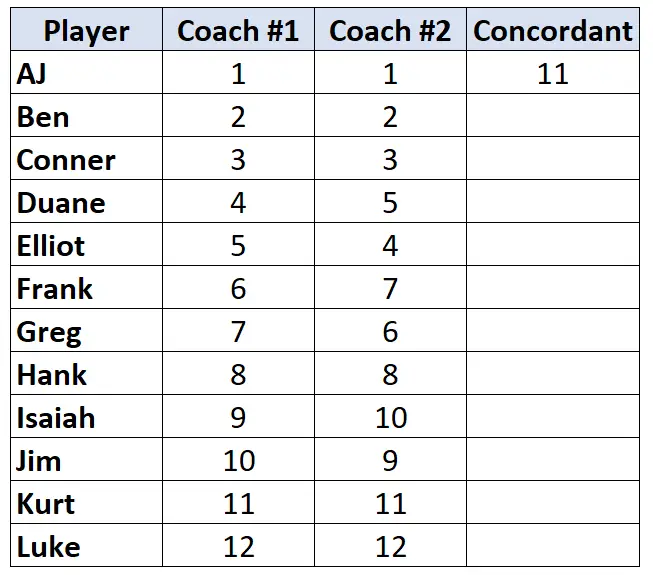
Passe para o próximo jogador e repita o processo. Existem 10 números abaixo de “2” que são maiores, então escreveremos 10:

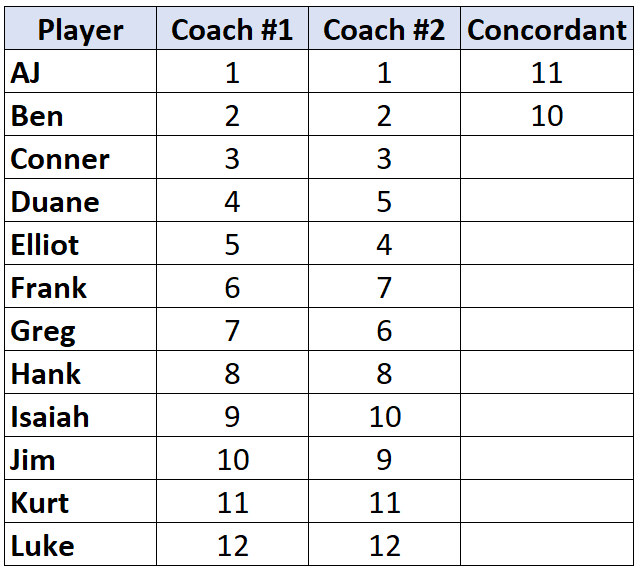
Quando alcançamos um jogador cuja classificação é inferior à do jogador anterior, ele simplesmente recebe o mesmo valor do jogador anterior. Por exemplo, Elliot tem uma classificação de “4” que é inferior à classificação de “5” do jogador anterior, então ele simplesmente recebe o mesmo valor que o jogador antes dele:

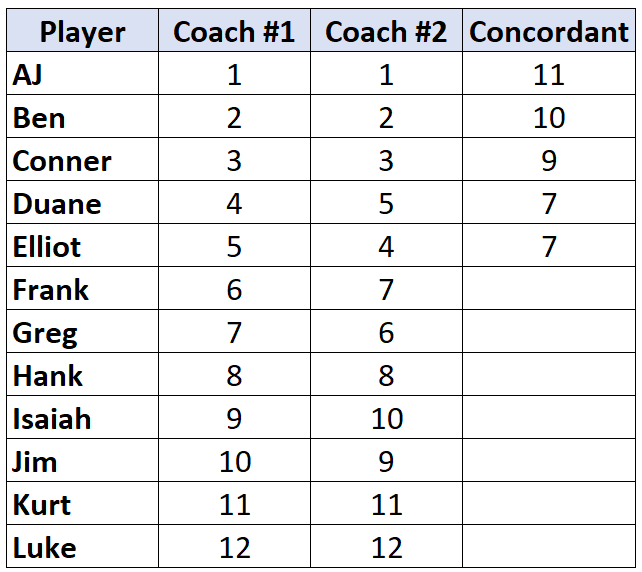
Repita este processo para todos os jogadores:

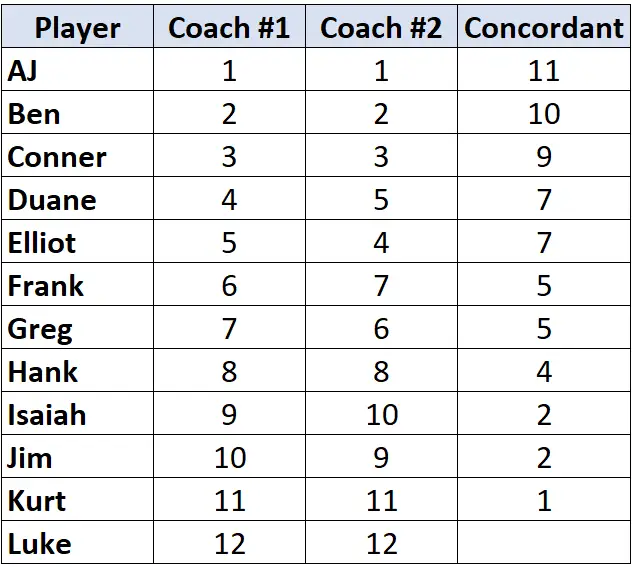
Etapa 2: conte o número de pares discordantes.

Novamente, observe apenas as classificações do treinador nº 2. Para cada jogador, conte quantas fileiras abaixo dele são menores . Por exemplo, o treinador nº 2 atribuiu a AJ a classificação “1” e nenhum jogador abaixo dele tem uma classificação inferior. Assim, atribuímos a ele o valor 0:

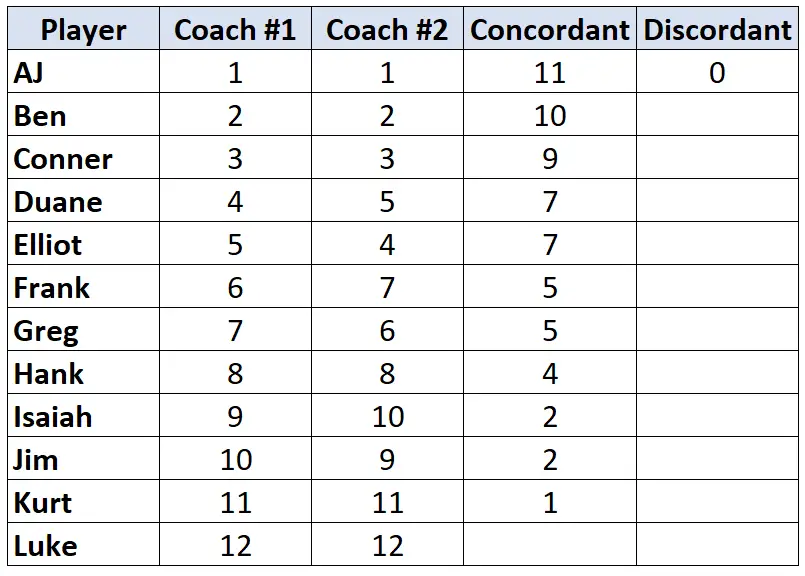
Repita este processo para cada jogador:

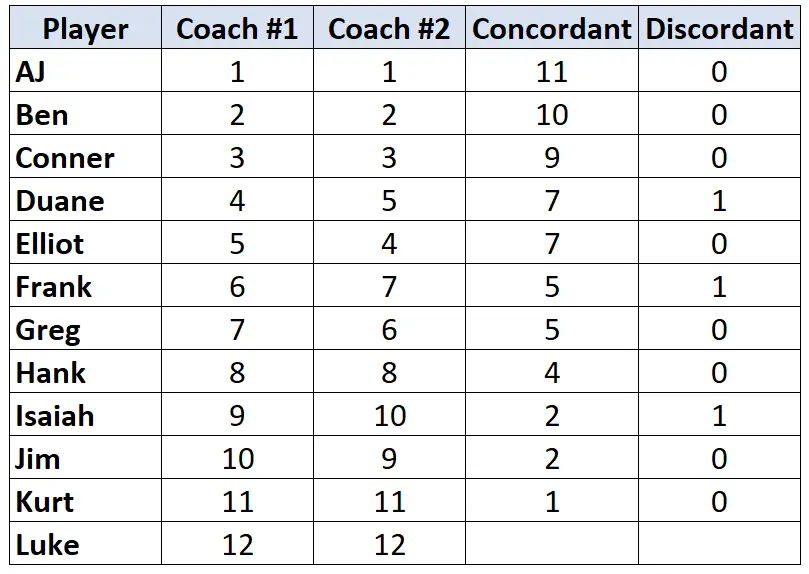
Etapa 3: Calcule a soma de cada coluna e encontre o Tau de Kendall.

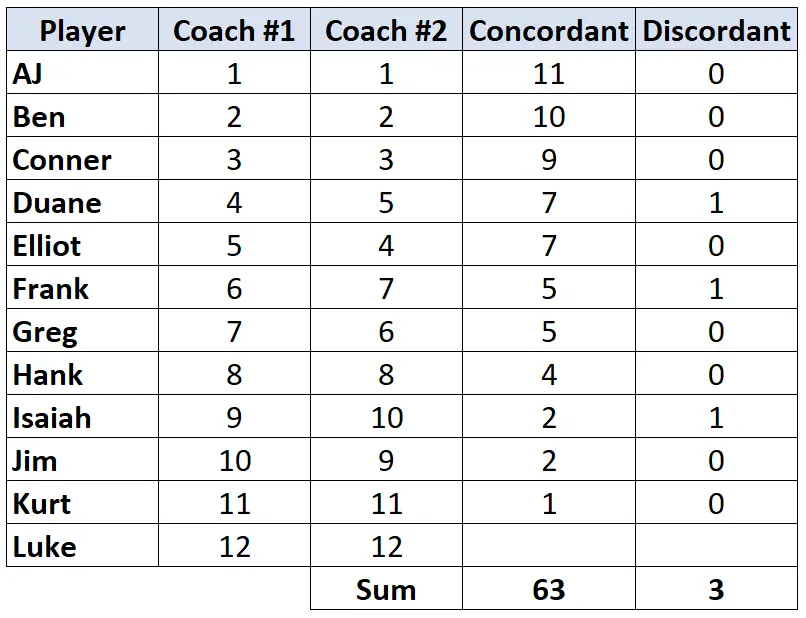
Tau de Kendall = (CD) / (C+D) = (63-3) / (63+3) = (60/66) = 0,909 .

Importância estatística do Tau de Kendall

Quando você tem mais de n=10 pares, o Tau de Kendall geralmente segue uma distribuição normal. Você pode usar a seguinte fórmula para calcular uma pontuação z para o Tau de Kendall:

z = 3τ*√ n(n-1) / √ 2(2n+5)

Ouro:

τ = valor que você calculou para o Tau de Kendall

n = número de pares

Veja como calcular z para o exemplo anterior:

z = 3(0,909)*√ 12(12-1) / √ 2(2*12+5) = 4,11 .

Usando a calculadora de pontuação Z do valor P, vemos que o valor p para essa pontuação z é 0,00004 , o que é estatisticamente significativo no nível alfa de 0,05. Assim, existe uma correlação estatisticamente significativa entre as classificações que os dois treinadores atribuíram aos jogadores.

Bônus: como calcular o Tau de Kendall em R

No software de estatística R, você pode usar a função kendall.tau() da biblioteca VGAM para calcular o Tau de Kendall para dois vetores, que usa a seguinte sintaxe:

kendall.tau(x, y)

onde x e y são dois vetores digitais de igual comprimento.

O código a seguir ilustra como calcular o Tau de Kendall para os dados exatos que usamos no exemplo anterior:

 #load VGAM
library(VGAM)

#create vector for each coach's rankings
coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12)
coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12)

#calculate Kendall's Tau
kendall.tau(coach_1, coach_2)

#[1] 0.9090909

Observe como o valor Tau de Kendall corresponde ao valor que calculamos manualmente.