Lei da probabilidade total: definição e exemplos

Na teoria das probabilidades, a lei da probabilidade total é uma forma útil de determinar a probabilidade de um evento A quando não conhecemos diretamente a probabilidade de A , mas sabemos que os eventos B ₁ , B ₂ , B ₃ … formam uma partição. do espaço amostral S.

Esta lei especifica o seguinte:

A lei da probabilidade total

Se B ₁ , B ₂ , B ₃ … formam uma partição do espaço amostral S , então podemos calcular a probabilidade do evento A da seguinte forma:

P( A ) = ΣP( A | Bi ₎ *P( Bi ₎

A maneira mais fácil de entender esta lei é tomar um exemplo simples.

Suponha que haja dois sacos em uma caixa contendo as seguintes bolinhas de gude:

• Saco 1: 7 bolinhas vermelhas e 3 bolinhas verdes
• Saco 2: 2 bolinhas vermelhas e 8 bolinhas verdes

Se selecionarmos aleatoriamente um dos sacos e, em seguida, selecionarmos aleatoriamente uma bola de gude desse saco, qual é a probabilidade de que seja uma bola de gude verde?

Neste exemplo, seja P( G ) = probabilidade de escolher uma bola de gude verde. É a probabilidade que nos interessa, mas não podemos calculá-la diretamente.

Em vez disso, precisamos usar a probabilidade condicional de G , dado algum evento B onde o B _i forma uma partição do espaço amostral S. Neste exemplo, temos as seguintes probabilidades condicionais:

• P(G| _B1 ) = 3/10 = 0,3
• P(G| _B2 ) = 8/10 = 0,8

Assim, usando a lei da probabilidade total, podemos calcular a probabilidade de escolher uma bola de gude verde da seguinte forma:

• P(G) = ΣP(G|B _i )*P(B _i )
• P(G) = P(G|B ₁ )*P(B ₁ ) + P(G|B ₂ )*P(B ₂ )
• P(G) = (0,3)*(0,5) + (0,8)*(0,5)
• P(G) = 0,55

Se selecionarmos aleatoriamente um dos sacos e, em seguida, selecionarmos aleatoriamente uma bola de gude desse saco, a probabilidade de escolhermos uma bola de gude verde é de 0,55 .

Leia os dois exemplos a seguir para solidificar sua compreensão da lei da probabilidade total.

Exemplo 1: Widgets

A empresa A fornece 80% dos widgets para uma oficina de automóveis e apenas 1% de seus widgets apresenta defeito. A empresa B fornece os 20% restantes dos widgets para a oficina mecânica e 3% de seus widgets apresentam defeito.

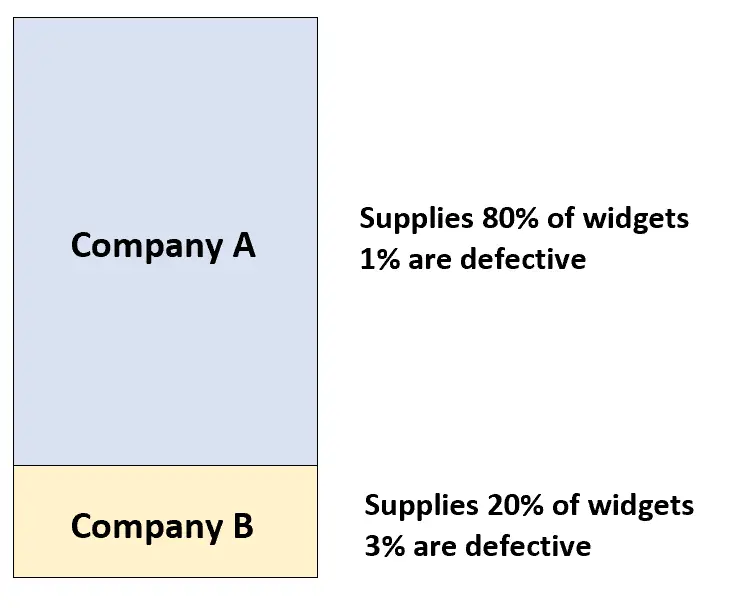
Se um cliente comprar aleatoriamente um widget em uma oficina mecânica, qual é a probabilidade de ele estar com defeito?

Se deixarmos P( D ) = a probabilidade de um widget estar com defeito e P(B _i ) a probabilidade de o widget vir de uma das empresas, então podemos calcular a probabilidade de comprar um widget com defeito da seguinte forma:

• P(D) = ΣP(D|B _i )*P(B _i )
• P(D) = P(D|B ₁ )*P(B ₁ ) + P(D|B ₂ )*P(B ₂ )
• P(D) = (0,01)*(0,80) + (0,03)*(0,20)
• P(D) = 0,014

Se comprarmos aleatoriamente um widget nesta loja de automóveis, a probabilidade de ele estar com defeito é 0,014 .

Exemplo 2: Florestas

A Floresta A ocupa 50% da área total de um determinado parque, e 20% das plantas desta floresta são venenosas. A Floresta B ocupa 30% da área total e 40% das plantas que contém são venenosas. A Floresta C ocupa os 20% restantes do território e 70% das plantas ali encontradas são venenosas.

Se entrarmos aleatoriamente neste parque e colhermos uma planta do chão, qual a probabilidade de ela ser venenosa?

Se deixarmos P( P ) = a probabilidade de a planta ser venenosa, e P(B _i ) a probabilidade de termos entrado em uma das três florestas, então podemos calcular a probabilidade de uma planta escolhida aleatoriamente ser tóxica como:

• P(P) = ΣP(P|B _i )*P(B _i )
• P(P) = P(P|B ₁ )*P(B ₁ ) + P(P|B ₂ )*P(B ₂ ) + P(P|B ₃ )*P(B ₃ )
• P(P) = (0,20)*(0,50) + (0,40)*(0,30) + (0,70)*(0,20)
• P(P) = 0,36

Se escolhermos aleatoriamente uma planta do solo, a probabilidade de ela ser tóxica é de 0,36 .

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre tópicos de probabilidade:

Como encontrar a média de uma distribuição de probabilidade
Como encontrar o desvio padrão de uma distribuição de probabilidade
Calculadora de distribuição de probabilidade