Distribuição de pareto
Este artigo explica o que é a distribuição de Pareto nas estatísticas e para que ela é usada. Você também poderá ver o gráfico da distribuição de Pareto e as propriedades desse tipo de distribuição de probabilidade.
O que é distribuição de Pareto?
A distribuição de Pareto é uma distribuição de probabilidade contínua usada em estatística para modelar o princípio de Pareto. Portanto, a distribuição de Pareto é uma distribuição de probabilidade que possui alguns valores cuja probabilidade de ocorrência é muito maior que o restante dos valores.
Lembre-se que a lei de Pareto, também chamada de regra 80-20, é um princípio estatístico que diz que a maior parte da causa de um fenômeno se deve a uma pequena parte da população.
A distribuição de Pareto possui dois parâmetros característicos: o parâmetro de escala x m e o parâmetro de forma α.
Originalmente, a distribuição de Pareto era usada para descrever a distribuição da riqueza dentro da população, porque a maior parte dela se devia a uma pequena proporção da população. Mas actualmente a distribuição de Pareto tem muitas aplicações, por exemplo no controlo de qualidade, na economia, na ciência, no campo social, etc.
A distribuição de Pareto leva o nome do economista Vilfredo Pareto, que formulou a distribuição. No entanto, ele é mais conhecido pelo gráfico de Pareto.
Tabela de distribuição de Pareto
Agora que conhecemos a definição de distribuição de Pareto, vejamos vários exemplos de distribuições de Pareto representadas graficamente.
Assim, a seguir você pode ver como fica o gráfico da função densidade da distribuição de Pareto dependendo de seus valores característicos:
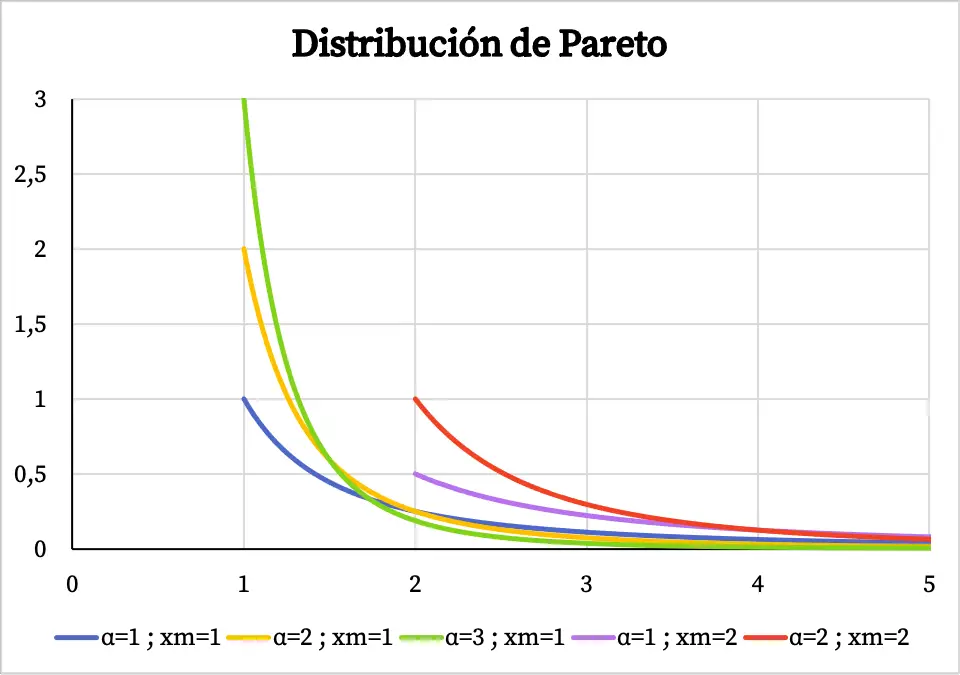
Observe que o domínio da distribuição de Pareto vai do valor x m até +∞, razão pela qual a função densidade não existe antes do valor de x m .
Por outro lado, o gráfico da função de probabilidade cumulativa da distribuição de Pareto é o seguinte:
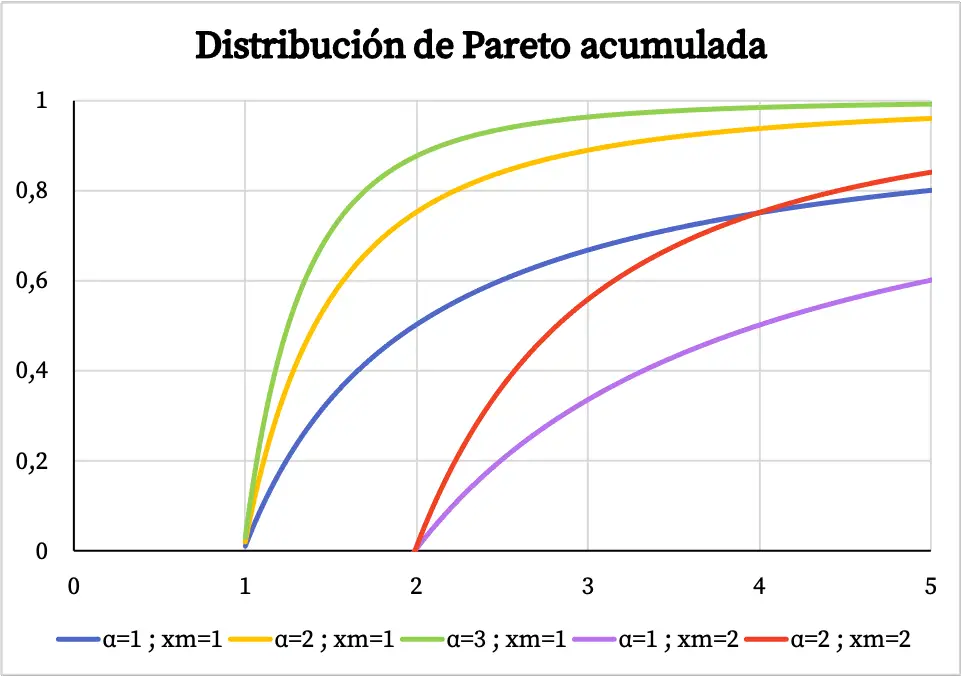
Características da distribuição de Pareto
Abaixo estão as características mais importantes da distribuição de Pareto relacionadas à teoria de probabilidade e estatística.
- A distribuição de Pareto possui dois parâmetros característicos que definem sua curva: o parâmetro de escala x m e o parâmetro de forma α.
- O domínio da distribuição de Pareto consiste em todos os números reais desde o parâmetro de escala até mais o infinito.
- Se α for maior que 1, a média da distribuição de Pareto é igual ao produto de α vezes x m e α menos 1.
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”34″ width=”214″ style=”vertical-align: -12px;”></p>
</p>
<ul>
<li> A variância da distribuição de Pareto depende dos dois parâmetros característicos da distribuição e é calculada com a seguinte fórmula:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6d26513868f9ed6fa45ab0fde0030884_l3.png)
![\displaystyle Me=x_\mathrm{m}\cdot \sqrt[\alpha]{2}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0dc2c772a0a0662ad05f8b22c3cf1ba1_l3.png "Rendered by QuickLaTeX.com")
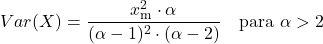
- A moda da distribuição de Pareto é equivalente ao parâmetro de escala x m da distribuição.
- A fórmula para a função densidade da distribuição de Pareto é:
![\displaystyle P[X=x]=\frac{\alpha\cdot x_m^\alpha}{x^{\alpha+1}}\quad\text{para }x\geq x_m](https://statorials.org/wp-content/ql-cache/quicklatex.com-1e182771cfe3bf9a145a2ee59b9c7eeb_l3.png "Rendered by QuickLaTeX.com")
- Da mesma forma, a fórmula para a função de probabilidade cumulativa da distribuição de Pareto é:
![\displaystyle P[X\leq x]=1-\left(\frac{x_\mathrm{m}}{x}\right)^\alpha](https://statorials.org/wp-content/ql-cache/quicklatex.com-480adc7841b7c72cb4bfecb446ed3fab_l3.png "Rendered by QuickLaTeX.com")
- O coeficiente de assimetria da distribuição de Pareto depende apenas do parâmetro de forma α e sua expressão é:
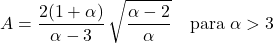
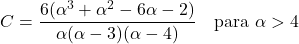
About Author
Dr. benjamim anderson
Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais