Lei dos grandes números: definição + exemplos

A lei dos grandes números afirma que à medida que o tamanho de uma amostra aumenta, a média amostral se aproxima do valor esperado.

O exemplo mais básico é jogar uma moeda. Cada vez que jogamos uma moeda, a probabilidade de dar cara é 1/2. Portanto, a proporção esperada de caras que aparecerão em um número infinito de lançamentos é 1/2 ou 0,5 .

No entanto, se lançarmos uma moeda 10 vezes, poderemos descobrir que ela só dá cara 3 vezes. Como 10 lançamentos é um tamanho de amostra pequeno, não há garantia de que a proporção da cabeça será próxima de 0,5 .

Se continuarmos a lançar a moeda mais 10 vezes, poderemos descobrir que ela dá cara um total de 9 em 20 vezes. Se a lançarmos mais 10 vezes, podemos descobrir que ela dá cara 22 em 30 vezes.

À medida que lançamos a moeda, a proporção de vezes que ela dá cara convergirá para a proporção esperada de 0,5 .

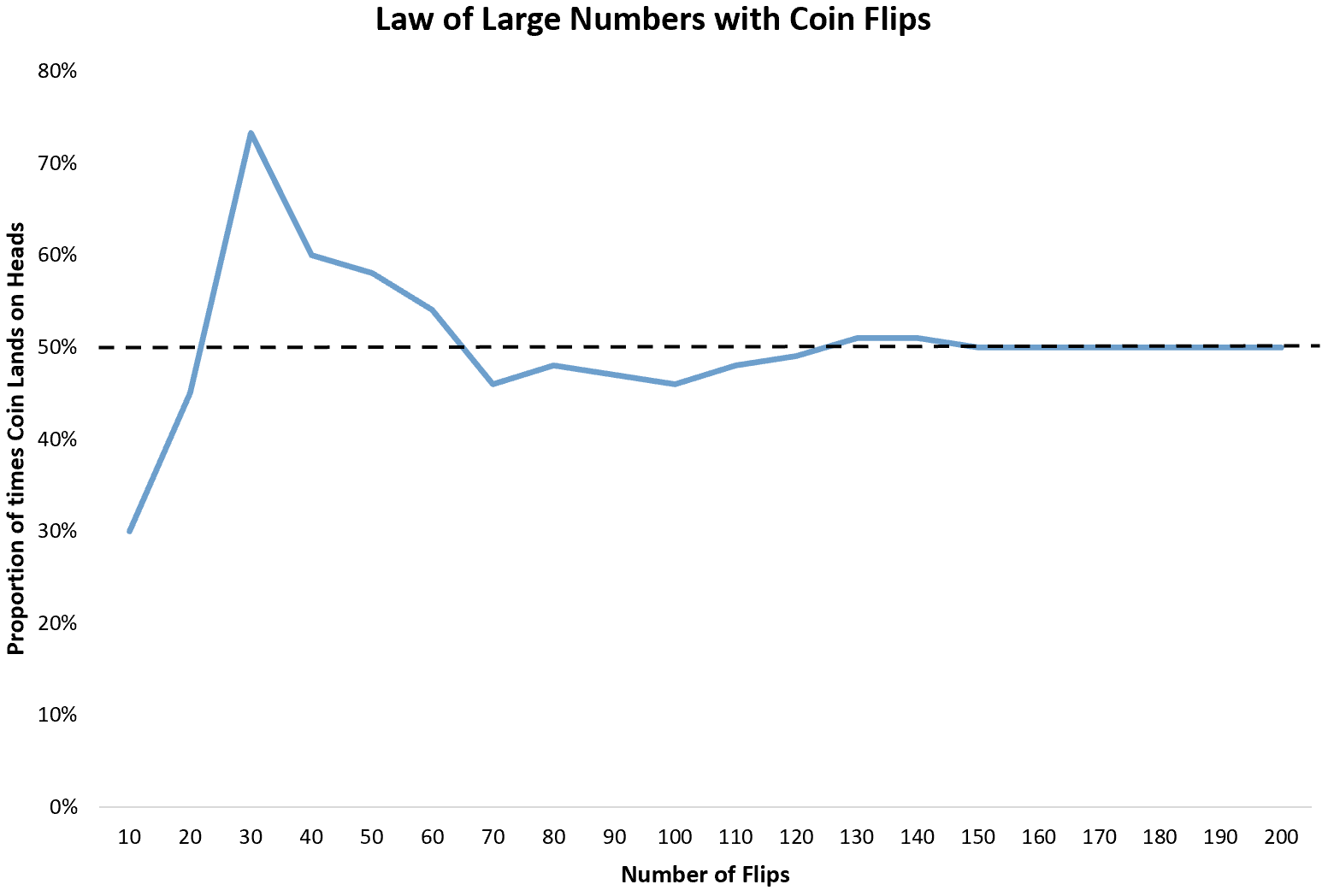
Essa ideia simples da lei dos grandes números é aplicada por muitos tipos de empresas e indústrias na vida real.

A lei dos grandes números nos cassinos

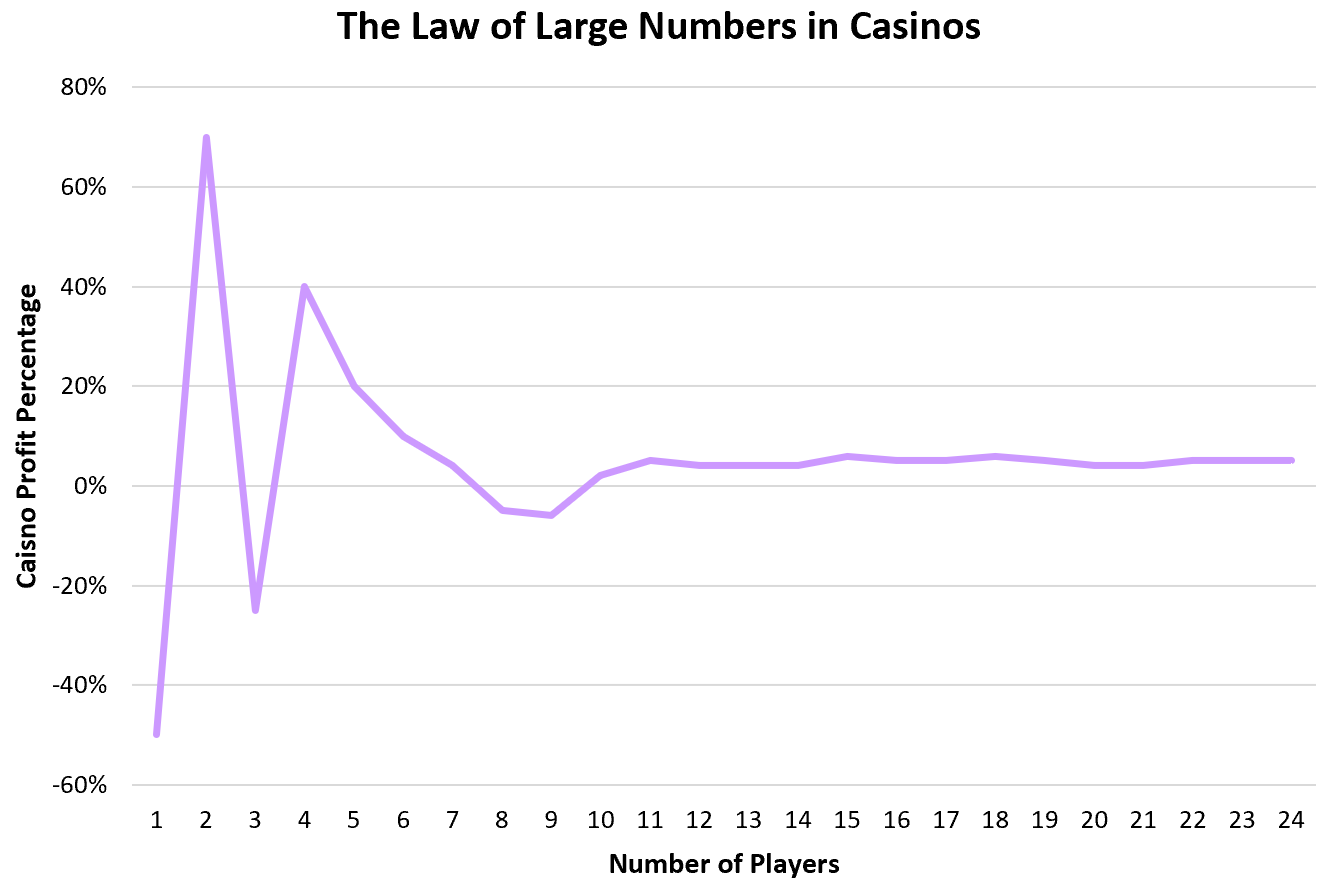
Os cassinos contam com a lei dos grandes números para gerar lucros de forma confiável. Para a maioria dos jogos, o casino ganha cerca de 51-55% das vezes. Isto significa que os indivíduos podem ter sorte e ganhar uma quantia decente de vez em quando, mas entre dezenas de milhares de jogadores individuais, o casino ganhará o esperado 51-55% das vezes.

Por exemplo, Jéssica poderia jogar alguns jogos no cassino e ganhar US$ 50.

Mike também poderia jogar alguns jogos e perder $70.

John poderia jogar alguns jogos e ganhar $25.

Susan poderia jogar alguns jogos e perder $40.

Alguns jogadores ganharão dinheiro e outros perderão dinheiro, mas devido à forma como os jogos são concebidos, os casinos podem ter a certeza de que ganharão entre milhares de indivíduos.

A lei dos grandes números em seguros

As companhias de seguros também dependem da lei dos grandes números para permanecerem lucrativas.

A ideia básica é que milhares de companhias de seguros podem fornecer seguro a pessoas que pagam um determinado prémio todos os meses e que apenas uma pequena percentagem das pessoas que seguram necessitarão realmente de utilizar o seguro para pagar grandes despesas inesperadas.

Por exemplo, 1.000 pessoas poderiam pagar cada uma US$ 1.000 por ano por seguros, o que geraria um lucro de US$ 1.000.000 para uma seguradora.

No entanto, 90 pessoas podem precisar receber, cada uma, US$ 10.000 da seguradora para cobrir despesas inesperadas relacionadas a vários acidentes, resultando em uma perda de US$ 900.000 para a seguradora.

No final, a seguradora obtém um lucro de US$ 1.000.000 – US$ 900.000 = US$ 100.000 .

Isto significa que a seguradora pode esperar obter um lucro bastante previsível, em média, sobre milhares de pessoas.

Observe que esse modelo econômico funciona porque uma seguradora segura um grande número de pessoas . Se eles segurassem apenas 10 pessoas, seria muito arriscado porque uma grande despesa inesperada poderia acabar com o negócio.

Assim, as companhias de seguros baseiam-se na lei dos grandes números para prever os seus lucros de uma forma previsível.

A lei dos grandes números nas energias renováveis

A lei dos grandes números também é utilizada por empresas de energia renovável.

A ideia básica é que turbinas eólicas e painéis solares possam alimentar geradores para produzir eletricidade em diferentes partes do negócio. No entanto, não há vento nem sol lá fora, o que significa que as turbinas eólicas e os painéis solares nem sempre são capazes de produzir energia confiável para geradores elétricos.

A forma como as empresas de energia renovável contornam este problema é ligar dezenas de milhares de turbinas eólicas ou painéis solares a uma única rede eléctrica, tornando muito mais provável que estas fontes de energia produzam uma quantidade fiável de energia. energia para a rede.

Também é muito mais fácil prever quanta energia será produzida por estas fontes de energia, uma vez que os engenheiros podem simplesmente calcular a média esperada de dezenas de milhares de turbinas eólicas ou painéis solares.

Uma explicação detalhada deste fenômeno pode ser encontrada neste artigo da Scientific American .