Teste u de mann-whitney
Um teste U de Mann-Whitney (às vezes chamado de teste de soma de postos de Wilcoxon) é usado para comparar diferenças entre duas amostras independentes quando as distribuições amostrais não são normalmente distribuídas e os tamanhos das amostras são pequenos (n <30).
É considerado o equivalente não paramétrico do teste t independente para duas amostras .
Aqui estão alguns exemplos de quando você pode usar um teste U de Mann-Whitney:
- Você deseja comparar os salários de cinco graduados da universidade A com os salários de cinco graduados da universidade B. Os salários não são distribuídos normalmente.
- Você quer saber se a perda de peso varia para dois grupos: 12 pessoas que usam a dieta A e 10 pessoas que usam a dieta B. A perda de peso não é normalmente distribuída.
- Você quer saber se as notas de 8 alunos da turma A diferem daquelas de 7 alunos da turma B. As notas não são distribuídas normalmente.
Em cada exemplo, você deseja comparar dois grupos, as distribuições amostrais não são normais e os tamanhos amostrais são pequenos.
Assim, um teste U de Mann-Whitney é apropriado desde que as seguintes suposições sejam atendidas.
Suposições do teste Mann-Whitney U
Antes de realizar um teste U de Mann-Whitney, você deve garantir que as quatro suposições a seguir sejam atendidas:
- Ordinária ou contínua: A variável que você está analisando é ordinal ou contínua. Exemplos de variáveis ordinais incluem itens Likert (por exemplo, uma escala de 5 pontos que varia de “discordo totalmente” a “concordo totalmente”). Exemplos de variáveis contínuas incluem altura (medida em polegadas), peso (medido em libras) ou pontuações em testes (medidos de 0 a 100).
- Independência: Todas as observações de ambos os grupos são independentes umas das outras.
- Forma: As formas das distribuições para os dois grupos são aproximadamente as mesmas.
Se essas suposições forem atendidas, você poderá realizar um teste U de Mann-Whitney.
Como realizar um teste U de Mann-Whitney
Para realizar um teste U de Mann-Whitney, seguimos o procedimento padrão de teste de hipótese de cinco etapas :
1. Indique as suposições.
Na maioria dos casos, o teste U de Mann-Whitney é realizado como um teste bicaudal. As hipóteses nula e alternativa são escritas na forma:
H 0 : As duas populações são iguais
H a : As duas populações não são iguais
2. Determine um nível de significância a ser usado para a hipótese.
Decida um nível de significância. As escolhas comuns são 0,01, 0,05 e 0,1.
3. Encontre a estatística de teste.
A estatística de teste é denotada por U e é a menor entre U 1 e U 2 , conforme definido abaixo:
você 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
você 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
onde n 1 e n 2 são os tamanhos das amostras para as amostras 1 e 2, respectivamente, e R 1 e R 2 são a soma das classificações para as amostras 1 e 2, respectivamente.
Os exemplos abaixo mostrarão como encontrar essa estatística de teste em detalhes.
4. Rejeite ou não rejeite a hipótese nula.
Usando as estatísticas de teste, determine se você pode ou não rejeitar a hipótese nula com base no nível de significância e no valor crítico encontrados na tabela U de Mann-Whitney.
5. Interprete os resultados.
Interprete os resultados do teste no contexto da pergunta feita.
Exemplos de realização de um teste U de Mann-Whitney
Os exemplos a seguir mostram como realizar um teste U de Mann-Whitney.
Exemplo 1
Queremos saber se um novo medicamento é eficaz ou não na prevenção de ataques de pânico. Um total de 12 pacientes são divididos aleatoriamente em dois grupos de 6 e designados para receber o novo medicamento ou o placebo. Os pacientes então registram o número de ataques de pânico que sofreram ao longo de um mês.
Os resultados são mostrados abaixo:
| NOVA DROGA | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Realize um teste U de Mann-Whitney para ver se há uma diferença no número de ataques de pânico entre os pacientes do grupo placebo em comparação com o grupo do novo medicamento. Use um nível de significância de 0,05.
1. Indique as suposições.
H 0 : As duas populações são iguais
H a : As duas populações não são iguais
2. Determine um nível de significância a ser usado para a hipótese.
O problema nos diz que devemos usar um nível de significância de 0,05.
3. Encontre a estatística de teste.
Lembre-se de que a estatística de teste é denotada como U e é a menor entre U 1 e U 2 , conforme definido abaixo:
você 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
você 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
onde n 1 e n 2 são os tamanhos das amostras para as amostras 1 e 2, respectivamente, e R 1 e R 2 são a soma das classificações para as amostras 1 e 2, respectivamente.
Para encontrar R 1 e R 2 , precisamos combinar as observações de ambos os grupos e ordená-las do menor para o maior:
| NOVA DROGA | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Amostra total: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
Classificações: 1,5 , 1,5 , 3 , 4,5 , 4,5 , 6,5 , 6,5 , 8,5 , 8,5 , 10 , 11 , 12
R 1 = soma das classificações da amostra 1 = 1,5+4,5+4,5+6,5+8,5+8,5 = 34
R 2 = soma das classificações da amostra 2 = 1,5+3+6,5+10+11+12 = 44
Em seguida, usamos nossos tamanhos de amostra n 1 e n 2 , bem como nossa soma de classificação R 1 e R 2 para encontrar U 1 e U 2 .
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
Nossas estatísticas de teste são as menores entre U1 e U2 , que são U=13.
Nota: Também poderíamos usar a calculadora do teste U de Mann-Whitney para determinar que U = 13.
4. Rejeite ou não rejeite a hipótese nula.
Usando n 1 = 6 e n 2 = 6 com um nível de significância de 0,05, a tabela U de Mann-Whitney nos diz que o valor crítico é 5:
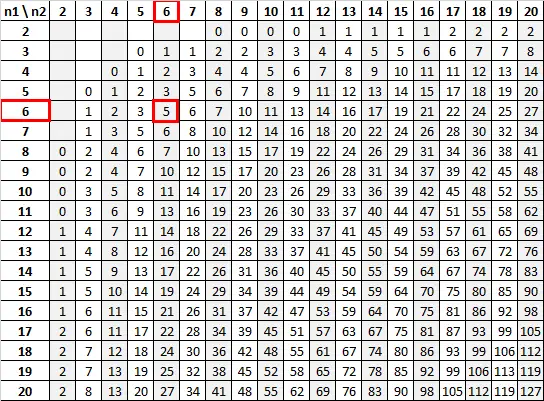
Como nossa estatística de teste (13) é maior que nosso valor crítico (5), não conseguimos rejeitar a hipótese nula.
5. Interprete os resultados.
Como não conseguimos rejeitar a hipótese nula, não temos evidências suficientes para dizer que o número de ataques de pânico sofridos pelos pacientes do grupo placebo seja diferente daquele do grupo do novo medicamento.
Exemplo 2
Queremos saber se estudar 30 minutos por dia durante uma semana ajuda os alunos a terem um melhor desempenho em uma prova. Um total de 15 pacientes são designados aleatoriamente para estudar ou nenhum grupo de estudo. Depois de uma semana, todos os alunos fazem o mesmo teste.
Os resultados dos testes para ambos os grupos são mostrados abaixo:
| ESTUDAR | NENHUM ESTUDO |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Realize um teste U de Mann-Whitney para ver se há uma diferença nas pontuações dos testes para o grupo de estudo em comparação com o grupo sem estudo. Use um nível de significância de 0,01.
1. Indique as suposições.
H 0 : As duas populações são iguais
H a : As duas populações não são iguais
2. Determine um nível de significância a ser usado para a hipótese.
O problema nos diz que devemos usar um nível de significância de 0,01.
3. Encontre a estatística de teste.
Lembre-se de que a estatística de teste é denotada como U e é a menor entre U 1 e U 2 , conforme definido abaixo:
você 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
você 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
onde n 1 e n 2 são os tamanhos das amostras para as amostras 1 e 2, respectivamente, e R 1 e R 2 são a soma das classificações para as amostras 1 e 2, respectivamente.
Para encontrar R 1 e R 2 , precisamos combinar as observações de ambos os grupos e ordená-las do menor para o maior:
| ESTUDAR | NENHUM ESTUDO |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Amostra total: 72 , 75 , 80 , 81, 84, 88 , 89 , 90 , 91 , 92 , 93 , 94 , 95 , 96 , 99
Linhas: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
R 1 = soma das classificações da amostra 1 = 5+7+8+9+10+12+14+15 = 80
R 2 = soma das classificações da amostra 2 = 1+2+3+4+6+11+13 = 40
Em seguida, usamos nossos tamanhos de amostra n 1 e n 2 , bem como nossa soma de classificação R 1 e R 2 para encontrar U 1 e U 2 .
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
Nossas estatísticas de teste são as menores entre U1 e U2 , que são U=12.
Nota: Também poderíamos usar a calculadora do teste U de Mann-Whitney para determinar que U = 12.
4. Rejeite ou não rejeite a hipótese nula.
Usando n 1 = 8 e n 2 = 7 com um nível de significância de 0,01, a tabela U de Mann-Whitney nos diz que o valor crítico é 6:
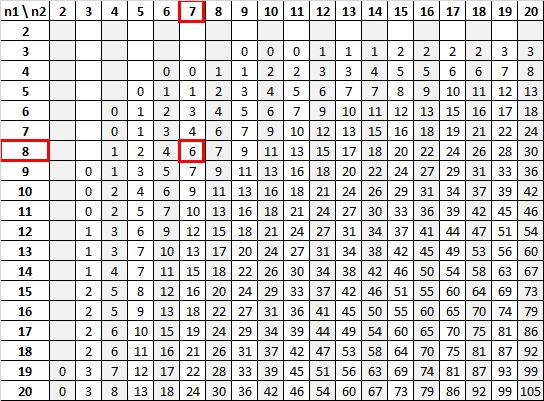
Como nossa estatística de teste (12) é maior que nosso valor crítico (6), não conseguimos rejeitar a hipótese nula.
5. Interprete os resultados.
Como não conseguimos rejeitar a hipótese nula, não temos evidências suficientes para dizer que os resultados dos testes dos alunos que estudaram são diferentes daqueles dos alunos que não estudaram.
Recursos adicionais
Calculadora de teste Mann-Whitney U
Mesa U Mann-Whitney
Como realizar um teste U de Mann-Whitney no Excel
Como realizar um teste U de Mann-Whitney em R
Como realizar um teste U de Mann-Whitney em Python
Como realizar um teste U de Mann-Whitney no SPSS
Como realizar um teste U de Mann-Whitney no Stata
About Author
Dr. benjamim anderson
Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais