Como realizar um teste u de mann-whitney no sas
Um teste U de Mann-Whitney (às vezes chamado de teste de soma de postos de Wilcoxon) é usado para comparar diferenças entre duas amostras quando as distribuições amostrais não são normalmente distribuídas e os tamanhos das amostras são pequenos (n <30).
É considerado o equivalente não paramétrico do teste t para duas amostras .
Este tutorial explica como realizar um teste U de Mann-Whitney no SAS.
Exemplo: teste U de Mann-Whitney no SAS
Suponha que os pesquisadores queiram saber se um tratamento de combustível causa uma alteração no consumo médio de mpg de um carro. Para testar isso, eles realizam um experimento no qual medem o mpg de 12 carros com tratamento de combustível e 12 carros sem tratamento.
Os resultados são mostrados abaixo:
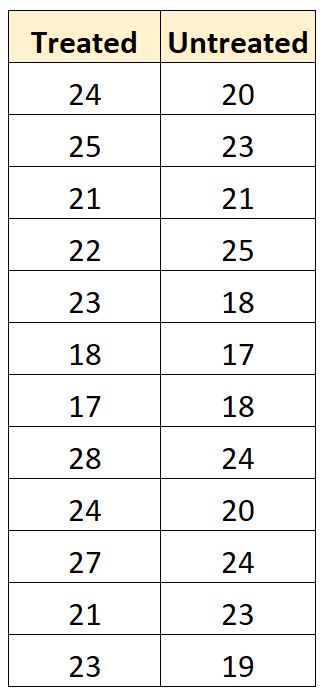
Como os tamanhos amostrais são pequenos e eles suspeitam que as distribuições amostrais não são normalmente distribuídas , eles decidem realizar um teste U de Mann-Whitney para determinar se há uma diferença estatisticamente significativa em mpg entre os dois grupos.
Siga as etapas a seguir para realizar um teste U de Mann-Whitney no SAS.
Etapa 1: crie o conjunto de dados
Primeiro, usaremos o seguinte código para criar o conjunto de dados no SAS:
/*create dataset*/ data mpg_data; input group $mpg; datalines ; treated 24 treated 25 treated 21 treated 22 treated 23 treated 18 treated 17 treated 28 treated 24 treated 27 treated 21 treated 23 untreated 20 untreated 23 untreated 21 untreated 25 untreated 18 untreated 17 untreated 18 untreated 24 untreated 20 untreated 24 untreated 23 untreated 19 ; run ;
Etapa 2: realizar o teste U de Mann Whitney
A seguir, usaremos proc npar1way para realizar o teste U de Mann Whitney:
/*perform Mann Whitney U test*/
proc npar1way data =mpg_data wilcoxon ;
classgroup ;
var mpg;
run;
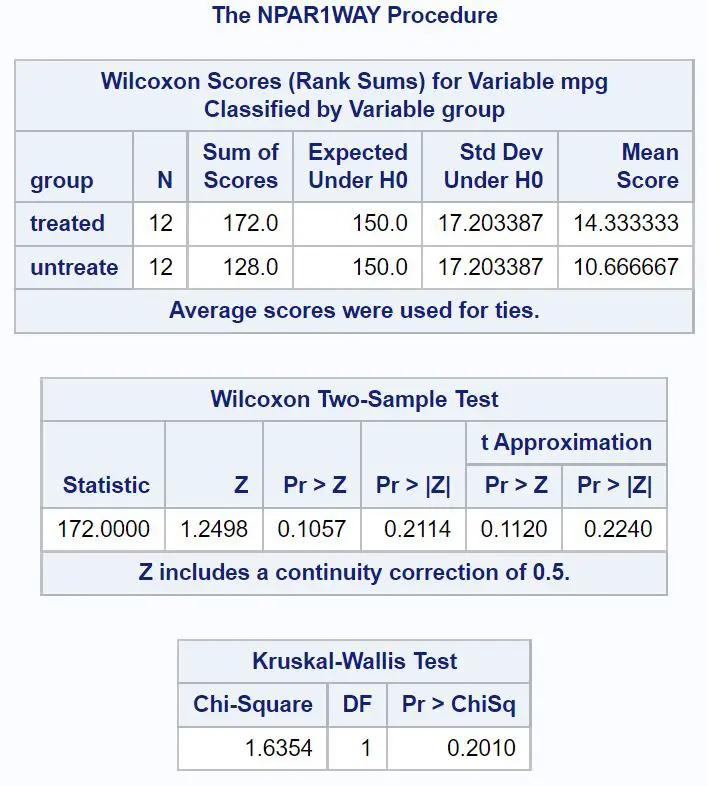
Na tabela de teste de duas amostras de Wilcoxon, vemos que o valor p bicaudal do teste acaba sendo 0,2114 .
Lembre-se que o teste U de Mann Whitney utiliza as seguintes hipóteses nulas e alternativas:
- H 0 : As duas populações têm a mesma mediana.
- HA : As duas populações têm medianas diferentes.
Como o valor p do teste ( 0,2114 ) não é inferior a 0,05, não rejeitamos a hipótese nula.
Isso significa que não temos evidências suficientes para dizer que o mpg é diferente entre carros que recebem tratamento de combustível e aqueles que não recebem.
O SAS também fornece boxplots para visualizar a distribuição dos valores de mpg para cada grupo:
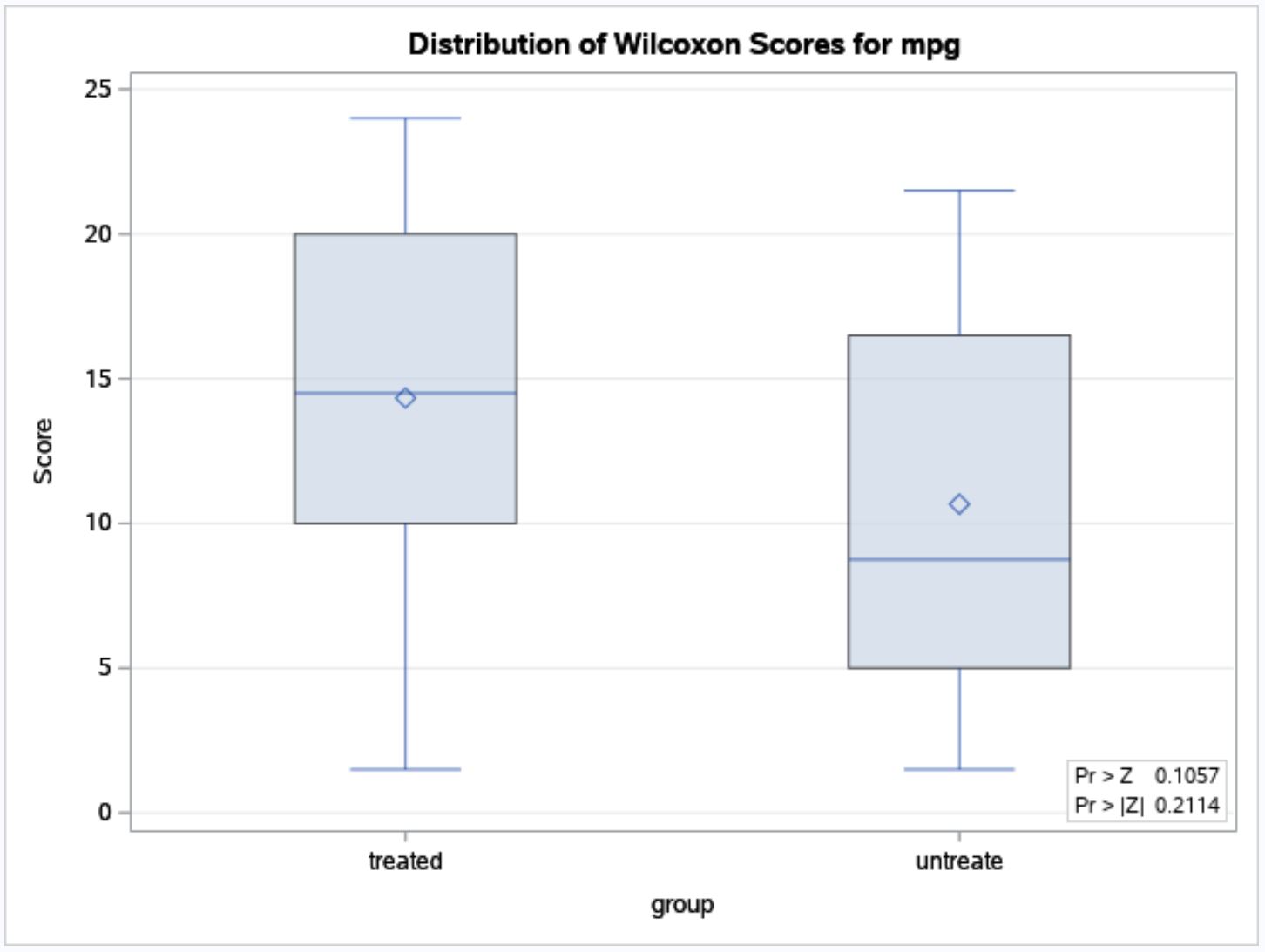
No gráfico podemos ver que os carros que receberam o tratamento de combustível tenderam a ter valores de mpg mais elevados, mas a partir dos resultados do teste Mann Whitney U sabemos que as diferenças entre os dois grupos não foram estatisticamente significativas.
Recursos adicionais
Os tutoriais a seguir explicam como realizar outros testes estatísticos comuns no SAS:
Como realizar um teste t de uma amostra no SAS
Como realizar um teste t de duas amostras no SAS
Como realizar um teste t de amostras pareadas no SAS
Como realizar um teste de classificação assinada de Wilcoxon no SAS