Como criar uma matriz de covariância em python

A covariância é uma medida de como as mudanças em uma variável estão associadas às mudanças em uma segunda variável. Mais especificamente, é uma medida do grau em que duas variáveis estão linearmente associadas.

Uma matriz de covariância é uma matriz quadrada que mostra a covariância entre muitas variáveis diferentes. Esta pode ser uma forma útil de compreender como diferentes variáveis estão relacionadas em um conjunto de dados.

O exemplo a seguir mostra como criar uma matriz de covariância em Python.

Como criar uma matriz de covariância em Python

Use as etapas a seguir para criar uma matriz de covariância em Python.

Etapa 1: crie o conjunto de dados.

Primeiro, criaremos um conjunto de dados contendo as notas de testes de 10 alunos diferentes em três disciplinas: matemática, ciências e história.

 import numpy as np

math = [84, 82, 81, 89, 73, 94, 92, 70, 88, 95]
science = [85, 82, 72, 77, 75, 89, 95, 84, 77, 94]
history = [97, 94, 93, 95, 88, 82, 78, 84, 69, 78]

data = np.array([math, science, history])

Etapa 2: Crie a matriz de covariância.

A seguir, criaremos a matriz de covariância para este conjunto de dados usando a função numpy cov() , especificando que bias = True para que possamos calcular a matriz de covariância populacional.

 np.cov(data, bias= True )

array([[ 64.96, 33.2, -24.44],
       [33.2, 56.4, -24.1],
       [-24.44, -24.1, 75.56]])

Etapa 3: interprete a matriz de covariância.

Os valores ao longo das diagonais da matriz são simplesmente as variâncias de cada assunto. Por exemplo:

• A variância das pontuações em matemática é 64,96
• A variação das pontuações em ciências é 56,4
• A variação histórica da pontuação é 75,56

Os demais valores da matriz representam as covariâncias entre os diferentes assuntos. Por exemplo:

• A covariância entre as pontuações em matemática e ciências é 33,2.
• A covariância entre as pontuações em matemática e história é -24,44.
• A covariância entre as pontuações de ciência e história é -24,1.

Um número positivo para covariância indica que duas variáveis tendem a aumentar ou diminuir em conjunto. Por exemplo, matemática e ciências têm uma covariância positiva (33,2), indicando que os alunos com notas altas em matemática também tendem a ter notas altas em ciências. Por outro lado, os alunos com mau desempenho em matemática também tendem a ter mau desempenho em ciências.

Um número negativo para covariância indica que à medida que uma variável aumenta, uma segunda variável tende a diminuir. Por exemplo, matemática e história têm uma covariância negativa (-24,44), indicando que os alunos com notas altas em matemática tendem a ter notas baixas em história. Por outro lado, os alunos com notas baixas em matemática tendem a ter notas altas em história.

Passo 4: Visualize a matriz de covariância (opcional).

Você pode visualizar a matriz de covariância usando a função heatmap() do pacote seaborn:

 import seaborn as sns
import matplotlib.pyplot as plt

cov = np.cov(data, bias=True)
labs = ['math', 'science', 'history']

sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs)
plt.show()

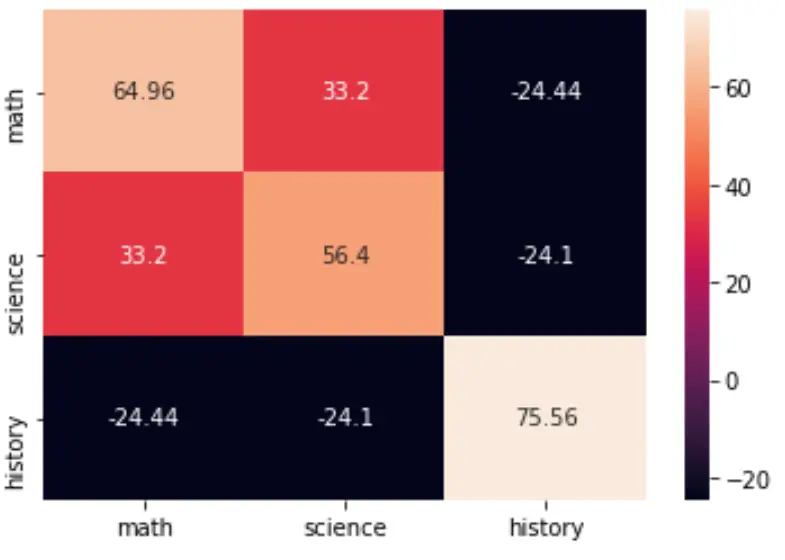
Você também pode alterar a paleta de cores especificando o argumento cmap :

 sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs, cmap=' YlGnBu ')
plt.show() 

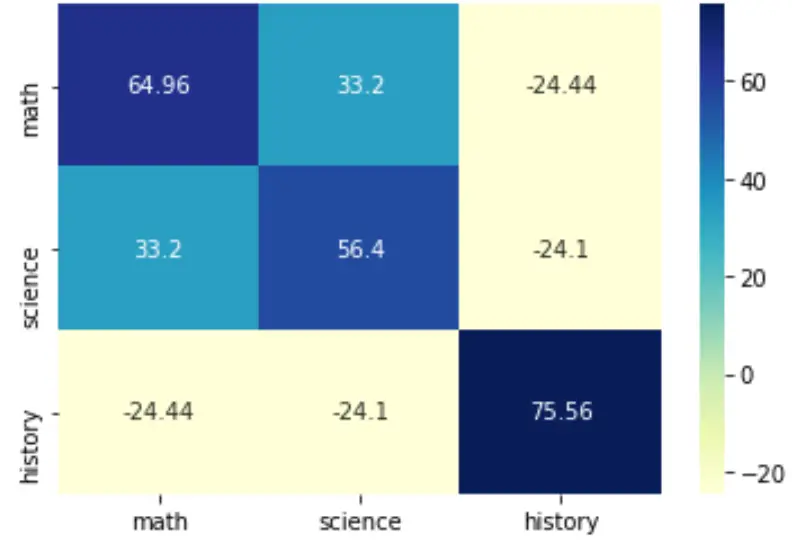
Para obter mais detalhes sobre como estilizar este mapa de calor, consulte a documentação do Seaborn .