Como criar uma matriz de covariância no spss
A covariância é uma medida de como as mudanças em uma variável estão associadas às mudanças em uma segunda variável. Mais especificamente, é uma medida do grau em que duas variáveis estão linearmente associadas.
A fórmula para calcular a covariância entre duas variáveis, X e Y é:
COV( X , Y ) = Σ(x- x )(y- y ) / n
Uma matriz de covariância é uma matriz quadrada que mostra a covariância entre diferentes variáveis em um conjunto de dados.
Este tutorial explica como criar uma matriz de covariância para um determinado conjunto de dados no SPSS.
Exemplo: Matriz de covariância em SPSS
Suponha que temos o seguinte conjunto de dados que mostra as pontuações dos testes de 10 alunos diferentes em três disciplinas: matemática, ciências e história:
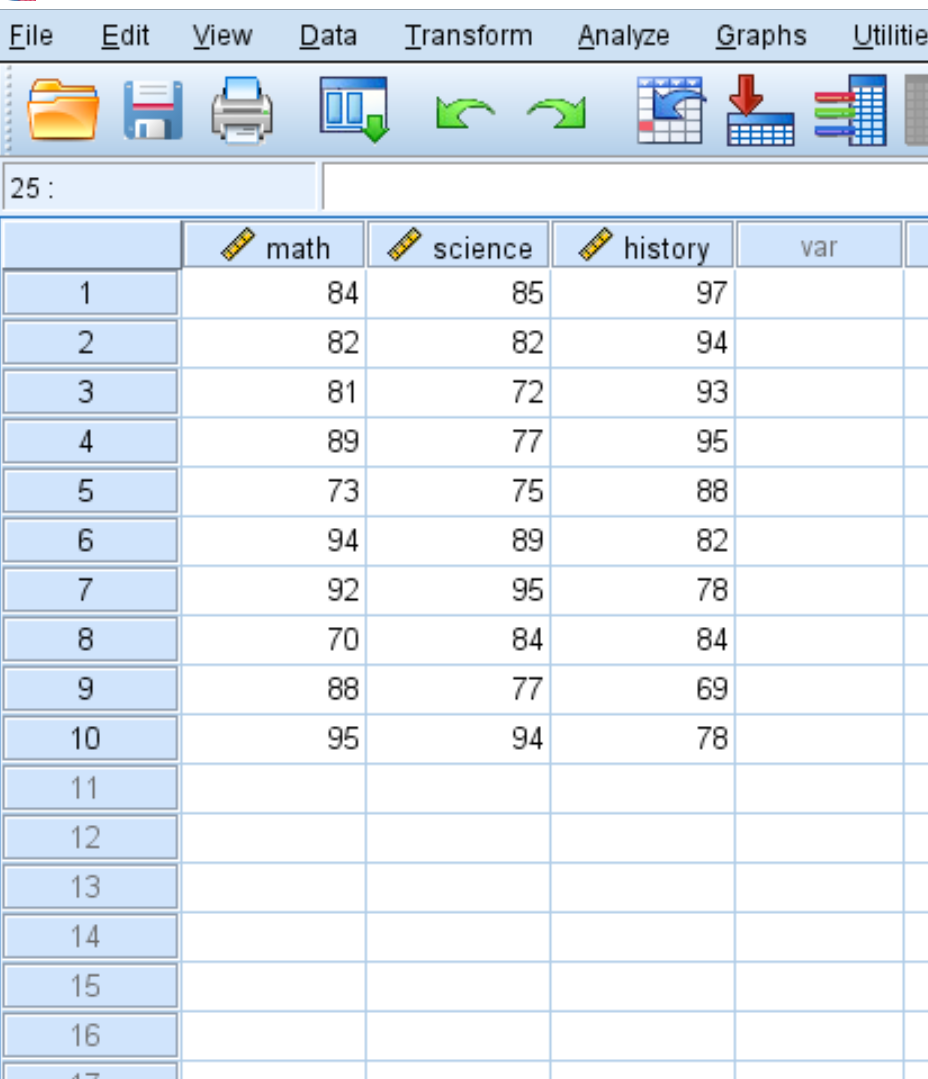
Para criar uma matriz de covariância para este conjunto de dados, clique na guia Analisar , em Correlacionar e em Bivariado :
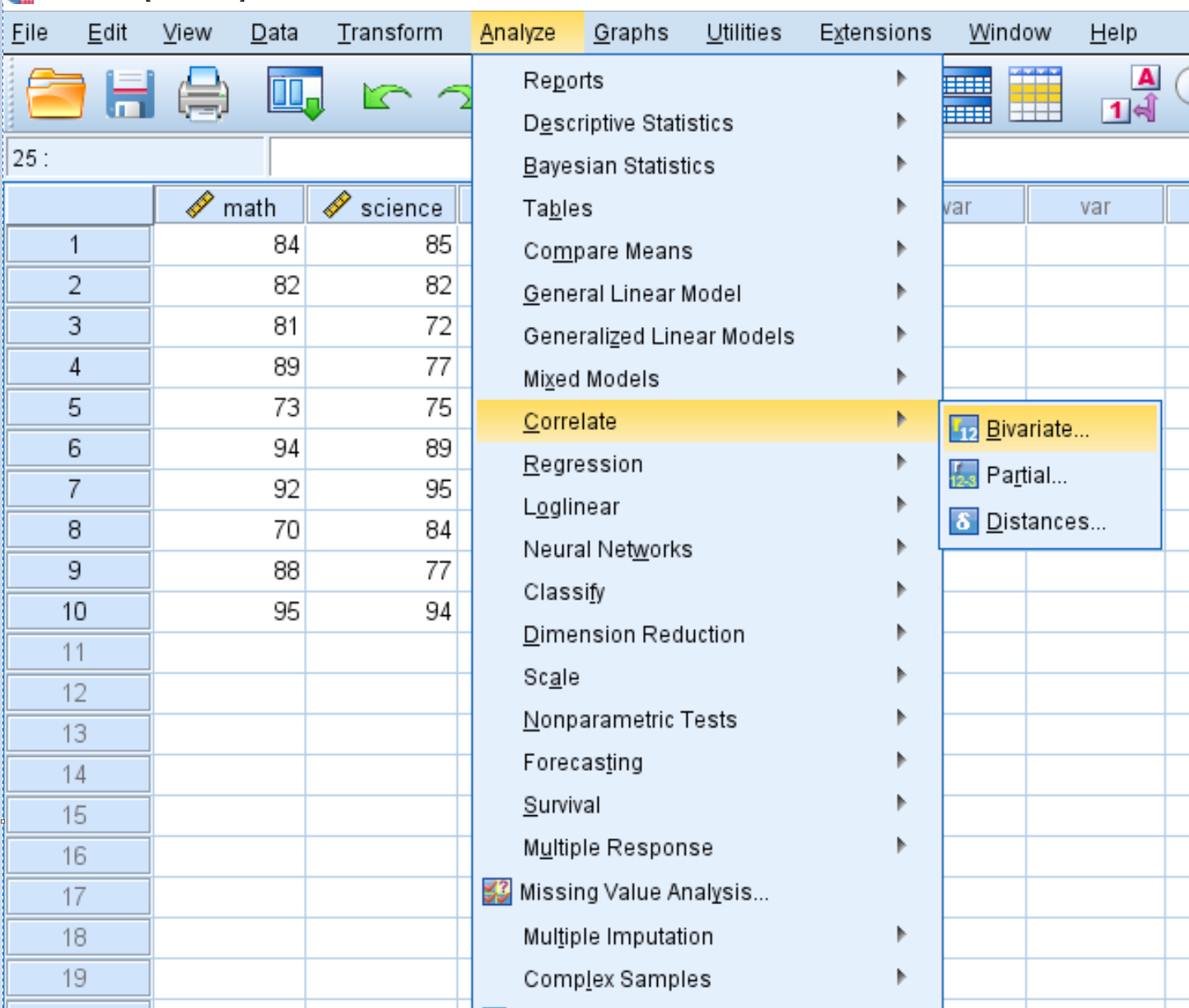
Na nova janela que aparece, arraste cada uma das três variáveis para a caixa denominada Variáveis :

Em seguida, clique em Opções . Marque a caixa ao lado de Variações e covariâncias entre produtos . Em seguida, clique em Continuar .
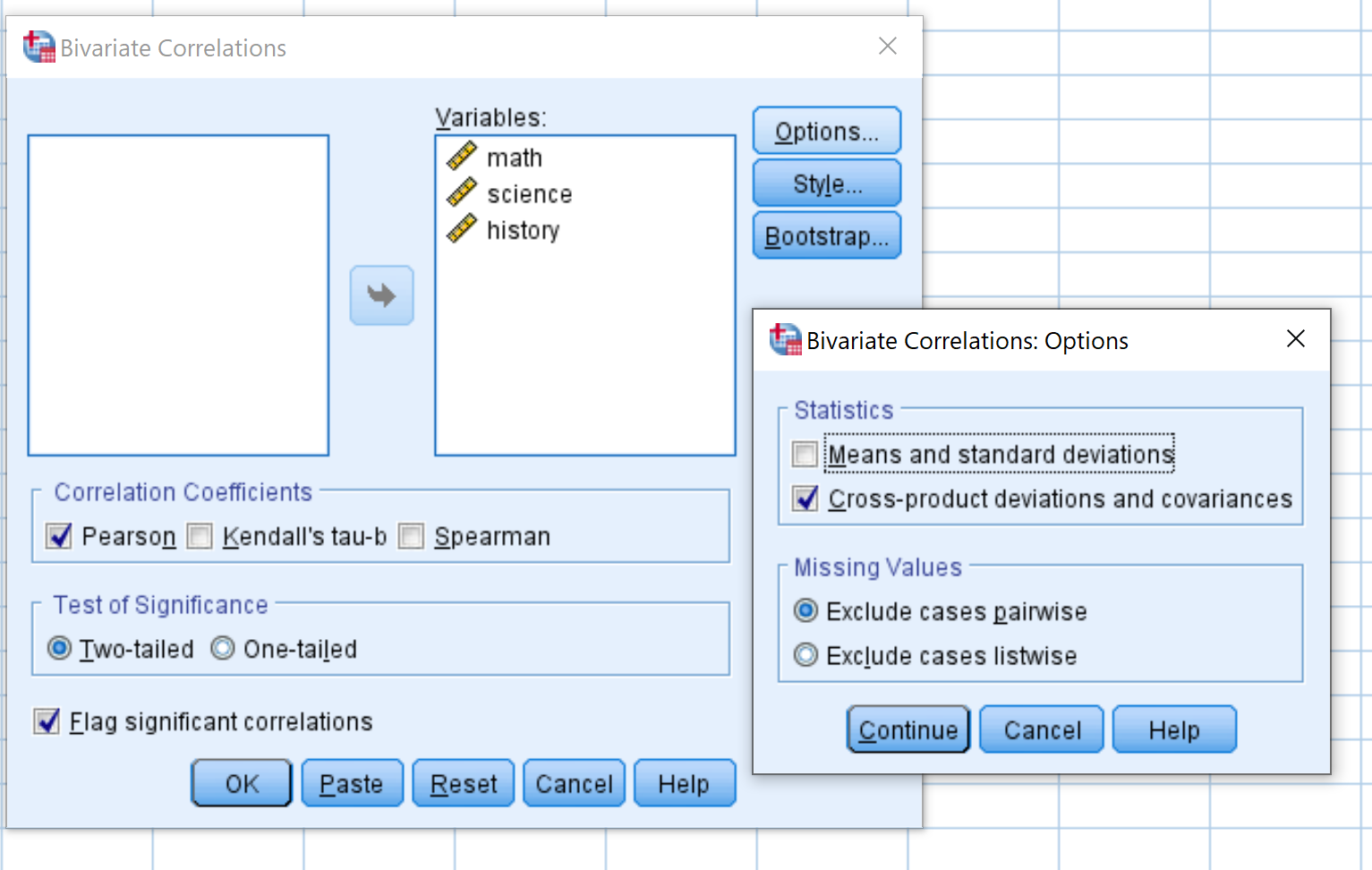
Em seguida, clique em OK . O resultado aparecerá em uma nova janela:
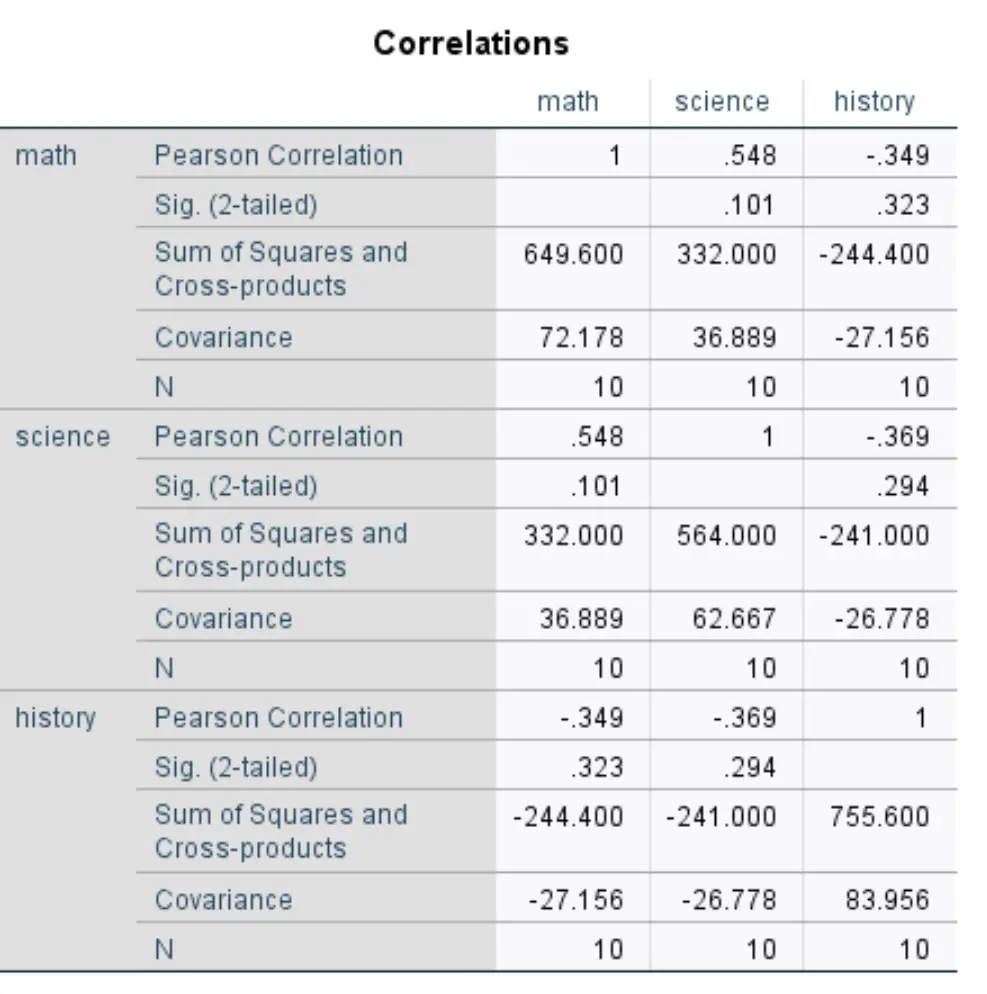
Para obter a covariância para cada combinação de variáveis em pares, você precisa dividir a soma dos quadrados e dos produtos vetoriais por N.
Por exemplo, a covariância entre matemática e ciências pode ser calculada da seguinte forma:
COV (matemática, ciências) = 332.000 / 10 = 33,2 .
Da mesma forma, a covariância entre matemática e história pode ser calculada da seguinte forma:
COV (matemática, história) = -244,400 / 10 = -24,44 .
Você também pode obter a variância de cada variável dividindo a soma dos quadrados e dos produtos vetoriais por N.
Por exemplo, a variância em matemática pode ser calculada da seguinte forma:
VAR(matemática) = 649,600 / 10 = 64,96 .
Você pode obter a matriz de covariância completa para este conjunto de dados realizando cálculos semelhantes:
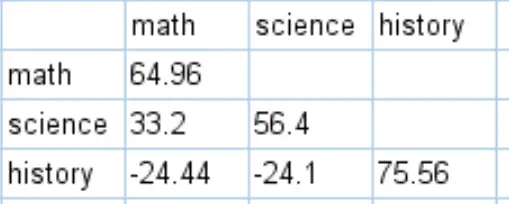
Como interpretar uma matriz de covariância
Os valores ao longo das diagonais da matriz de covariâncias são simplesmente as variâncias de cada sujeito. Por exemplo:
- A variância dos resultados matemáticos é 64,96 .
- A variância das pontuações em ciências é 56,4 .
- A variância das pontuações históricas é 75,56 .
Os demais valores da matriz representam as covariâncias entre os diferentes assuntos. Por exemplo:
- A covariância entre as pontuações em matemática e ciências é 33,2 .
- A covariância entre as pontuações em matemática e história é -24,44 .
- A covariância entre as pontuações de ciência e história é -24,1 .
Um número positivo para covariância indica que duas variáveis tendem a aumentar ou diminuir em conjunto. Por exemplo, matemática e ciências têm uma covariância positiva (33,2), indicando que os alunos com notas altas em matemática também tendem a ter notas altas em ciências. Da mesma forma, os alunos com mau desempenho em matemática também tendem a ter mau desempenho em ciências.
Um número negativo para covariância indica que à medida que uma variável aumenta, uma segunda variável tende a diminuir. Por exemplo, ciências e história têm uma covariância negativa (-24,1), indicando que os alunos com notas altas em ciências tendem a ter notas baixas em história. Da mesma forma, os alunos com notas baixas em ciências tendem a ter notas altas em história.
Recursos adicionais
Como criar uma matriz de correlação no SPSS
Como calcular a correlação parcial no SPSS