Matriz de covariância

Este artigo explica o que é a matriz de covariância e qual é sua fórmula. Você descobrirá como criar a matriz de covariância com um exemplo concreto e as propriedades das matrizes de covariância.

Qual é a matriz de covariância?

A matriz de covariâncias é uma matriz quadrada cujos elementos são as variâncias e covariâncias das variáveis estudadas. Assim, os elementos da diagonal principal da matriz de covariâncias são as variâncias de cada variável, e os demais elementos são as covariâncias entre as variáveis.

Nas estatísticas, a matriz de covariância é utilizada para analisar a relação entre duas ou mais variáveis aleatórias. A matriz de covariâncias é muito útil porque permite interpretar rapidamente a correlação entre muitas variáveis, já que é possível ver os valores de todas as covariâncias das variáveis ao mesmo tempo.

O símbolo da matriz de covariância é a letra grega maiúscula sigma (Σ).

Como calcular a matriz de covariância

Para calcular a matriz de covariância de diversas variáveis estatísticas, devem ser realizados os seguintes passos:

1. Calcule as variâncias de todas as variáveis.
2. Calcule a covariância de cada par de variáveis.
3. Forme a matriz de covariância:
• A variância da variável i deve ser colocada na diagonal principal da matriz, mais precisamente na posição i,i .
• A covariância entre as variáveis i e j deve ser colocada na posição i,j da matriz.

A fórmula para a matriz de covariância é, portanto, a seguinte:

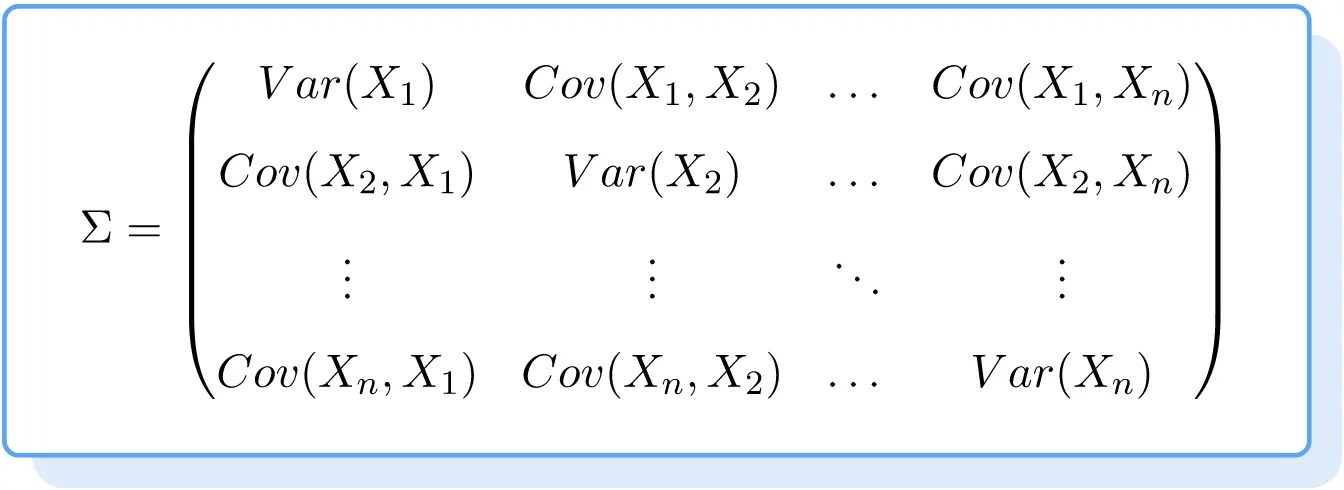
Exemplo de matriz de covariância

Depois de ver a definição de matriz de covariância, segue abaixo um passo a passo para você ver como é feito esse tipo de matriz.

Calcula a matriz de covariâncias das variáveis X, Y e Z, cujos valores são:

• X: 4, 7, 12, 5, 7
• E: 9, 15, 19, 6, 8
• Z: 7, 2, 4, 6, 3

A primeira coisa que precisamos fazer é determinar as variâncias de todas as variáveis:

Em segundo lugar, encontramos a covariância entre cada par de variáveis:

E uma vez calculadas todas as variâncias e covariâncias, só falta fazer a matriz de covariâncias. Para fazer isso, colocamos os valores de variância na diagonal principal da matriz e os valores de covariância em suas posições correspondentes:

Como você pode ver, ao representar as variâncias e covariâncias em uma matriz, é muito fácil interpretar as variáveis. A variável com maior dispersão é Y (23,44), por outro lado as variáveis X e Y possuem relação direta, enquanto as variáveis X e Z (e portanto Y e Z) possuem relação inversa.

Observe que a matriz de covariância é sempre simétrica, pois a covariância entre duas variáveis não depende da ordem das variáveis. Por exemplo,

é igual a

Além disso, a matriz de covariância será sempre uma matriz quadrada e sua dimensão será igual ao número de variáveis. Neste caso tínhamos três variáveis e por isso é uma matriz 3×3, mas se tivéssemos apenas duas variáveis a matriz de covariância teria sido 2×2.

Propriedades da matriz de covariância

A matriz de covariância possui as seguintes características:

• A matriz de covariância é uma matriz quadrada da ordem do número de variáveis.
• A matriz de covariância é simétrica, o que significa que a diagonal principal da matriz é um eixo de simetria.
• A matriz de covariância é sempre positiva semidefinida.
• O determinante da matriz de covariância é igual ou maior que zero.