Média amostral

Neste artigo você descobrirá qual é a média amostral nas estatísticas. Da mesma forma, você encontrará como calcular a média de uma amostra, um exercício resolvido e, além disso, uma calculadora online para calcular a média de qualquer amostra.

Qual é a média da amostra?

Nas estatísticas, a média amostral é a média dos valores de uma amostra. Para calcular a média amostral, todos os valores da amostra devem ser somados e depois divididos pelo número total de dados da amostra.

O símbolo para as médias amostrais é

.

Num estudo estatístico, geralmente nem todos os valores de uma população são conhecidos, por isso se seleciona uma amostra da população para analisá-la e extrapolar as conclusões obtidas para toda a população. Assim, a média amostral é usada para estimar a média populacional.

Exemplo de fórmula média

A média amostral é igual à soma de todos os valores amostrais dividida pelo tamanho da amostra. Ou seja, para calcular a média amostral, todos os valores da amostra são somados e depois divididos pelo número total de dados da amostra.

Portanto, a fórmula para cálculo da média amostral é:

👉 Você pode usar a calculadora abaixo para calcular a média amostral de qualquer conjunto de dados.

Tenha em mente que a média amostral é calculada usando dados de uma amostra, portanto o valor da média populacional pode diferir do valor calculado.

Exemplo de cálculo de média amostral

Agora que sabemos a definição de média amostral e qual é sua fórmula, vamos ver como obter a média amostral de um conjunto de dados resolvendo um exemplo simples.

• José quer mudar-se para o centro da cidade, mas não tem muito tempo e não consegue analisar os preços de todos os apartamentos para alugar. Então você decide olhar apenas o preço do aluguel de cinco apartamentos (mostrados abaixo) para saber quanto custará morar no centro da cidade. Qual é o preço médio da amostra?

600 € 430 € 820 € 575 € 950

Para encontrar a média amostral, precisamos somar todos os valores amostrais e depois dividir pelo número total de observações, que é 5. Então, aplicamos a fórmula da média amostral:

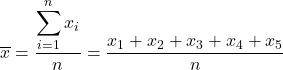
A seguir, substituímos os dados na fórmula e calculamos a média amostral:

Em suma, o preço médio da amostra de apartamentos selecionados para a amostra é de 675€.

Exemplo de calculadora média

Insira dados de qualquer amostra estatística na calculadora a seguir para calcular sua média amostral. Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.

Média amostral e média populacional

A média da população é a média da população estatística . A média populacional é, portanto, a média de todos os elementos sobre os quais se pretende realizar um estudo estatístico.

Portanto, a diferença entre a média amostral e a média populacional é que a média amostral é a média dos valores amostrais, enquanto a média populacional é a média dos valores da população.

Para diferenciar a média amostral da média populacional, elas são representadas por símbolos diferentes. O símbolo para as médias amostrais é

, enquanto o símbolo para a população significa é

.

A média amostral é usada para estimar o valor da média populacional, o que pode ser feito usando estimativa pontual ou estimativa intervalar .

Distribuição amostral das médias amostrais

Por fim, vejamos o que significa a distribuição amostral da amostra, pois é um conceito estatístico que pode ser confuso.

Primeiro, vamos começar definindo o que é uma distribuição amostral. Uma distribuição amostral é a distribuição que resulta da consideração de todas as amostras possíveis de uma população estatística.

Portanto, a distribuição amostral da média amostral é a distribuição que resulta do cálculo da média de cada amostra possível de uma população. Ou seja, se estudarmos todas as amostras possíveis de uma população e calcularmos a média de cada uma das amostras, o conjunto de valores calculados é uma distribuição amostral da média amostral.

Concluindo, embora a média amostral e a distribuição amostral tenham nomes semelhantes, é necessário saber distingui-las: a média amostral é um parâmetro estatístico que é calculado a partir de uma amostra, por outro lado, uma distribuição amostral é uma distribuição que resulta do estudo de todas as amostras que podem ser feitas a partir de uma população.