Média aritmética

By Dr. benjamim anderson Agosto 6, 2023 Estatisticas 0 Comments

Aqui explicamos o que é a média aritmética e como ela é calculada. Você encontrará exemplos de média aritmética e até mesmo uma calculadora para encontrar a média aritmética de qualquer amostra estatística. Por fim, você poderá ver quais são as propriedades desse tipo de média e como a média aritmética é obtida com dados agrupados em intervalos.

Qual é a média aritmética?

A média aritmética é um valor central característico de um conjunto de dados estatísticos. Para calcular a média aritmética, todos os valores são somados e divididos pelo número total de dados.

Além disso, a média aritmética é um dos principais indicadores utilizados para realizar um estudo estatístico de uma amostra.

A fórmula para a média aritmética é, portanto, a seguinte:

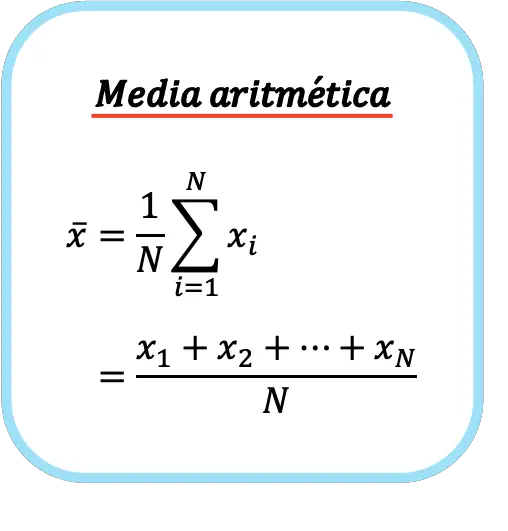
O símbolo da média aritmética é uma faixa horizontal acima da letra x.

$(\overline{x}).$

Você também pode diferenciar a média amostral da média populacional com o símbolo de média: a média de uma amostra é expressa com o símbolo

$\overline{x}$

, por outro lado, para a média de uma população, usamos a letra grega

$\mu.$

Ressalta-se que a média aritmética de uma população equivale ao valor esperado da variável estatística.

A média aritmética, também chamada de média aritmética, não é o único tipo de média que existe, existe também a média ponderada, a média quadrada, a média geométrica e a média harmônica, entre outras. Você pode ver como cada um deles é calculado no mecanismo de busca do nosso site.

Como calcular a média aritmética

Para calcular a média aritmética, as seguintes etapas devem ser executadas:

Adicione todos os dados estatísticos da amostra.
Divida a soma anterior pelo número total de dados.
O resultado obtido é a média aritmética da amostra estatística.

👉 Você pode usar a calculadora abaixo para calcular a média aritmética de qualquer conjunto de dados.

Exemplo de cálculo da média aritmética

Dada a definição de média aritmética, veremos como obter a média aritmética de um conjunto de dados resolvendo um exemplo passo a passo.

Um aluno obteve as seguintes notas durante um ano letivo: em matemática 9, em línguas 7, em história 6, em economia 8 e em ciências 7,5. Qual é a média aritmética de todas as suas notas?

Para encontrar a média aritmética, precisamos somar todas as notas e depois dividir pelo total de disciplinas do curso, que é 5. Portanto, aplicamos a fórmula da média aritmética:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+x_3+x_4+x_5}{N}$

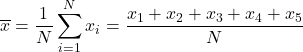
Substituímos os dados na fórmula e calculamos a média aritmética:

$\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3$

Como você pode ver, na média aritmética é atribuído o mesmo peso a cada valor, ou seja, cada dado tem o mesmo peso dentro do todo.

Calculadora de média aritmética

Insira dados de qualquer amostra estatística na calculadora a seguir para calcular sua média aritmética. Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.

Média aritmética para dados agrupados

Por dados agrupados, queremos dizer que os dados são estruturados como grupos ou intervalos. Isso geralmente acontece quando o tamanho da amostra estatística é muito grande.

Portanto o cálculo da média aritmética varia um pouco quando os dados são agrupados, embora o conceito seja o mesmo.

Para calcular a média aritmética dos dados agrupados em intervalos, a pontuação da turma de cada grupo deve ser multiplicada pela sua frequência absoluta e depois dividida pela soma de todas as frequências absolutas.

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{x_1\cdot f_1+ x_2\cdot f_2+\dots +x_N\cdot f_N}{N}$

Nota: A pontuação da classe de um intervalo é calculada dividindo a soma dos pontos finais do intervalo por dois. Por exemplo, a nota de aula do intervalo [3,7) seria:

$\cfrac{3+7}{2}=5$

Para que você possa ver como isso é feito, segue abaixo um exercício resolvido sobre a média aritmética de dados agrupados em intervalos:

Queremos estudar estatisticamente o peso de um grupo, para isso entrevistamos um grupo representativo de 81 pessoas e obtivemos os seguintes dados:

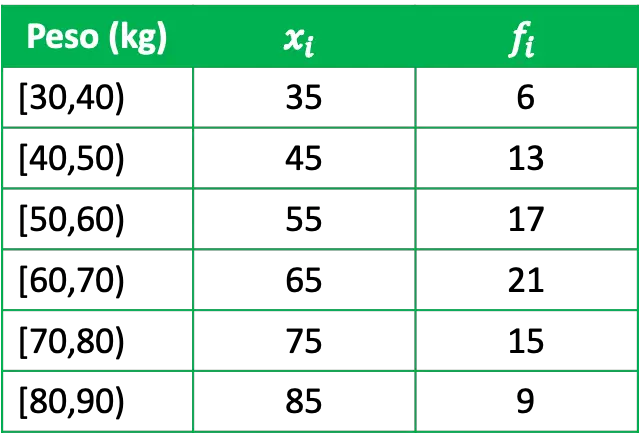
Onde x _i é a nota da turma de cada grupo e f _i sua frequência absoluta, ou seja, a quantidade de pessoas que têm peso nesse intervalo.

Para determinar a média aritmética é necessário adicionar uma coluna na tabela de frequências que é o produto das notas da aula pelas suas respectivas frequências absolutas:

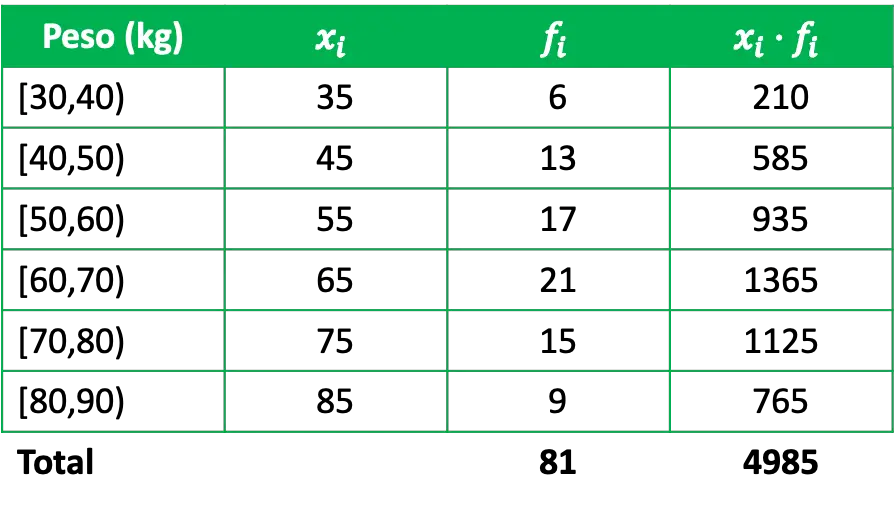
exercício de média aritmética resolvido para dados agrupados

Assim, para calcular a média aritmética dos dados agrupados, basta dividir a soma dos produtos das notas das aulas pelas suas frequências pelo número total de dados:

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{4985}{81}=61,54 \text{ kg}$

Propriedades da média aritmética

A média aritmética possui as seguintes características:

A soma dos desvios de todos os dados em uma distribuição da média resulta em zero.

$\sum_{i=1}^N\left(x_i-\overline{x}\right)=0$

Se adicionarmos a mesma quantidade a todos os dados de uma amostra, a média da amostra aumenta nessa quantidade.

O mesmo acontece com a multiplicação: se multiplicarmos todos os valores de uma amostra por um número, a média amostral é multiplicada por esse número.

A média aritmética só pode ser calculada em variáveis quantitativas . Em outras palavras, você não pode tirar a média das variáveis qualitativas.

A média aritmética será sempre um valor entre o mínimo e o máximo de uma distribuição.

$\text{min}\{x_1,x_2,...,x_N\}\leq \cfrac{x_1+\dots +x_N}{N}\leq \text{max}\{x_1,x_2,...,x_N\}$

Este tipo de média é muito sensível a valores muito altos ou muito baixos, fazendo com que um outlier altere significativamente o resultado da média aritmética.

A média aritmética de um conjunto de dados é sempre igual ou maior que a média geométrica do mesmo conjunto de dados.

$\displaystyle\frac{x_1+x_2+\dots+x_N}{N}\geq \sqrt[N]{x_1+x_2+\dots+x_N}$

Calcule a média aritmética com Excel

Calcular a média aritmética no Excel é muito simples, bastando inserir os dados em uma planilha e utilizar a função MÉDIA .

Por exemplo, para determinar a média aritmética dos dados do primeiro exercício resolvido que explicamos, basta copiar todos os dados em um documento Excel e escrever a seguinte fórmula em uma célula: =MÉDIA(9;7;5; 8;7 ,5) . A função retornará a média aritmética dos dados, que é 7,3.

Obviamente, é muito mais rápido encontrar a média aritmética de certos números com o programa Excel do que calculá-la manualmente, principalmente quando o tamanho da amostra é muito grande.

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais