Desvio médio absoluto versus desvio padrão: qual a diferença?
O desvio padrão é uma das formas mais comuns de medir a dispersão de um conjunto de dados.
É calculado da seguinte forma:
Desvio padrão = √( Σ(x i – x ) 2 / n )
Outra forma de medir a distribuição das observações em um conjunto de dados é o desvio médio absoluto .
É calculado da seguinte forma:
Desvio médio absoluto = Σ|x i – x | /não
Este tutorial explica as diferenças entre essas duas métricas junto com exemplos de como calcular cada uma.
Semelhanças e diferenças
Como o nome sugere, o desvio padrão e o desvio médio absoluto tentam quantificar o desvio típico das observações da média em um determinado conjunto de dados.
No entanto, o método usado por cada métrica é diferente.
Desvio padrão
O desvio padrão encontra a diferença quadrada entre cada observação e a média de um conjunto de dados. Em seguida, calcula a média dessas diferenças quadradas e obtém a raiz quadrada.
Isso nos deixa com um número que representa o desvio “padrão” ou típico de uma observação em relação à média.
Significa desvio absoluto
Por outro lado, o desvio médio absoluto encontra o desvio absoluto entre cada observação e a média do conjunto de dados. Em seguida, encontra a média desses desvios.
Isso nos deixa com um número que representa o desvio médio das observações em relação à média.
Como o desvio padrão encontra diferenças quadradas, será sempre igual ou maior que o desvio médio absoluto.
Quando estão presentes valores discrepantes extremos, o desvio padrão será consideravelmente maior do que o desvio médio absoluto. O exemplo a seguir ilustra esse ponto.
Exemplo: desvio médio absoluto do desvio padrão
Suponha que temos o seguinte conjunto de dados de 8 valores:
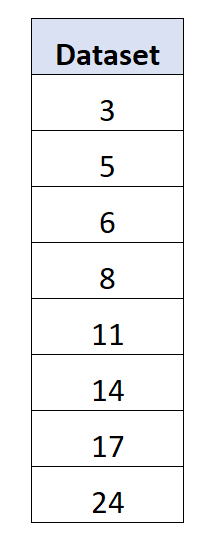
A média acaba sendo 11 .
Portanto, calcularíamos o desvio absoluto médio da seguinte forma:
Desvio médio absoluto = (|3-11| + |5-11| + |6-11| + |8-11| + |11-11| + |14-11| + |17-11| + |24- 11|) / 8 = 5,5 .
E calcularíamos o desvio padrão da seguinte forma:
Desvio padrão = √((3-11) 2 + (5-11) 2 + (6-11) 2 + (8-11) 2 + (11-11) 2 + (14-11) 2 + (17- 11) 2 + (24-11) 2 )/8) = 6,595 .
Conforme mencionado anteriormente, o desvio padrão será sempre igual ou superior ao desvio médio absoluto.
No entanto, a diferença entre o desvio padrão e o desvio médio absoluto será particularmente grande se existirem valores discrepantes extremos no conjunto de dados.
Por exemplo, considere o seguinte conjunto de dados com um valor atípico extremo para o último valor:
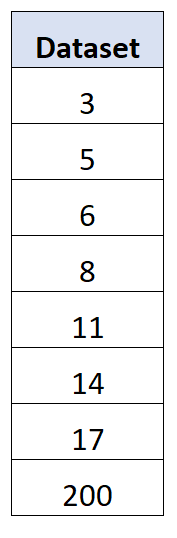
Acontece que o desvio padrão para este conjunto de dados é 63,27 , enquanto o desvio absoluto médio é 41,75 .
O valor discrepante extremo faz com que o desvio padrão seja muito maior do que o desvio absoluto médio.