Meios geométricos

By Dr. benjamim anderson Agosto 6, 2023 Estatisticas 0 Comments

Neste artigo explicamos o que é média geométrica, como ela é calculada e qual a diferença entre média geométrica e média aritmética. Você também poderá ver um exercício resolvido passo a passo da média geométrica e quais são as propriedades desse tipo de média. Finalmente, você encontrará uma calculadora para calcular a média geométrica de qualquer conjunto de dados.

Qual é a média geométrica?

A média geométrica é uma medida da centralidade da estatística descritiva. A média geométrica de um conjunto de dados estatísticos é igual à enésima raiz do produto de todos os valores.

A média geométrica é usada em finanças empresariais para calcular taxas de retorno, médias percentuais e juros compostos.

A fórmula para a média geométrica é, portanto, a seguinte:

A média geométrica só pode ser calculada quando todos os dados da amostra são positivos. Porque se um valor fosse negativo, a raiz teria solução negativa ou nenhuma solução, por outro lado, se um dado fosse zero então a multiplicação dos dados daria zero e, portanto, a média geométrica seria igual a 0.

A média geométrica não é o único tipo de média que existe, existe também a média aritmética, a média ponderada, a média quadrada e a média harmônica.

Diferença entre média geométrica e média aritmética

A principal diferença entre a média geométrica e a média aritmética é que a média geométrica é menos sensível a valores extremos do que a média aritmética. Além disso, a média aritmética pode ser calculada com valores negativos e zero, enquanto a média geométrica só pode ser calculada com valores positivos.

Da mesma forma, a média geométrica será geralmente inferior à média aritmética para o mesmo conjunto de dados.

De referir ainda que o cálculo da média geométrica é mais complexo e por isso a sua significância estatística é mais difícil de interpretar.

Em suma, a média geométrica apresenta vantagens e desvantagens em relação à média aritmética e, dependendo da natureza dos dados, será adequado calcular esta ou aquela média.

Como calcular a média geométrica

Para calcular a média geométrica, devem ser executados os seguintes passos:

Calcule o produto de todos os dados estatísticos da amostra.
Encontre a enésima raiz do produto calculado.
O resultado obtido é a média geométrica da amostra estatística.

Como você pode ver, encontrar a média geométrica de um conjunto de dados é relativamente simples com uma calculadora ou programa de computador, pois basta calcular um produto e uma raiz. Pelo contrário, é bastante trabalhoso fazer o cálculo manualmente.

👉 É por isso que recomendamos usar a calculadora abaixo para calcular a média geométrica de um conjunto de dados.

Exemplo de média geométrica

Depois de vermos a teoria sobre a média geométrica, faremos um exemplo para que você veja exatamente como obter a média geométrica.

Os resultados económicos de uma empresa nos últimos cinco anos são conhecidos. No primeiro ano a empresa gerou uma rentabilidade económica de 10%, no segundo ano o lucro atingiu 23%, no terceiro ano o dinheiro ganho foi de 16%, no quarto ano alcançou uma rentabilidade económica de 7% e o investimento no quinto ano representou um retorno de 20%. Você será solicitado a calcular a média de todas as porcentagens.

Como vimos, para calcular a média dos percentuais não se deve utilizar a média aritmética, mas sim fazer o cálculo com a média geométrica.

Portanto, aplicamos a fórmula da média geométrica:

$MG=\sqrt[n]{\prod_{i=1}^Nx_i}=\sqrt[n]{x_1\cdot x_2\cdot \ldots x_n}$

E substituímos os valores do exemplo na fórmula e realizamos o cálculo:

$MG=\sqrt[5]{1,10\cdot 1,23\cdot 1,16\cdot 1,07\cdot 1,20}=1,15 \ \longrightarrow \ 15 \%$

Observe que temos cinco pontos de dados, portanto estamos calculando a quinta raiz.

O resultado numérico da média geométrica é 1,15, o que significa que a empresa teve um crescimento econômico médio de 15% a cada ano.

Lembre-se que conseguimos obter a média geométrica porque todos os valores eram positivos, mas se alguma porcentagem fosse negativa teríamos que colocar os dados na fórmula como um decimal positivo com a parte inteira. igual a zero. Por exemplo, um crescimento de -30% deve ser expresso na fórmula como 0,70 (1-0,3=0,7).

Calculadora de Média Geométrica

Insira qualquer estatística de amostra na calculadora abaixo para encontrar sua média geométrica. Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal. Lembre-se de que você não pode determinar a média geométrica se um valor for negativo ou zero.

Propriedades da média geométrica

A média geométrica possui as seguintes características:

Este é um tipo de média muito útil para encontrar a média de percentagens ou índices.

Só pode ser calculado se todos os dados forem positivos.

O significado geométrico da média geométrica de dois números a e b é o lado de um quadrado com a mesma área do retângulo cujos lados medem a e b .

$MG(a,b)=\sqrt{a\cdot b}$

O significado geométrico da média geométrica de três números a , b e c é o lado de um cubo cujo volume equivale ao paralelepípedo dos lados a , b e c .

$MG(a,b,c)=\sqrt[3]{a\cdot b \cdot c}$

O logaritmo da média geométrica de um conjunto de dados fornece a média aritmética dos logaritmos do mesmo conjunto.

A média geométrica de um conjunto de valores será sempre menor ou igual à média aritmética.

$\sqrt[N]{x_1\cdot x_2\ldots x_N}\leq \cfrac{x_1+x_2+\ldots+x_N}{N}$

A média geométrica ponderada é calculada da mesma forma que a média geométrica, mas adicionando pesos ao expoente de cada item de dados para ponderar os valores estatísticos.

$\displaystyle \left(\prod_{i=1}^n{x_i}^{\alpha_i}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}} \left}}$

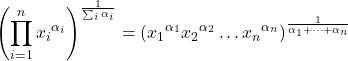
Calcular média geométrica no Excel

Por fim, vamos ver como encontrar a média geométrica de um conjunto de dados usando o programa Excel.

Para calcular a média geométrica no Excel, você precisa usar a função MEANS.GEOM. Basta inserir todos os valores dos quais deseja obter a média geométrica e a função retornará o resultado da média geométrica.

Por exemplo, para determinar a média geométrica do exemplo trabalhado acima, você deve escrever em uma caixa do Excel =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) .

Você deve ter em mente que se algum dos valores for zero ou negativo, a função retornará um erro.

Como você pode ver, é muito mais simples e rápido calcular uma média geométrica no Excel, pois basta copiar os dados para uma planilha e utilizar uma fórmula.

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais