Média harmônica

Aqui explicamos o que é a média harmônica e como ela é calculada (fórmula). Além disso, calculamos a média harmônica de um exemplo passo a passo. Você também encontrará uma calculadora para calcular a média harmônica de qualquer conjunto de dados. E finalmente, você poderá ver quais são as propriedades da média harmônica.

Qual é a média harmônica?

A média harmônica é uma medida de posição central da estatística descritiva. A média harmônica é calculada dividindo o número total de dados estatísticos pela soma dos recíprocos de cada valor.

A média harmônica é usada para calcular velocidades médias, tempos ou fazer cálculos eletrônicos. Este recurso diferencia a média harmônica de outros tipos de médias, frequentemente utilizadas no cálculo de preços médios ou percentuais.

Portanto, a fórmula da média harmônica é a seguinte:

A média harmônica é geralmente representada por um H maiúsculo.

Outros tipos de média que existem são a média aritmética, a média ponderada, a média quadrada e a média geométrica. A média harmônica apresenta vantagens e desvantagens em relação a outros tipos de média, a seguir veremos quais são.

Como calcular a média harmônica

Para calcular a média harmônica, devem ser executados os seguintes passos:

1. Calcule o inverso de cada dado estatístico da amostra.
2. Adicione todos os inversos calculados.
3. Divida o número total de dados pela soma encontrada na etapa anterior.
4. O resultado obtido é a média harmônica da amostra estatística.

👉 Como você pode ver, calcular a média harmônica de um conjunto de dados requer muitas operações, por isso é bastante trabalhoso fazer isso manualmente. Portanto, para calcular a média harmônica, recomendamos utilizar a calculadora abaixo.

Exemplo de média harmônica

Depois de ver a teoria sobre a média harmônica, veremos como encontrar a média harmônica de um conjunto de dados resolvendo passo a passo o exemplo do preço de uma ação.

• Uma pessoa compra ações de uma empresa todos os anos durante 5 anos consecutivos. Durante este período, o preço das ações oscilou muito: no primeiro ano cada ação valia 7€, no segundo ano 10€, no terceiro ano 15€, no quarto ano a empresa sofreu perdas financeiras significativas e o o preço caiu para 6 euros por ação e, eventualmente, no quinto ano, a empresa fez um grande investimento que elevou o preço para 11 euros. Qual foi o preço médio de compra das ações?

Uma opção seria calcular a média aritmética, ou seja, somar todos os preços e dividir por cinco. Porém, como as compras foram realizadas em anos diferentes, calcular a média aritmética seria um erro. Devemos, portanto, encontrar a média harmônica de todos os preços.

A seguir, aplicamos a fórmula da média harmônica:

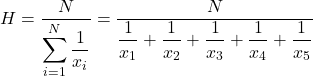
E então substituímos os valores de preços problemáticos na fórmula e calculamos a média harmônica:

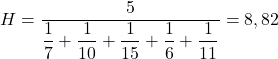
Você tem que colocar cinco no numerador da fração porque existem cinco informações diferentes.

Assim, o preço médio das ações que adquiriu neste período é de 8,82 euros por ação.

Calculadora de Média Harmônica

Com a calculadora a seguir você pode calcular a média harmônica de qualquer conjunto de dados estatísticos.

Você deve inserir números usando o ponto como separador decimal e separar os números com um espaço. Lembre-se que para encontrar a média harmônica nenhum valor pode ser zero.

Propriedades da média harmônica

A média harmônica possui as seguintes características:

• Valores grandes têm pouco efeito na média harmônica de um conjunto, ou seja, um valor muito grande em relação a outros dados não causará uma mudança perceptível na média harmônica.

• Por outro lado, um valor pequeno influencia muito a média harmônica de um conjunto, reduzindo significativamente o seu valor. Na verdade, os recíprocos do denominador da fórmula assumem valores muito grandes.

• A média harmônica não pode ser calculada se algum dos dados for zero, pois isso causaria indeterminação na fórmula. Nesse caso, a média harmônica é considerada indefinida.

• O recíproco da média harmônica é equivalente à média aritmética dos recíprocos das observações.

• Para o mesmo grupo de dados, a média harmônica será menor ou igual à média aritmética.

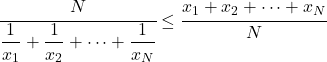
Calcule a média harmônica com Excel

Como vimos, calcular manualmente a média harmônica pode ser bastante tedioso porque muitos cálculos precisam ser realizados. E fica ainda mais complicado quando você tem uma grande quantidade de dados. Portanto, para encontrar a média harmônica, recomendamos o uso de uma calculadora ou do programa Excel.

A média harmônica no Excel é calculada com a fórmula MEAN.ARMO . Ou seja, para calcular a média harmônica de um conjunto de dados, é necessário copiá-los para uma planilha Excel e inserir todos os dados na função MEAN.ARMO .

Por exemplo, para obter a média harmônica do exercício que resolvemos acima, você escreve em uma célula do Excel =MEDIA.ARMO(7;10;15;6;11) .

Você deve ter em mente que se algum dos valores for zero, a função retornará um erro, pois a média harmônica de um conjunto de valores estatísticos não pode ser determinada se algum deles for zero.