Média ponderada

By Dr. benjamim anderson Agosto 6, 2023 Estatisticas 0 Comments

Aqui explicamos o que é a média ponderada e como ela é calculada. Você poderá ver um exercício resolvido sobre como encontramos a média ponderada. E, além do mais, você pode calcular a média ponderada de qualquer conjunto de dados com a calculadora no final.

Qual é a média ponderada?

A média ponderada é uma medida da centralidade das estatísticas descritivas. Para calcular a média ponderada, você deve primeiro multiplicar cada dado estatístico pelo seu peso (ou peso), depois somar todos os produtos e, por fim, dividir a soma ponderada pela soma de todos os pesos.

Em outras palavras, a fórmula da média ponderada é a seguinte:

Onde x _i representa cada amostra de dados e w _i seu peso correspondente.

Assim, quanto maior o peso de um dado, mais importante ele se torna no cálculo da média ponderada. Ou seja, quanto maior o peso de um dado, mais ele influenciará o resultado da média ponderada.

A média ponderada é particularmente útil para o cálculo de notas, pois permite avaliar com diferentes importâncias os exercícios ou exames realizados durante um curso. A média ponderada também é utilizada para calcular o IPC (Índice de Preços ao Consumidor), que é um indicador para medir os preços de uma população.

Além da média ponderada, existem também outros tipos de médias, como média geométrica, média aritmética, média quadrada e média harmônica.

Como calcular a média ponderada

Para calcular a média ponderada, devem ser seguidos os seguintes passos:

Multiplique cada dado estatístico pelo seu peso correspondente.
Some todos os produtos calculados na etapa anterior.
Divida a soma ponderada acima pela soma de todos os pesos.
O resultado obtido é a média ponderada da amostra estatística.

👉 Você pode usar a calculadora abaixo para calcular a média ponderada de qualquer conjunto de dados.

Exemplo de média ponderada

Considerando a definição de média ponderada, resolveremos agora um exercício para compreender completamente como a média ponderada é obtida a partir de um conjunto de dados.

Um aluno do 1.º ano do ensino secundário obteve as seguintes classificações na disciplina de matemática: 7 no exame parcial que vale 30%, 9 no trabalho de grupo que vale 20%, 6 nos exercícios dados em aula com ponderação de 10% e nota 8 no exame final que tem uma ponderação de 40%. Qual a sua nota final na matéria?

Para determinar a nota do aluno, é necessário encontrar a média ponderada com os valores dados pelo enunciado. Para fazer isso, aplicamos a fórmula da média ponderada:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

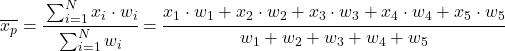
A pontuação de cada entrega é o valor estatístico e a sua percentagem corresponde ao peso desse valor. Portanto, substituímos os valores e pesos na fórmula e realizamos o cálculo da média ponderada:

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

A nota final de matemática deste aluno será, portanto, 7,7 porque este é o resultado obtido a partir da média ponderada.

Calculadora de média ponderada

Insira os dados de qualquer amostra estatística e seus respectivos pesos na calculadora abaixo para calcular sua média ponderada.

Insira os dados estatísticos na primeira caixa e seus respectivos pesos na segunda caixa. Você deve escrever os pesos na mesma ordem dos dados e em formato decimal. Todos os números devem ser separados por um espaço e inseridos usando o ponto final como separador decimal.

Pesos padronizados

Como vimos, na média ponderada, o peso é o valor que se atribui a cada dado para lhe dar maior ou menor importância. Então, se a informação for muito importante terá um peso muito alto, mas se a informação não for muito relevante terá um peso muito baixo.

Pois bem, o peso normalizado é um tipo de ponderação utilizada para obter a média ponderada sem a necessidade de fazer nenhuma divisão.

O peso normalizado é o peso de um item de dados dividido pela soma de todos os pesos.

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

A soma de todos os pesos normalizados é, portanto, igual a um:

$\sum_{i=1}^N w_i'=1$

Portanto, para calcular a média ponderada com os pesos normalizados , basta multiplicar cada item de dados pelo seu peso normalizado:

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

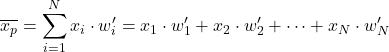
Por exemplo, temos uma amostra estatística cujos dados são 24, 35, 17, 41 e seus respectivos pesos são 4, 9, 6, 3. Para encontrar a média ponderada deste conjunto de dados, podemos primeiro calcular os pesos normalizados dividindo cada peso pela soma de todos os pesos:

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

E agora é só multiplicar cada dado pelo seu peso normalizado e o resultado será a média ponderada:

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

Diferença entre média ponderada e média aritmética

O cálculo da média ponderada e da média aritmética é feito da mesma forma, pois devem ser realizadas operações semelhantes. Na média ponderada, cada ponto de dados é multiplicado pelo seu peso e dividido pela soma dos pesos, mas na média aritmética, todos os dados são somados e divididos pelo número total de pontos de dados.

A diferença entre a média ponderada e a média aritmética está no seu conceito, pois na média aritmética considera-se que todos os dados possuem o mesmo valor, porém, na média ponderada cada dado possui um peso diferente.

Observe que se todos os pesos forem iguais, a média ponderada equivale à média aritmética. Você pode ver a prova matemática abaixo:

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais