As três suposições de medidas repetidas anova

Uma ANOVA de medidas repetidas é usada para determinar se há ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos em que os mesmos sujeitos aparecem em cada grupo.

No entanto, antes de realizar uma ANOVA de medidas repetidas, devemos garantir que as seguintes suposições sejam atendidas:

1. Independência: Cada observação deve ser independente.

2. Normalidade: A distribuição da variável resposta é normalmente distribuída.

3. Esfericidade: As variâncias das diferenças entre todas as combinações de grupos relacionados devem ser iguais.

Se uma ou mais destas suposições forem violadas, os resultados da ANOVA de medidas repetidas podem não ser confiáveis.

Neste artigo, fornecemos uma explicação para cada suposição, como determinar se a suposição foi atendida e o que fazer se não for atendida.

Hipótese 1: Independência

Uma medida ANOVA repetida pressupõe que cada observação no seu conjunto de dados é independente de todas as outras observações.

Como determinar se essa suposição é atendida

A maneira mais simples de verificar esta suposição é verificar se cada indivíduo no conjunto de dados foi amostrado aleatoriamente da população usando um método de amostragem aleatória .

Se um método de amostragem aleatória for usado, cada observação pode ser considerada independente.

O que fazer se esta suposição não for respeitada

Se esta suposição não for atendida, então é um problema sério porque os valores de cada indivíduo podem estar relacionados entre si de uma forma ou de outra.

Muitas vezes, a única solução neste cenário é recrutar indivíduos para um novo estudo utilizando um método de amostragem aleatória.

Hipótese 2: normalidade

Uma medida ANOVA repetida assume que a distribuição da variável de resposta é normalmente distribuída .

Como determinar se essa suposição é atendida

Existem duas maneiras de verificar se esta hipótese é verdadeira:

1. Crie um histograma ou gráfico QQ

Você pode verificar visualmente se a distribuição da variável de resposta tem distribuição aproximadamente normal criando um histograma ou gráfico QQ.

Se você criar um histograma , basta verificar se a distribuição da variável de resposta segue aproximadamente o formato de um “sino”. Nesse caso, muitas vezes você pode assumir que a suposição de normalidade foi atendida:

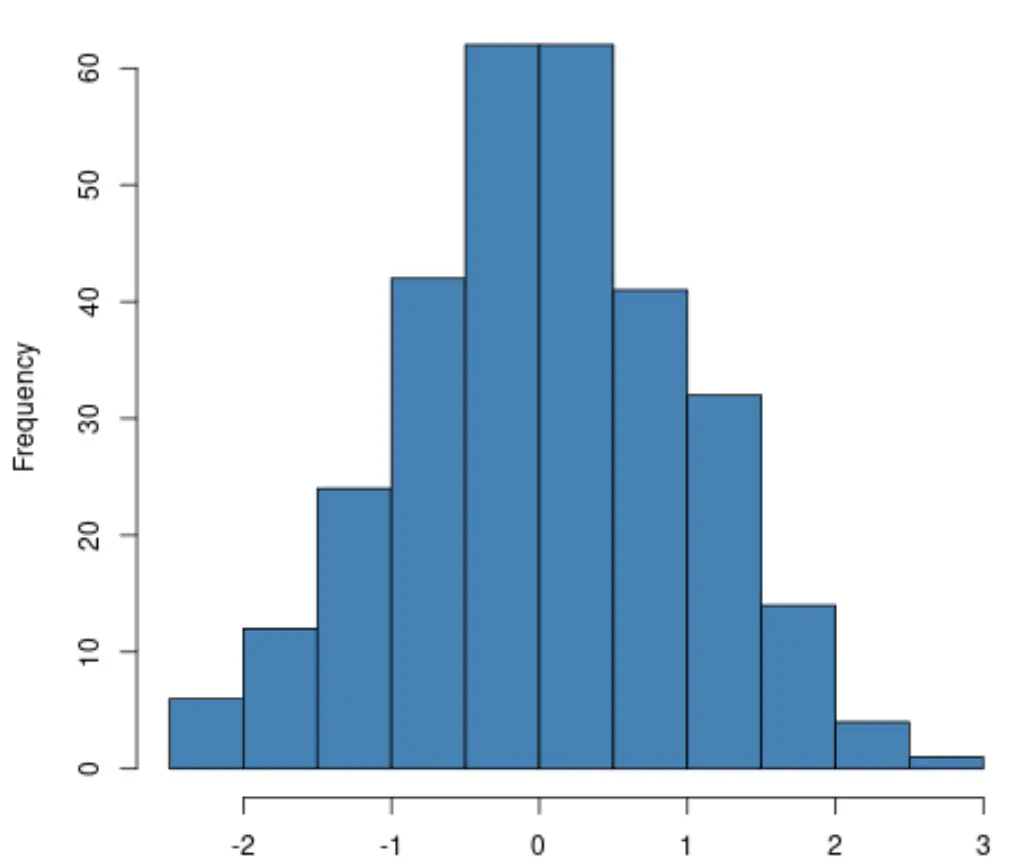
Se você estiver criando um gráfico QQ , verifique se os pontos de dados estão ao longo de uma linha reta diagonal. Nesse caso, geralmente você pode assumir que a suposição de normalidade foi atendida:

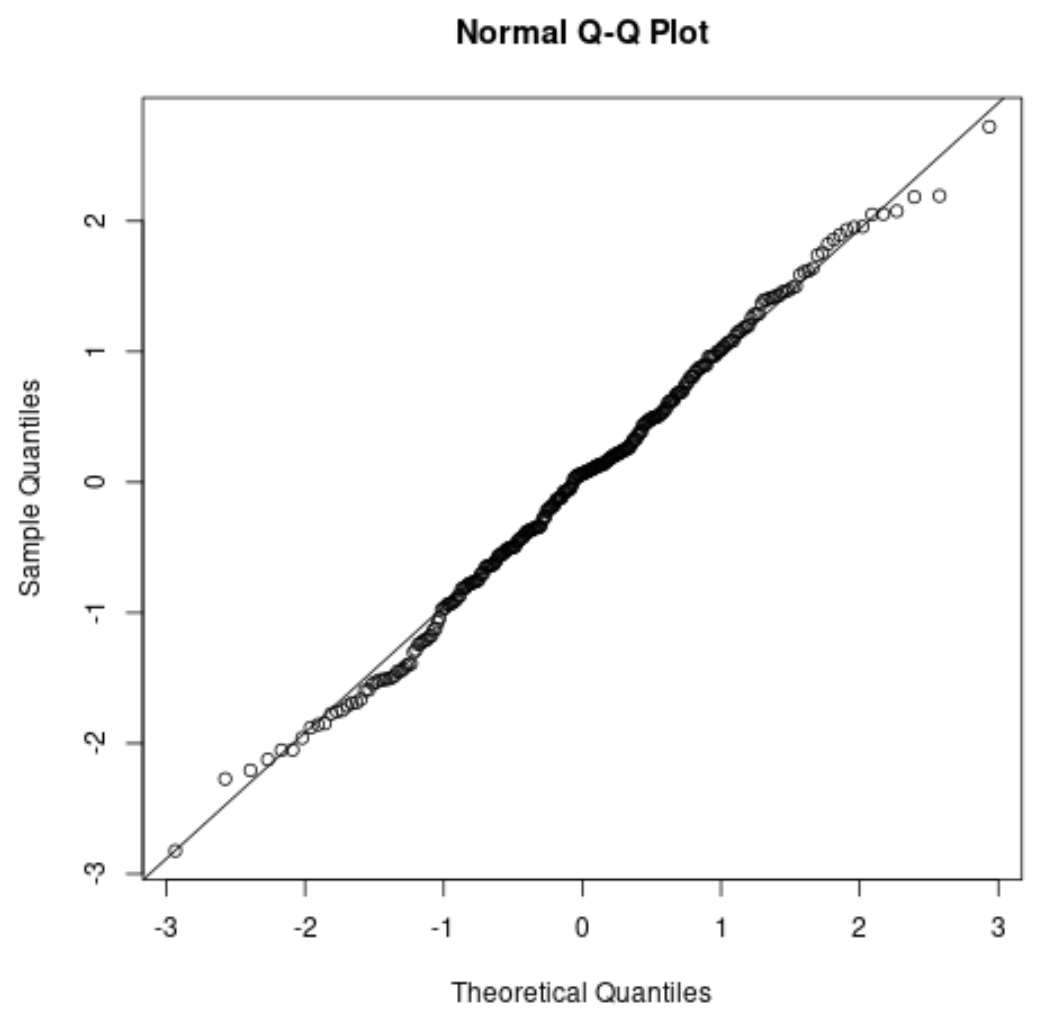
Relacionado: Como usar gráficos QQ para verificar a normalidade

2. Realize um teste estatístico formal

Você também pode realizar um teste de Shapiro-Wilk para verificar a normalidade. Se o valor p do teste for inferior a 0,05, sugere que os dados não têm distribuição normal.

No entanto, esteja ciente de que, ao trabalhar com amostras extremamente grandes, testes estatísticos como o teste de Shapiro-Wilk quase sempre dirão que seus dados não são normais.

Por esse motivo, geralmente é melhor inspecionar visualmente seus dados usando gráficos como histogramas e gráficos QQ. Apenas olhando os gráficos você pode ter uma boa ideia se os dados estão normalmente distribuídos ou não.

O que fazer se esta suposição não for respeitada

Em geral, uma ANOVA de medidas repetidas é considerada bastante robusta contra violações da suposição de normalidade, desde que os tamanhos das amostras sejam grandes o suficiente.

Se a suposição de normalidade for gravemente violada, você terá duas opções:

1. Transforme os valores de resposta dos seus dados para que as distribuições sejam distribuídas de forma mais normal.

2. Realize um teste não paramétrico equivalente, como o teste de Friedman , que não requer a suposição de normalidade.

Suposição 3: Esfericidade

Uma ANOVA de medidas repetidas assume esfericidade – isto é, as variâncias das diferenças entre todas as combinações de grupos relacionados devem ser iguais.

Se esta suposição não for atendida, o índice F torna-se inflacionado e os resultados de medidas repetidas ANOVA tornam-se não confiáveis.

Como determinar se essa suposição é atendida

Para testar se esta suposição é atendida, podemos realizar o teste de esfericidade de Mauchly.

Este teste utiliza a seguinte hipótese nula e alternativa:

• H ₀ : As variâncias das diferenças são iguais
• _HA : As variâncias das diferenças não são iguais

Se o valor p do teste estiver abaixo de um certo nível de significância (por exemplo, α = 0,05), então rejeitamos a hipótese nula e concluímos que as variâncias das diferenças não são iguais.

Caso contrário, se o valor p não for inferior a um certo nível de significância (por exemplo, α = 0,05), não rejeitamos a hipótese nula e concluímos que a suposição de esfericidade é satisfeita.

Dependendo do software estatístico que você usa, os resultados deste teste serão assim:

Como o valor p não é inferior a 0,05, não rejeitaremos a hipótese nula e concluiremos que a suposição de esfericidade é atendida neste exemplo específico.

O que fazer se esta suposição não for respeitada

Se rejeitarmos a hipótese nula do teste de esfericidade de Mauchly, geralmente aplicamos uma correção aos graus de liberdade usados para calcular o valor F na tabela ANOVA de medidas repetidas.

Existem três correções que podemos aplicar:

• Huynh-Feldt (menos conservador)
• Serre-Geisser
• Limite inferior (mais conservador)

Cada uma dessas correções tende a aumentar os valores de p na tabela de resultados da ANOVA de medidas repetidas para levar em conta o fato de que a suposição de esfericidade é violada.

Podemos então usar esses valores de p para determinar se devemos ou não rejeitar a hipótese nula de ANOVA de medidas repetidas.

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre ANOVA de medidas repetidas:

Uma introdução à ANOVA de medidas repetidas
Calculadora ANOVA de Medidas Repetidas
Como relatar os resultados de uma ANOVA de medidas repetidas
ANOVA unidirecional e ANOVA de medidas repetidas: a diferença