Como usar o método elbow em python para encontrar clusters ideais

Um dos algoritmos de clustering mais comuns em aprendizado de máquina é conhecido como clustering k-means .

O agrupamento K-means é uma técnica na qual colocamos cada observação de um conjunto de dados em um dos K clusters.

O objetivo final é ter K clusters nos quais as observações dentro de cada cluster sejam bastante semelhantes entre si, enquanto as observações em diferentes clusters sejam bastante diferentes umas das outras.

Ao fazer clustering k-means, o primeiro passo é escolher um valor para K – o número de clusters nos quais queremos colocar as observações.

Uma das maneiras mais comuns de escolher um valor para K é conhecida como método do cotovelo , que envolve a criação de um gráfico com o número de clusters no eixo x e o total na soma dos quadrados no eixo y e, em seguida, identificar onde aparece um “joelho” ou giro na trama.

O ponto no eixo x onde ocorre o “joelho” nos indica o número ideal de clusters a serem usados no algoritmo de agrupamento k-means.

O exemplo a seguir mostra como usar o método cotovelo em Python.

Passo 1: Importe os módulos necessários

Primeiro, importaremos todos os módulos necessários para realizar o clustering k-means:

 import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler

Etapa 2: Crie o DataFrame

A seguir, criaremos um DataFrame contendo três variáveis para 20 jogadores de basquete diferentes:

 #createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
                              35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
                   ' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
                               np.nan, 9, 4, 3, 4, 12, 15, 11],
                   ' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
                                11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})

#drop rows with NA values in any columns
df = df. dropna ()

#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)

Etapa 3: use o método Elbow para encontrar o número ideal de clusters

Digamos que queremos usar clustering k-means para agrupar atores semelhantes com base nessas três métricas.

Para realizar clustering k-means em Python, podemos usar a função KMeans do módulo sklearn .

O argumento mais importante para esta função é n_clusters , que especifica em quantos clusters colocar as observações.

Para determinar o número ideal de clusters, criaremos um gráfico que exibe o número de clusters, bem como o SSE (soma dos erros quadráticos) do modelo.

Procuraremos então um “joelho” onde a soma dos quadrados começa a “dobrar” ou estabilizar. Este ponto representa o número ideal de clusters.

O código a seguir mostra como criar esse tipo de gráfico que exibe o número de clusters no eixo x e o SSE no eixo y:

 #initialize kmeans parameters
kmeans_kwargs = {
" init ": " random ",
" n_init ": 10,
" random_state ": 1,
}

#create list to hold SSE values for each k
sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, ** kmeans_kwargs)
    kmeans. fit (scaled_df)
    sse. append (kmeans.inertia_)

#visualize results
plt. plot (range(1, 11), sse)
plt. xticks (range(1, 11))
plt. xlabel (" Number of Clusters ")
plt. ylabel (“ SSE ”)
plt. show () 

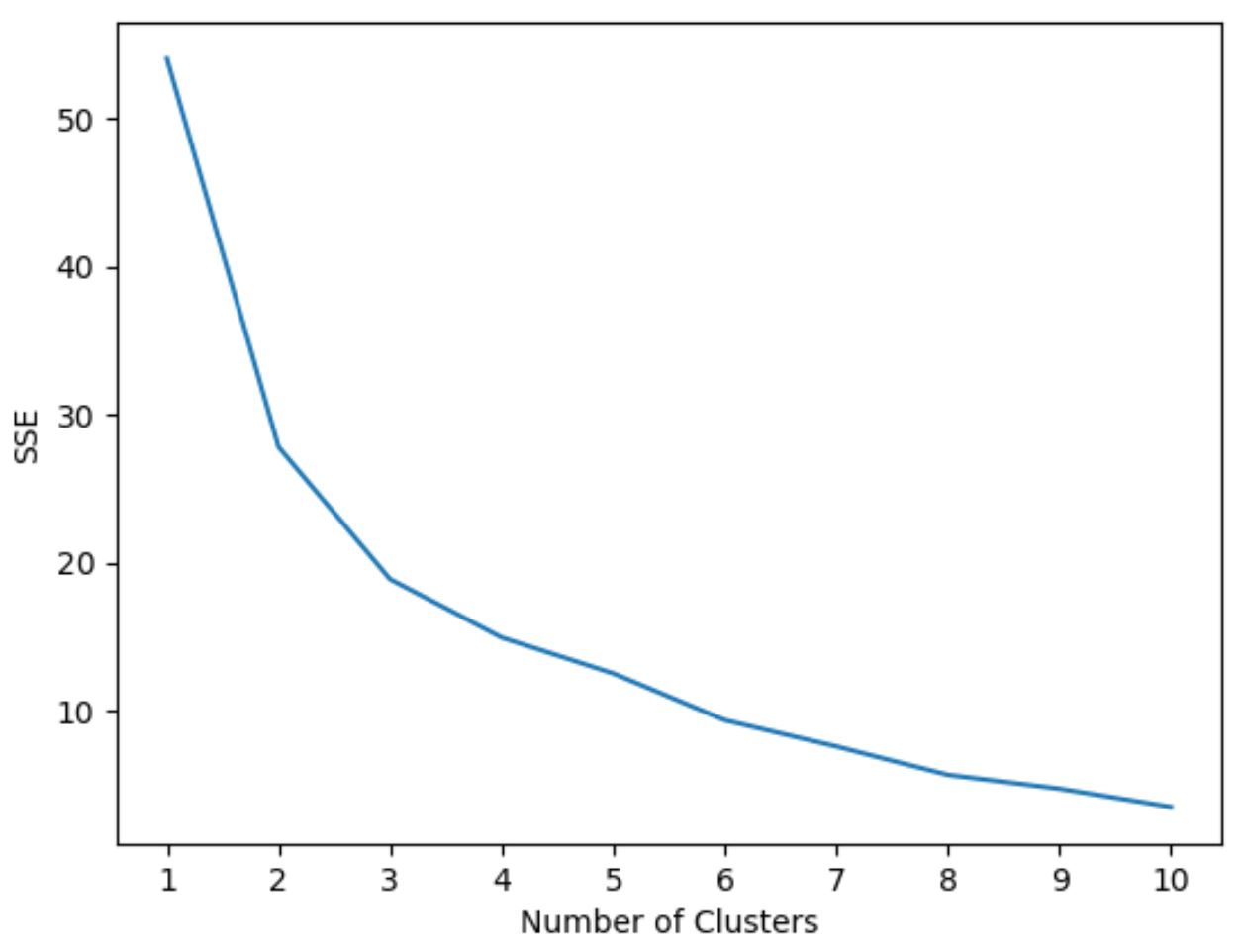
Neste gráfico, parece que há uma torção ou “joelho” em k = 3 clusters .

Portanto, usaremos 3 clusters ao ajustar nosso modelo de cluster k-means na próxima etapa.

Etapa 4: realizar clustering K-Means com K ideal

O código a seguir mostra como realizar clustering k-means no conjunto de dados usando o valor ideal para k de 3:

 #instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )

#fit k-means algorithm to data
kmeans. fit (scaled_df)

#view cluster assignments for each observation
kmeans. labels_

array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0]) 

A tabela resultante mostra as atribuições de cluster para cada observação no DataFrame.

Para facilitar a interpretação desses resultados, podemos adicionar uma coluna ao DataFrame que mostra a atribuição de cluster de cada jogador:

 #append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_

#view updated DataFrame
print (df)

points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0

A coluna do cluster contém um número de cluster (0, 1 ou 2) ao qual cada jogador foi atribuído.

Jogadores pertencentes ao mesmo cluster possuem valores aproximadamente semelhantes para as colunas de pontos , assistências e rebotes .

Nota : Você pode encontrar a documentação completa da função KMeans do sklearn aqui .

Recursos adicionais

Os tutoriais a seguir explicam como realizar outras tarefas comuns em Python:

Como realizar regressão linear em Python
Como realizar regressão logística em Python
Como realizar a validação cruzada K-Fold em Python