Como usar o método dos mínimos quadrados em r
O método dos mínimos quadrados é um método que podemos usar para encontrar a linha de regressão que melhor se ajusta a um determinado conjunto de dados.
Para usar o método dos mínimos quadrados para ajustar uma linha de regressão em R, podemos usar a função lm() .
Esta função usa a seguinte sintaxe básica:
model <- lm(response ~ predictor, data=df)
O exemplo a seguir mostra como usar esta função em R.
Exemplo: método dos mínimos quadrados em R
Suponha que temos o seguinte quadro de dados em R que mostra o número de horas estudadas e a nota do exame correspondente para 15 alunos em uma turma:
#create data frame df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14), score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89)) #view first six rows of data frame head(df) hours score 1 1 64 2 2 66 3 4 76 4 5 73 5 5 74 6 6 81
Podemos usar a função lm() para usar o método dos mínimos quadrados para ajustar uma linha de regressão a estes dados:
#use method of least squares to fit regression line model <- lm(score ~ hours, data=df) #view regression model summary summary(model) Call: lm(formula = score ~ hours, data = df) Residuals: Min 1Q Median 3Q Max -5,140 -3,219 -1,193 2,816 5,772 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 65,334 2,106 31,023 1.41e-13 *** hours 1.982 0.248 7.995 2.25e-06 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.641 on 13 degrees of freedom Multiple R-squared: 0.831, Adjusted R-squared: 0.818 F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06
A partir dos valores da coluna Resultado Estimado , podemos escrever a seguinte linha de regressão ajustada:
Nota do exame = 65,334 + 1,982 (horas)
Veja como interpretar cada coeficiente no modelo:
- Interceptação : Para um aluno que estuda 0 horas, a nota esperada do exame é 65,334 .
- horas : Para cada hora adicional estudada, a nota esperada do exame aumenta em 1.982 .
Podemos usar essa equação para estimar a nota do exame que um aluno receberá com base nas horas estudadas.
Por exemplo, se um aluno estudar 5 horas, estimaríamos que sua nota no exame seria 75,244:
Nota do exame = 65,334 + 1,982(5) = 75,244
Finalmente, podemos criar um gráfico de dispersão dos dados originais com a linha de regressão ajustada sobreposta ao gráfico:
#create scatter plot of data plot(df$hours, df$score, pch=16, col=' steelblue ') #add fitted regression line to scatter plot abline(model)
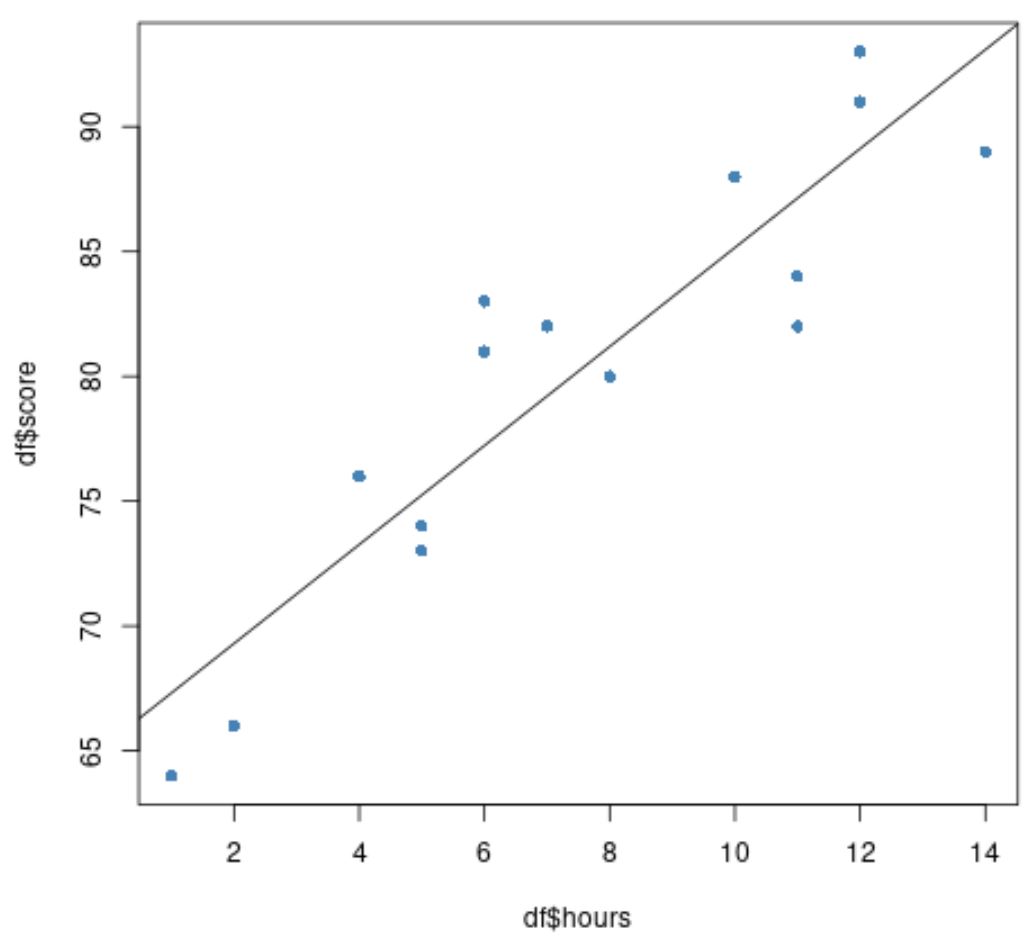
Os círculos azuis representam os dados e a linha preta representa a linha de regressão ajustada.
Recursos adicionais
Os tutoriais a seguir explicam como realizar outras tarefas comuns em R:
Como criar um gráfico residual em R
Como testar a multicolinearidade em R
Como realizar ajuste de curva em R