Mínimos quadrados parciais em r (passo a passo)

Um dos problemas mais comuns que você encontrará no aprendizado de máquina é a multicolinearidade . Isso ocorre quando duas ou mais variáveis preditoras em um conjunto de dados estão altamente correlacionadas.

Quando isso acontece, um modelo pode ser capaz de ajustar bem um conjunto de dados de treinamento, mas pode ter um desempenho ruim em um novo conjunto de dados que nunca viu, porque se ajusta demais ao conjunto de dados de treinamento. conjunto de treinamento.

Uma maneira de contornar esse problema é usar um método chamado mínimos quadrados parciais , que funciona da seguinte maneira:

• Padronize variáveis preditoras e de resposta.
• Calcule M combinações lineares (chamadas de “componentes PLS”) das p variáveis preditoras originais que explicam uma quantidade significativa de variação tanto na variável de resposta quanto nas variáveis preditoras.
• Use o método dos mínimos quadrados para ajustar um modelo de regressão linear usando os componentes PLS como preditores.
• Use a validação cruzada k-fold para encontrar o número ideal de componentes PLS a serem mantidos no modelo.

Este tutorial fornece um exemplo passo a passo de como realizar mínimos quadrados parciais em R.

Passo 1: Carregue os pacotes necessários

A maneira mais fácil de realizar mínimos quadrados parciais em R é usar funções no pacote pls .

 #install pls package (if not already installed)
install.packages(" pls ")

load pls package
library(pls)

Etapa 2: Ajustar o modelo de mínimos quadrados parciais

Para este exemplo, usaremos o conjunto de dados R integrado chamado mtcars , que contém dados sobre diferentes tipos de carros:

 #view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1

Para este exemplo, ajustaremos um modelo de mínimos quadrados parciais (PLS) usando hp como variável de resposta e as seguintes variáveis como variáveis preditoras:

• mpg
• mostrar
• merda
• peso
• qsec

O código a seguir mostra como ajustar o modelo PLS a esses dados. Observe os seguintes argumentos:

• scale=TRUE : diz a R que cada uma das variáveis no conjunto de dados deve ser dimensionada para ter uma média de 0 e um desvio padrão de 1. Isso garante que nenhuma variável preditora tenha muita influência no modelo se medida em unidades diferentes.
• validação=”CV” : diz ao R para usar a validação cruzada k-fold para avaliar o desempenho do modelo. Observe que isso usa k=10 dobras por padrão. Observe também que você pode especificar “LOOCV” para realizar a validação cruzada Leave-One-Out .

 #make this example reproducible
set.seed(1)

#fit PCR model
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")

Etapa 3: Escolha o número de componentes PLS

Depois de ajustar o modelo, precisamos determinar quantos componentes PLS manter.

Para fazer isso, basta observar a raiz do erro quadrático médio do teste (teste RMSE) calculado pela validação k-cruzada:

 #view summary of model fitting
summary(model)

Data: 
	Y dimension: 32 1
Fit method: kernelpls
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 40.57 35.48 36.22 36.74 36.67
adjCV 69.66 40.41 35.12 35.80 36.27 36.20

TRAINING: % variance explained
    1 comp 2 comps 3 comps 4 comps 5 comps
X 68.66 89.27 95.82 97.94 100.00
hp 71.84 81.74 82.00 82.02 82.03

Existem duas tabelas interessantes no resultado:

1. VALIDAÇÃO: RMSEP

Esta tabela nos mostra o teste RMSE calculado pela validação cruzada k-fold. Podemos ver o seguinte:

• Se usarmos apenas o termo original no modelo, o RMSE do teste será 69,66 .
• Se adicionarmos o primeiro componente PLS, o teste RMSE cai para 40,57.
• Se adicionarmos o segundo componente PLS, o teste RMSE cai para 35,48.

Podemos ver que a adição de componentes adicionais do PLS resulta, na verdade, em um aumento no RMSE do teste. Assim, parece que seria ótimo usar apenas dois componentes do PLS no modelo final.

2. TREINAMENTO: % de variância explicada

Esta tabela nos informa a porcentagem de variância na variável resposta explicada pelos componentes do PLS. Podemos ver o seguinte:

• Utilizando apenas o primeiro componente do PLS, podemos explicar 68,66% da variação da variável resposta.
• Adicionando o segundo componente do PLS, podemos explicar 89,27% da variação da variável resposta.

Observe que ainda seremos capazes de explicar mais variância usando mais componentes PLS, mas podemos ver que adicionar mais de dois componentes PLS não aumenta muito a porcentagem de variância explicada.

Também podemos visualizar o teste RMSE (junto com o teste MSE e R-quadrado) como uma função do número de componentes do PLS usando a função validaçãoplot() .

 #visualize cross-validation plots
validationplot(model)
validationplot(model, val.type=" MSEP ")
validationplot(model, val.type=" R2 ") 

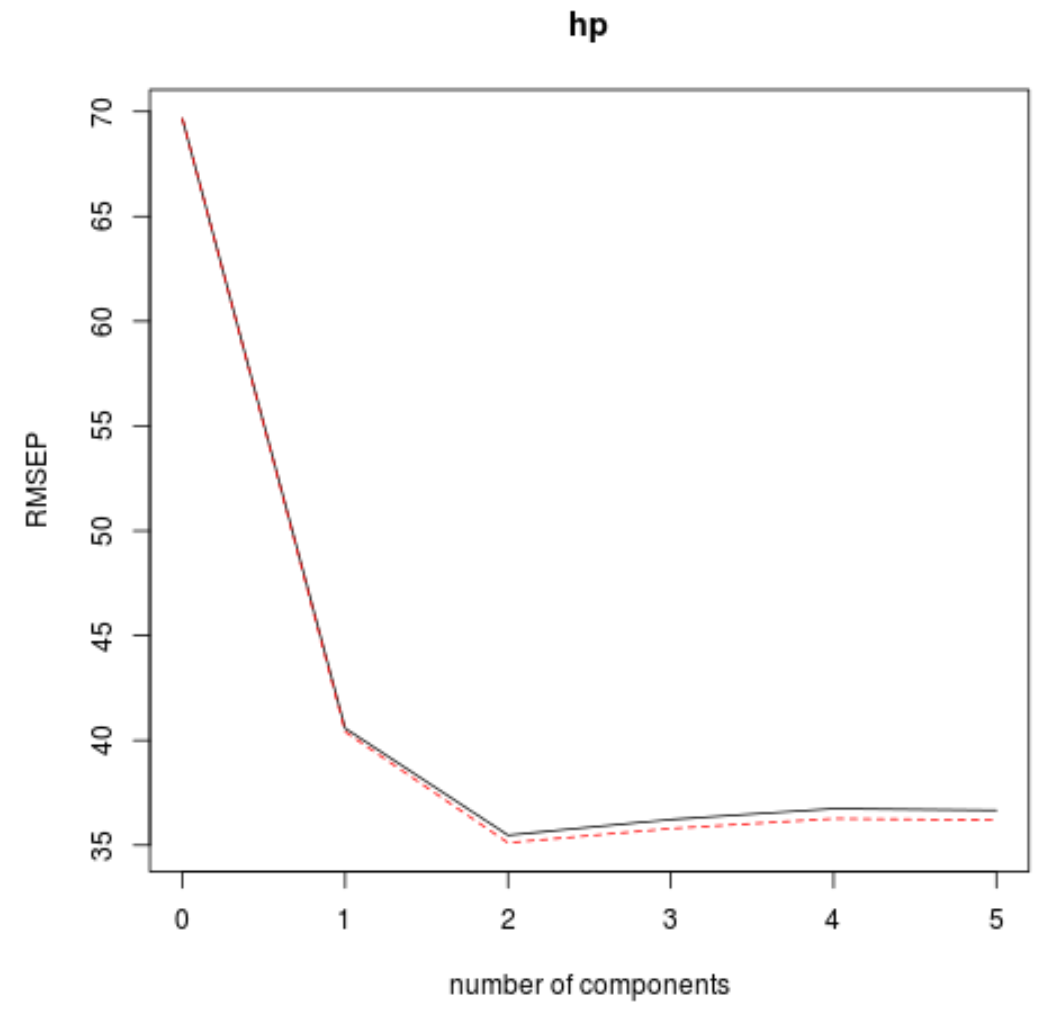
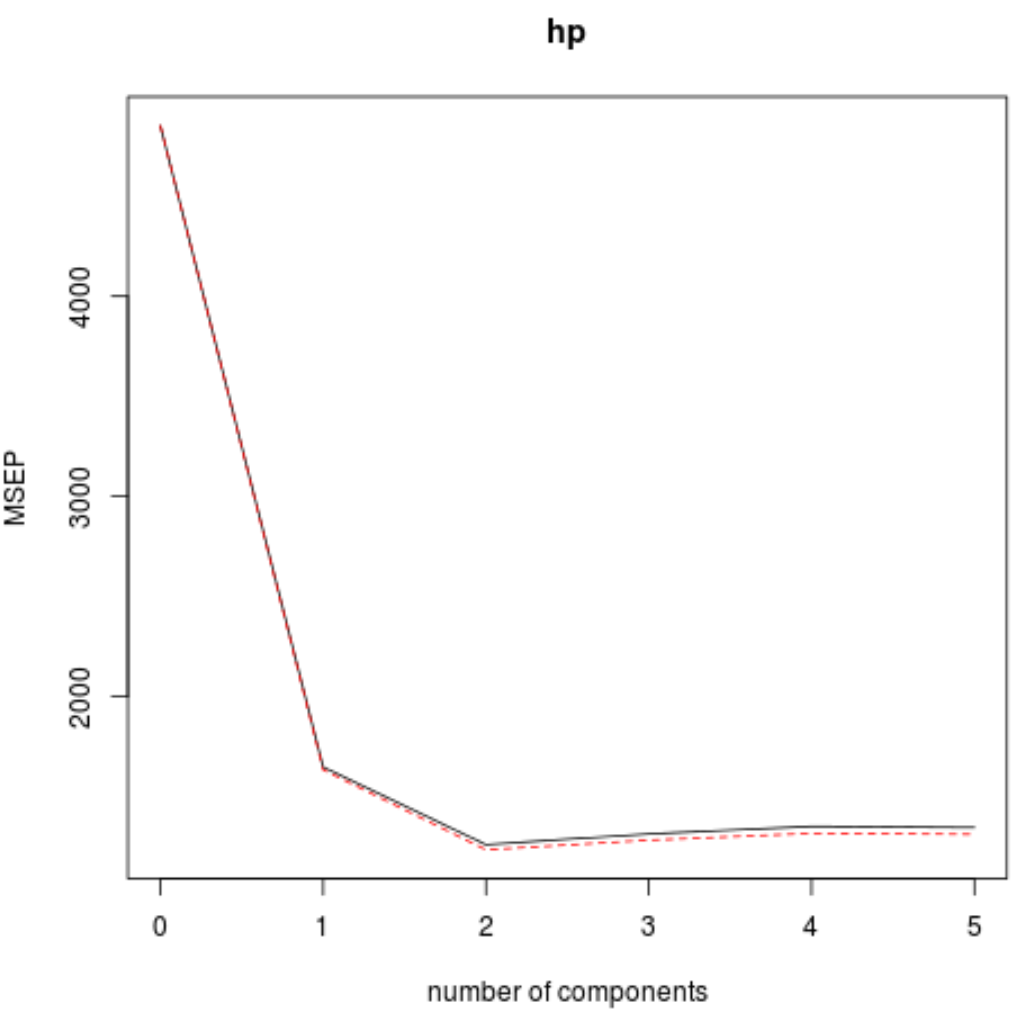
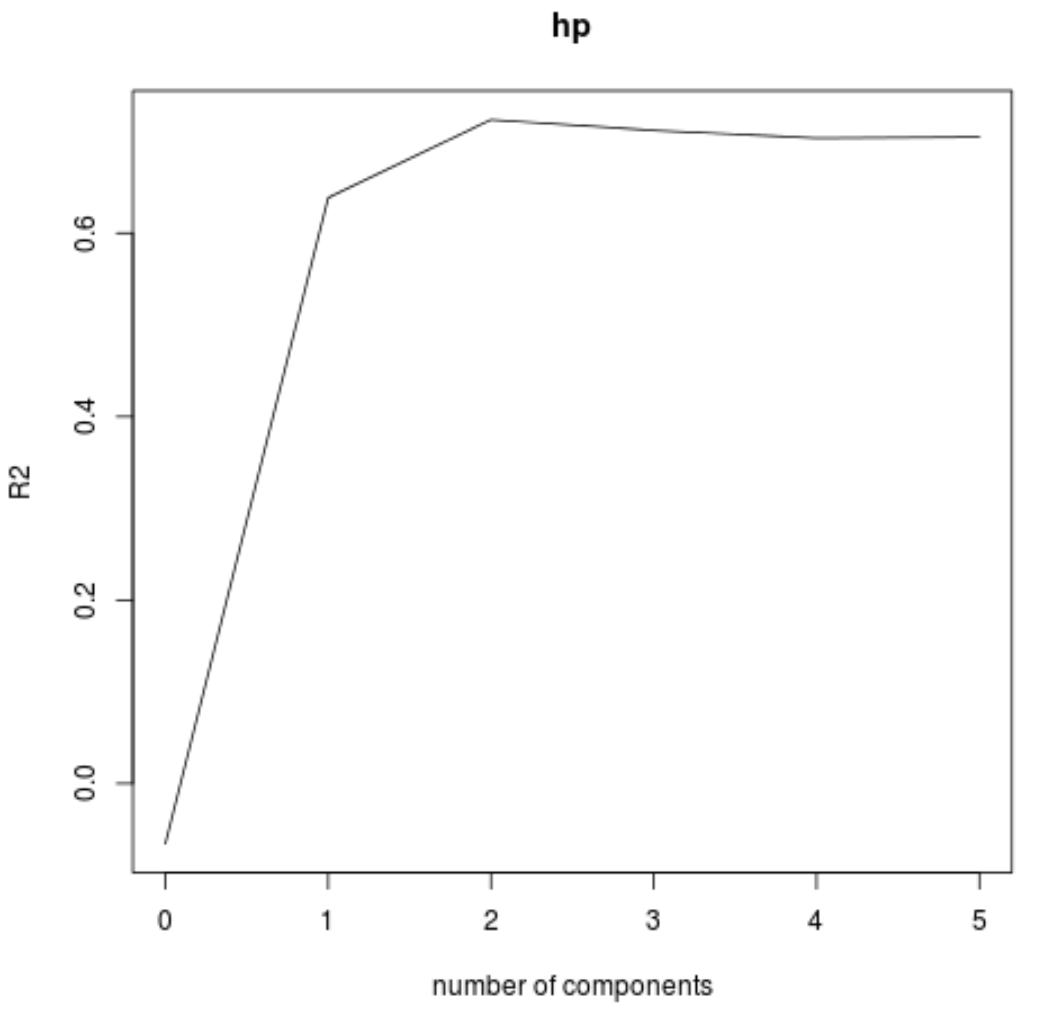
Em cada gráfico, podemos ver que o ajuste do modelo melhora ao adicionar dois componentes PLS, mas tende a piorar quando adicionamos mais componentes PLS.

Assim, o modelo ótimo inclui apenas os dois primeiros componentes do PLS.

Etapa 4: use o modelo final para fazer previsões

Podemos usar o modelo final com dois componentes PLS para fazer previsões sobre novas observações.

O código a seguir mostra como dividir o conjunto de dados original em um conjunto de treinamento e teste e usar o modelo final com dois componentes PLS para fazer previsões no conjunto de teste.

 #define training and testing sets
train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")]
y_test <- mtcars[26: nrow (mtcars), c("hp")]
test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")]
    
#use model to make predictions on a test set
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ")
pcr_pred <- predict(model, test, ncomp= 2 )

#calculate RMSE
sqrt ( mean ((pcr_pred - y_test)^2))

[1] 54.89609

Vemos que o RMSE do teste é 54,89609 . Este é o desvio médio entre o valor de HP previsto e o valor de HP observado para as observações do conjunto de teste.

Observe que um modelo de regressão de componentes principais equivalente com dois componentes principais produziu um teste RMSE de 56,86549 . Assim, o modelo PLS superou ligeiramente o modelo PCR para este conjunto de dados.

O uso completo do código R neste exemplo pode ser encontrado aqui .