Como realizar a regressão de mínimos quadrados ponderados em r

Uma das principais suposições da regressão linear é que os resíduos são distribuídos com variância igual em cada nível da variável preditora. Essa suposição é conhecida como homocedasticidade .

Quando esta suposição não é respeitada, diz-se que a heterocedasticidade está presente nos resíduos. Quando isso acontece, os resultados da regressão tornam-se não confiáveis.

Uma maneira de resolver esse problema é usar a regressão de mínimos quadrados ponderados , que atribui pesos às observações de forma que aquelas com baixa variância de erro recebam mais peso porque contêm mais informações em comparação com observações com maior variância de erro.

Este tutorial fornece um exemplo passo a passo de como realizar regressão de mínimos quadrados ponderados em R.

Etapa 1: crie os dados

O código a seguir cria um quadro de dados contendo o número de horas estudadas e a nota do exame correspondente para 16 alunos:

 df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
                 score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))

Etapa 2: realizar regressão linear

A seguir, usaremos a função lm() para ajustar um modelo de regressão linear simples que usa horas como variável preditora e pontuação como variável de resposta :

 #fit simple linear regression model
model <- lm(score ~ hours, data = df)

#view summary of model
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-17,967 -5,970 -0.719 7,531 15,032 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 60,467 5,128 11,791 1.17e-08 ***
hours 5,500 1,127 4,879 0.000244 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.224 on 14 degrees of freedom
Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 
F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438

Etapa 3: teste de heterocedasticidade

A seguir, criaremos um gráfico dos resíduos e valores ajustados para verificar visualmente a heterocedasticidade:

 #create residual vs. fitted plot
plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

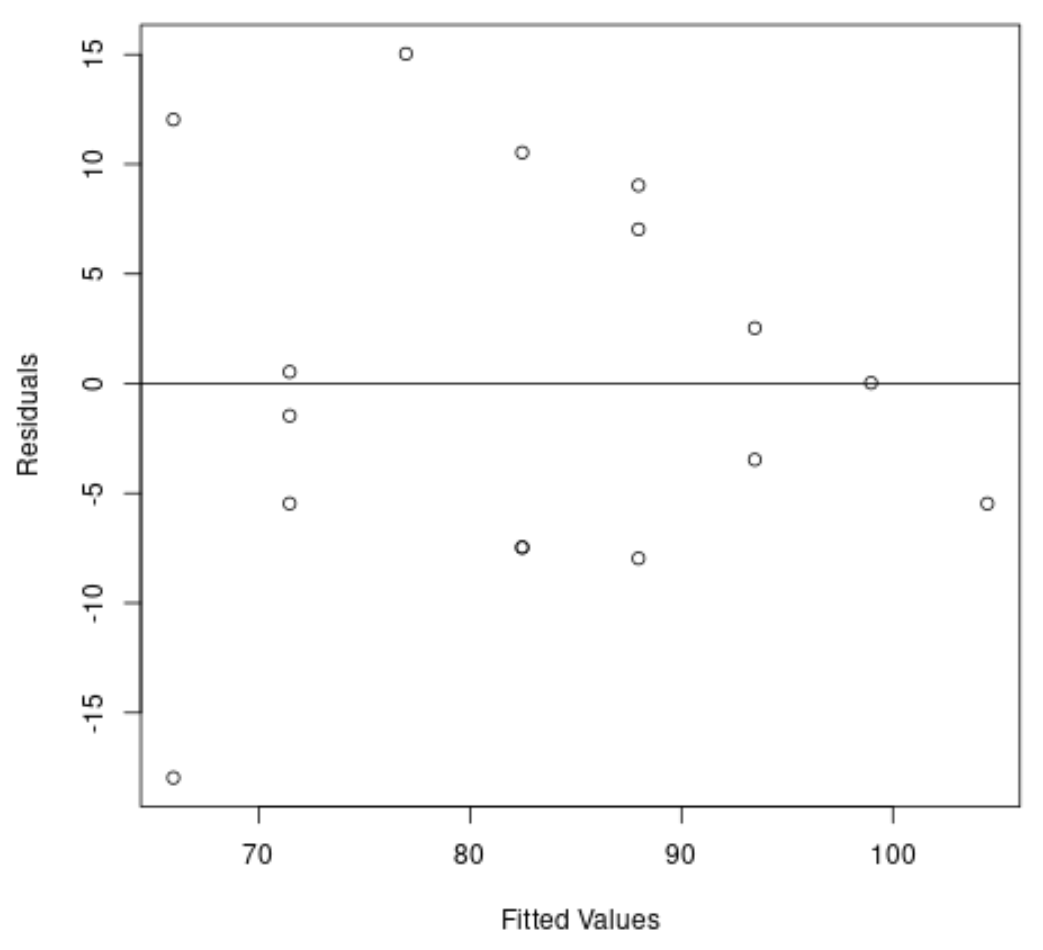
Podemos ver no gráfico que os resíduos têm formato de “cone”: eles não estão distribuídos com variância igual ao longo do gráfico.

Para testar formalmente a heterocedasticidade, podemos realizar um teste de Breusch-Pagan:

 #load lmtest package
library (lmtest)

#perform Breusch-Pagan test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 3.9597, df = 1, p-value = 0.0466

O teste Breusch-Pagan utiliza as seguintes hipóteses nulas e alternativas :

• Hipótese nula (H ₀ ): a homocedasticidade está presente (os resíduos são distribuídos com variância igual)
• Hipótese alternativa ( _HA ): a heterocedasticidade está presente (os resíduos não são distribuídos com variância igual)

Como o valor p do teste é 0,0466 , rejeitaremos a hipótese nula e concluiremos que a heterocedasticidade é um problema neste modelo.

Etapa 4: realizar a regressão de mínimos quadrados ponderados

Como a heterocedasticidade está presente, realizaremos mínimos quadrados ponderados definindo os pesos de forma que as observações com menor variância recebam mais peso:

 #define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2

#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)

#view summary of model
summary(wls_model)

Call:
lm(formula = score ~ hours, data = df, weights = wt)

Weighted Residuals:
    Min 1Q Median 3Q Max 
-2.0167 -0.9263 -0.2589 0.9873 1.6977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531 
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05

A partir dos resultados, podemos ver que a estimativa do coeficiente para a variável preditora de horas mudou ligeiramente e o ajuste geral do modelo melhorou.

O modelo de mínimos quadrados ponderados tem um erro padrão residual de 1,199 , em comparação com 9,224 no modelo de regressão linear simples original.

Isto indica que os valores previstos produzidos pelo modelo de mínimos quadrados ponderados estão muito mais próximos das observações reais em comparação com os valores previstos produzidos pelo modelo de regressão linear simples.

O modelo de mínimos quadrados ponderados também tem um R-quadrado de 0,6762 , em comparação com 0,6296 no modelo de regressão linear simples original.

Isso indica que o modelo de mínimos quadrados ponderados é capaz de explicar mais a variância nas notas dos exames do que o modelo de regressão linear simples.

Estas medidas indicam que o modelo de mínimos quadrados ponderados proporciona um melhor ajuste aos dados em comparação com o modelo de regressão linear simples.

Recursos adicionais

Como realizar regressão linear simples em R
Como realizar regressão linear múltipla em R
Como realizar regressão quantílica em R