Como encontrar o modo de dados agrupados: com exemplos

Freqüentemente, queremos calcular a forma como os dados são agrupados de alguma forma.

Lembre-se que a moda representa o valor que aparece com mais frequência.

Por exemplo, suponha que temos os seguintes dados agrupados:

Embora não seja possível calcular a moda exata, pois não conhecemos os valores dos dados brutos , é possível estimar a moda usando a seguinte fórmula:

Modo de dados agrupados = L + W[(F _m – F ₁ )/( (F _m -F ₁ ) + (F _m – F ₂ ) )]

Ouro:

• L : Limite inferior da classe modal
• W : Largura da classe modal
• F _m : Frequência da classe modal
• F ₁ : Frequência do curso imediatamente anterior ao curso modal
• F ₂ : Frequência do curso imediatamente após o curso modal

Nota : A classe modal é simplesmente a classe com maior frequência. No exemplo acima, a classe modal seria 21-30, pois possui a frequência mais alta.

Os exemplos a seguir mostram como calcular a moda dos dados agrupados em diferentes cenários.

Exemplo 1: Calcule a moda dos dados agrupados

Suponha que temos a seguinte distribuição de frequência que mostra a nota do exame de 40 alunos de uma determinada turma:

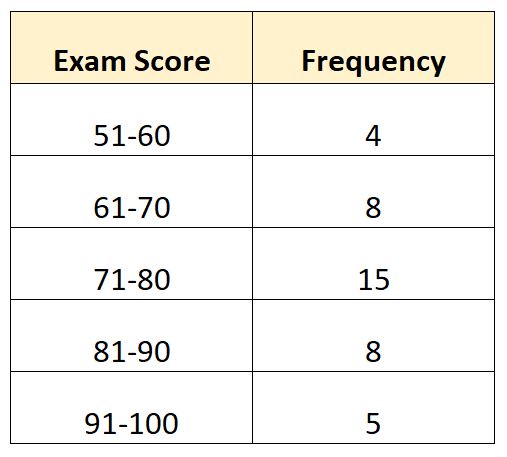
Neste exemplo, a classe modal é 71-80.

Sabendo disso, podemos calcular os seguintes valores:

• L : Limite inferior da classe modal: 71
• W : Largura da classe modal: 9
• F _m : Frequência da aula modal: 15
• F ₁ : Frequência do curso imediatamente anterior ao curso modal: 8
• F ₂ : Frequência do curso imediatamente após o curso modal: 8

Podemos inserir esses valores na fórmula para calcular o modo de distribuição:

• Modo = L + W[(F _m – F ₁ )/( (F _m -F ₁ ) + (F _m – F ₂ ) )]
• Modo = 71 + 9[(15-8) / ((15-8) + (15-8) )]
• Modo = 75,5

Estimamos que a pontuação do exame modal seja 75,5 .

Exemplo 2: Calcule o modo de dados agrupados

Suponha que temos a seguinte distribuição de frequência que mostra o número de pontos marcados por jogo por 60 jogadores de basquete:

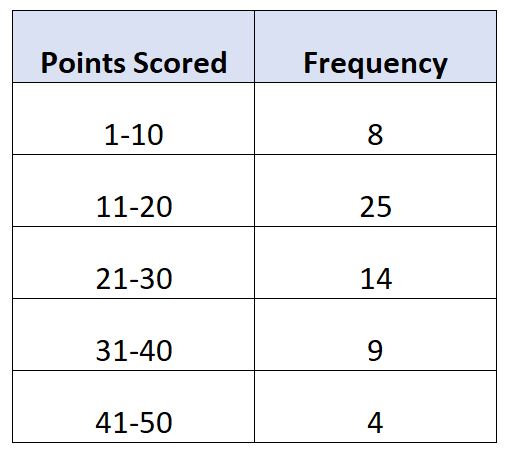
Neste exemplo, a classe modal é 11-20.

Sabendo disso, podemos calcular os seguintes valores:

• L : Limite inferior da classe modal: 11
• W : Largura da classe modal: 9
• F _m : Frequência da aula modal: 25
• F ₁ : Frequência do curso imediatamente anterior ao curso modal: 8
• F ₂ : Frequência do curso imediatamente após o curso modal: 14

Podemos inserir esses valores na fórmula para calcular o modo de distribuição:

• Modo = L + W[(F _m – F ₁ )/( (F _m -F ₁ ) + (F _m – F ₂ ) )]
• Modo = 11 + 9[(25-8) / ((25-8) + (25-14) )]
• Moda = 16,46

Estimamos que o número de pontos modais marcados seja 16,46 .

Recursos adicionais

Os tutoriais a seguir explicam como realizar outras operações comuns com dados agrupados:

Como encontrar a média e o desvio padrão de dados agrupados
Como encontrar a mediana de dados agrupados
Como calcular a classificação percentil para dados agrupados