O que é um nível beta em estatísticas? (definição e #038; exemplo)
Em estatística, usamos testes de hipóteses para determinar se uma hipótese sobre um parâmetro populacional é verdadeira.
Um teste de hipótese sempre tem as duas hipóteses a seguir:
Hipótese nula (H 0 ): Os dados amostrais são consistentes com a crença dominante em relação ao parâmetro populacional.
Hipótese Alternativa ( HA ): Os dados da amostra sugerem que a hipótese declarada na hipótese nula não é verdadeira. Em outras palavras, uma causa não aleatória influencia os dados.
Sempre que realizamos um teste de hipótese, há sempre quatro resultados possíveis:
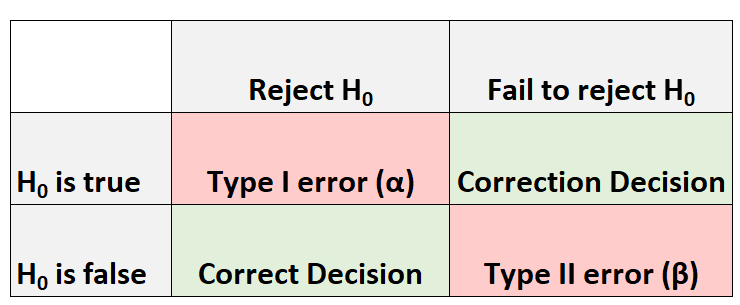
Existem dois tipos de erros que podemos cometer:
- Erro tipo I: rejeitamos a hipótese nula quando ela é realmente verdadeira. A probabilidade desse tipo de erro ser cometido é denotada por α .
- Erro tipo II: falhamos em rejeitar a hipótese nula quando ela é realmente falsa. A probabilidade deste tipo de erro ser cometido é anotada como β .
A relação entre alfa e beta
Idealmente, os pesquisadores desejam que a probabilidade de cometer um erro do Tipo I e a probabilidade de cometer um erro do Tipo II sejam baixas.
No entanto, existe um compromisso entre essas duas probabilidades. Se diminuirmos o nível alfa, poderemos diminuir a probabilidade de rejeitar uma hipótese nula quando esta for realmente verdadeira, mas isto na verdade aumenta o nível beta – a probabilidade de não conseguirmos rejeitar a hipótese nula quando esta está errada.
A relação entre poder e beta
O poder de um teste de hipótese refere-se à probabilidade de detectar um efeito ou diferença quando um efeito ou diferença está realmente presente. Em outras palavras, é a probabilidade de rejeitar corretamente uma hipótese nula falsa.
É calculado da seguinte forma:
Potência = 1 – β
Em geral, os pesquisadores desejam que o poder de um teste seja alto para que, caso haja algum efeito ou diferença, o teste seja capaz de detectá-lo.
Pela equação acima, podemos ver que a melhor forma de aumentar o poder de um teste é reduzir o nível beta. E a melhor maneira de reduzir o nível beta geralmente é aumentar o tamanho da amostra.
Os exemplos a seguir mostram como calcular o nível beta de um teste de hipótese e demonstram por que aumentar o tamanho da amostra pode reduzir o nível beta.
Exemplo 1: Calcular Beta para um Teste de Hipótese
Suponha que um pesquisador queira testar se o peso médio dos widgets produzidos em uma fábrica é inferior a 500 onças. Sabemos que o desvio padrão dos pesos é de 24 onças e o pesquisador decide coletar uma amostra aleatória de 40 widgets.
Realizará a seguinte hipótese em α = 0,05:
- H 0 : µ = 500
- HA : μ < 500
Agora imagine que o peso médio dos widgets produzidos seja, na verdade, 490 onças. Em outras palavras, a hipótese nula deve ser rejeitada.
Podemos usar as seguintes etapas para calcular o nível beta – a probabilidade de não rejeitar a hipótese nula quando ela de fato deveria ser rejeitada:
Etapa 1: Encontre a região sem rejeição.
De acordo com a calculadora do valor crítico Z, o valor crítico esquerdo em α = 0,05 é -1,645 .
Etapa 2: Encontre a amostra mínima que não conseguiremos rejeitar.
A estatística de teste é calculada como z = ( x – μ) / (s/ √n )
Então, podemos resolver esta equação para a média amostral:
- x = µ – z*(s/ √n )
- x = 500 – 1,645*(24/ √40 )
- x = 493,758
Etapa 3: Determine a probabilidade de que a média amostral mínima realmente ocorra.
Podemos calcular essa probabilidade da seguinte forma:
- P(Z ≥ (493,758 – 490) / (24/√ 40 ))
- P(Z ≥ 0,99)
De acordo com a calculadora CDF normal , a probabilidade de Z ≥ 0,99 é 0,1611 .
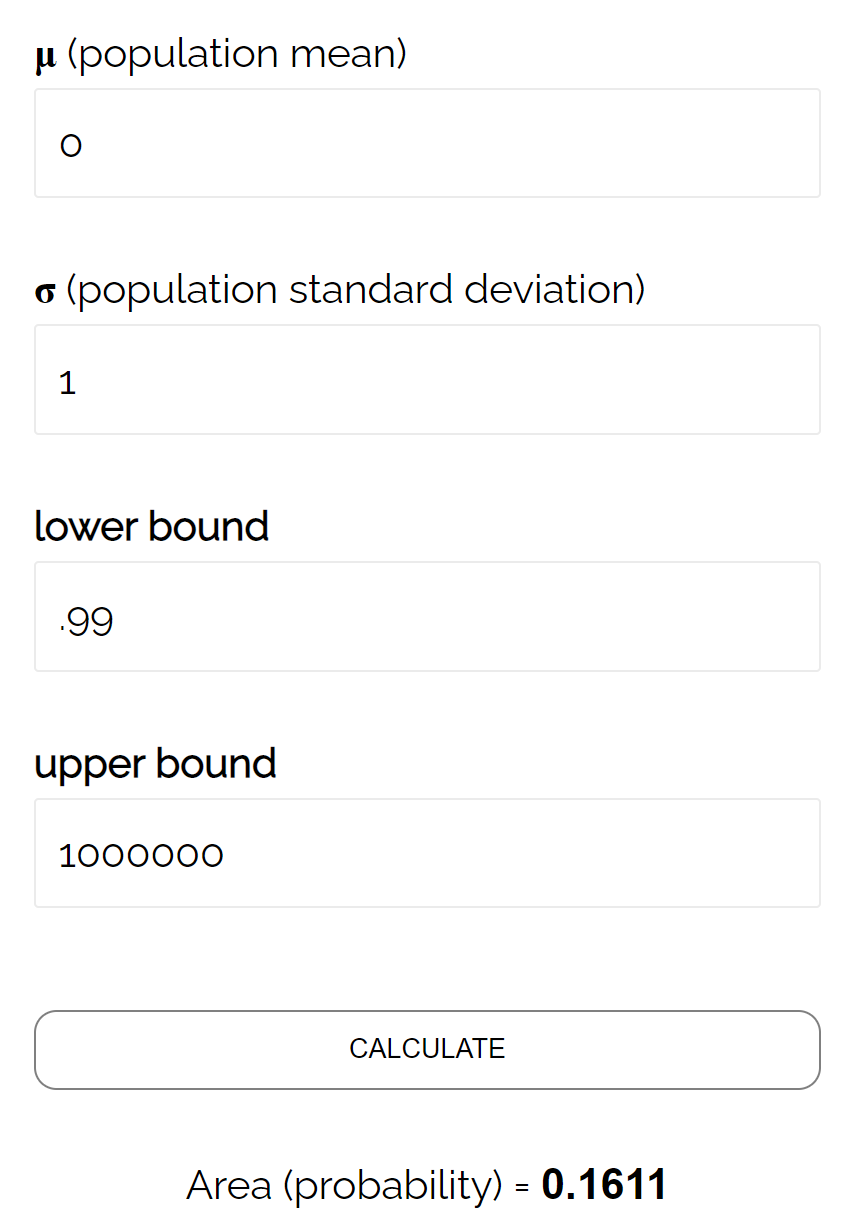
Assim, o nível beta para este teste é β = 0,1611. Isso significa que há 16,11% de chance de não detectar a diferença se a média real for 490 onças.
Exemplo 2: Calcular Beta para um teste com tamanho de amostra maior
Agora suponha que o pesquisador realize exatamente o mesmo teste de hipótese, mas em vez disso use uma amostra de n = 100 widgets. Podemos repetir as mesmas três etapas para calcular o nível beta deste teste:
Etapa 1: Encontre a região sem rejeição.
De acordo com a calculadora do valor crítico Z, o valor crítico esquerdo em α = 0,05 é -1,645 .
Etapa 2: Encontre a amostra mínima que não conseguiremos rejeitar.
A estatística de teste é calculada como z = ( x – μ) / (s/ √n )
Então, podemos resolver esta equação para a média amostral:
- x = µ – z*(s/ √n )
- x = 500 – 1,645*(24/√ 100 )
- x = 496,05
Etapa 3: Determine a probabilidade de que a média amostral mínima realmente ocorra.
Podemos calcular essa probabilidade da seguinte forma:
- P(Z ≥ (496,05 – 490) / (24/√ 100 ))
- P(Z ≥ 2,52)
De acordo com a calculadora CDF normal , a probabilidade de Z ≥ 2,52 é 0,0059.
Assim, o nível beta para este teste é β = 0,0059. Isso significa que há apenas 0,59% de chance de não detectar a diferença se a média real for 490 onças.
Observe que simplesmente aumentando o tamanho da amostra de 40 para 100, o pesquisador conseguiu reduzir o nível beta de 0,1611 para 0,0059.
Bônus: use esta calculadora de erro Tipo II para calcular automaticamente o nível beta de um teste.
Recursos adicionais
Introdução ao teste de hipóteses
Como escrever uma hipótese nula (5 exemplos)
Uma explicação dos valores P e significância estatística