A curtose pode ser negativa?

Nas estatísticas, a curtose é usada para descrever a forma de uma distribuição de probabilidade.

Especificamente, ele nos diz quão bem os valores dos dados se agrupam nas caudas ou no topo de uma distribuição.

A curtose de uma distribuição pode ser negativa, zero ou positiva.

Curtose Zero

Se uma distribuição tiver uma curtose de 0, então ela é igual à distribuição normal que tem o seguinte formato de sino:

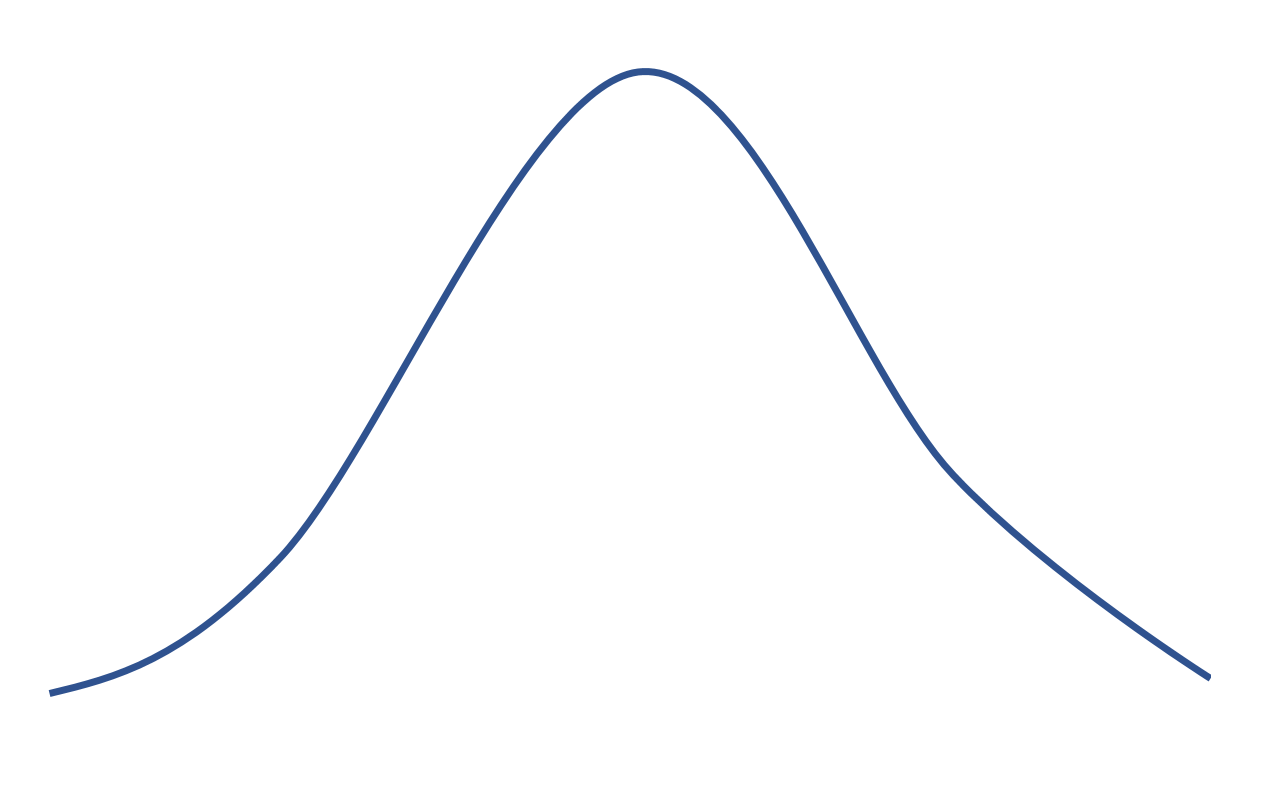
Curtose positiva

Se uma distribuição tiver curtose positiva, diz-se que é leptocúrtica , o que significa que tem um pico mais nítido e caudas mais pesadas em comparação com uma distribuição normal.

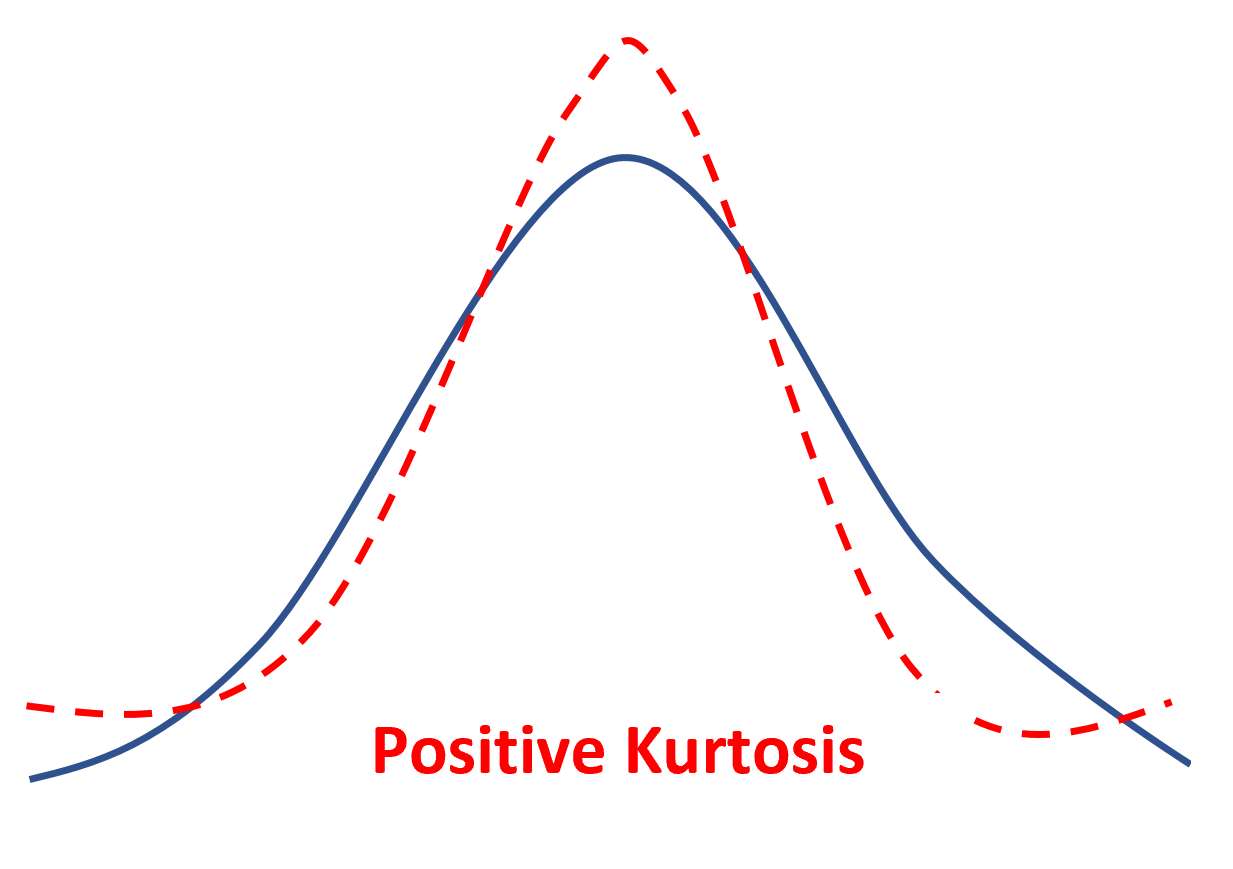
Isso significa simplesmente que menos valores de dados estão localizados perto da média e mais valores de dados estão localizados nas caudas.

A distribuição mais conhecida que apresenta curtose positiva é a distribuição t, que possui pico mais nítido e caudas mais pesadas em comparação à distribuição normal.

Curtose negativa

Se uma distribuição tiver curtose negativa, ela é considerada platicúrtica , o que significa que tem um pico mais achatado e caudas mais finas em comparação com uma distribuição normal.

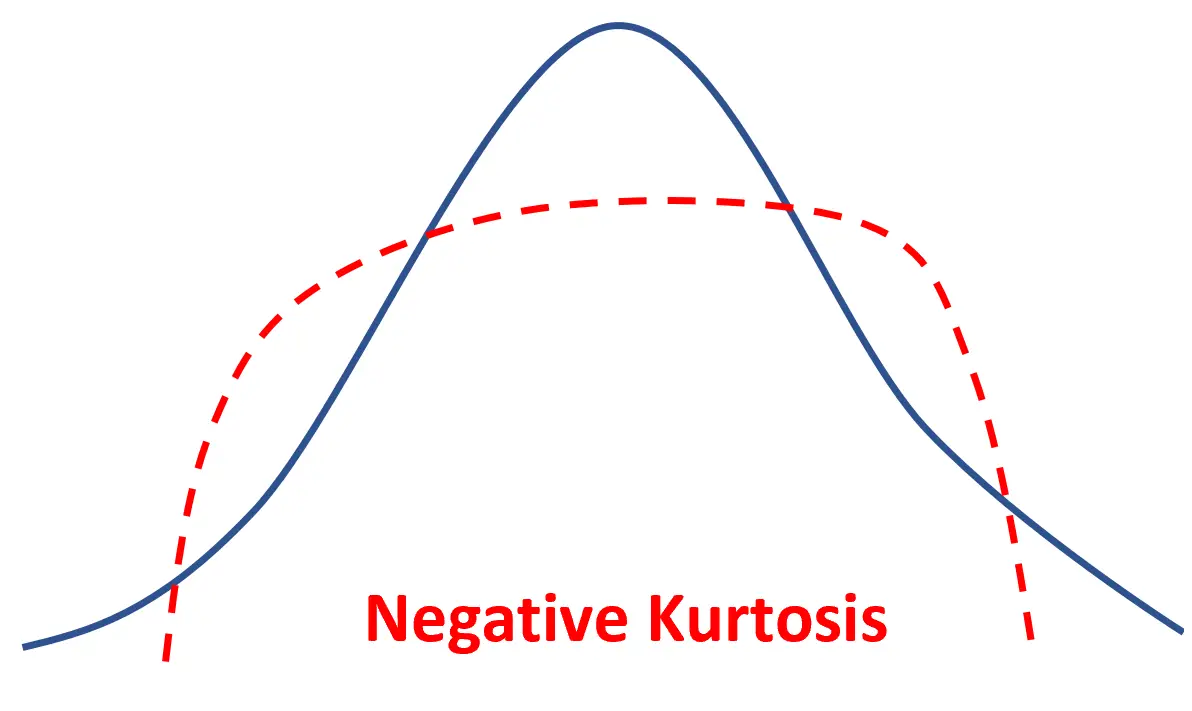
Isso significa simplesmente que mais valores de dados estão localizados perto da média e menos valores de dados estão localizados nas caudas.

Um exemplo extremo de distribuição que apresenta curtose negativa é a distribuição uniforme , que não tem picos e é uma distribuição completamente plana.

Quando usar lisonjeiro na prática

Na prática, muitas vezes medimos a curtose de uma distribuição na fase exploratória da análise, quando estamos simplesmente tentando compreender melhor os dados.

Portanto, se observarmos que a curtose é positiva, sabemos que estamos trabalhando com uma distribuição que possui menos valores de dados localizados próximos ao centro e mais valores de dados distribuídos ao longo das caudas.

Por outro lado, se observarmos que a curtose é negativa, sabemos que estamos trabalhando com uma distribuição que possui mais valores de dados localizados próximos ao centro e menos valores de dados nas caudas.

Recursos adicionais

Para encontrar a assimetria e a curtose de uma determinada distribuição, você pode inserir os valores dos dados brutos nesta calculadora de assimetria e curtose , que informará a assimetria e a curtose da distribuição.

Um dos testes estatísticos mais populares usados para determinar se uma determinada distribuição apresenta ou não assimetria e curtose que corresponde a uma distribuição normal é o teste de Jarque Bera .

A Khan Academy também tem uma bela série de vídeos que descrevem como classificar formas de distribuição.