Como realizar a regressão ols em python (com exemplo)
A regressão de mínimos quadrados ordinários (OLS) é um método que nos permite encontrar uma linha que melhor descreve a relação entre uma ou mais variáveis preditoras e uma variável de resposta .
Este método nos permite encontrar a seguinte equação:
ŷ=b 0 + b 1 x
Ouro:
- ŷ : O valor estimado da resposta
- b 0 : A origem da linha de regressão
- b 1 : A inclinação da linha de regressão
Esta equação pode nos ajudar a compreender a relação entre o preditor e a variável de resposta e pode ser usada para prever o valor de uma variável de resposta dado o valor da variável preditora.
O exemplo passo a passo a seguir mostra como realizar a regressão OLS em Python.
Etapa 1: crie os dados
Para este exemplo, criaremos um conjunto de dados contendo as duas variáveis a seguir para 15 alunos:
- Número total de horas estudadas
- Resultado de exame
Realizaremos uma regressão OLS, usando horas como variável preditora e pontuação no exame como variável resposta.
O código a seguir mostra como criar esse conjunto de dados falso em pandas:
import pandas as pd #createDataFrame df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14], ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]}) #view DataFrame print (df) hours score 0 1 64 1 2 66 2 4 76 3 5 73 4 5 74 5 6 81 6 6 83 7 7 82 8 8 80 9 10 88 10 11 84 11 11 82 12 12 91 13 12 93 14 14 89
Etapa 2: realizar uma regressão OLS
A seguir, podemos usar as funções do módulo statsmodels para realizar uma regressão OLS, usando horas como variável preditora e pontuação como variável de resposta :
import statsmodels.api as sm
#define predictor and response variables
y = df[' score ']
x = df[' hours ']
#add constant to predictor variables
x = sm. add_constant (x)
#fit linear regression model
model = sm. OLS (y,x). fit ()
#view model summary
print ( model.summary ())
OLS Regression Results
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1
Covariance Type: non-robust
==================================================== ============================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================
Na coluna coef , podemos ver os coeficientes de regressão e escrever a seguinte equação de regressão ajustada:
Pontuação = 65,334 + 1,9824*(horas)
Isso significa que cada hora adicional estudada está associada a um aumento médio na pontuação do exame de 1,9824 pontos.
O valor original de 65.334 nos indica a nota média esperada no exame para um aluno que estuda zero horas.
Também podemos usar essa equação para encontrar a pontuação esperada no exame com base no número de horas que um aluno estuda.
Por exemplo, um aluno que estuda 10 horas deverá obter nota 85.158 no exame:
Pontuação = 65,334 + 1,9824*(10) = 85,158
Veja como interpretar o restante do resumo do modelo:
- P(>|t|): Este é o valor p associado aos coeficientes do modelo. Como o valor p para horas (0,000) é inferior a 0,05, podemos afirmar que existe uma associação estatisticamente significativa entre horas e pontuação .
- R-quadrado: Isso nos diz que o percentual de variação nas notas dos exames pode ser explicado pelo número de horas estudadas. Nesse caso, 83,1% da variação nas notas pode ser explicada pelas horas estudadas.
- Estatística F e valor p: A estatística F ( 63,91 ) e o valor p correspondente ( 2,25e-06 ) nos dizem a significância geral do modelo de regressão, ou seja, se as variáveis preditoras no modelo são úteis para explicar a variação. na variável de resposta. Como o valor p neste exemplo é inferior a 0,05, nosso modelo é estatisticamente significativo e as horas são consideradas úteis para explicar a variação da pontuação .
Etapa 3: visualize a linha de melhor ajuste
Finalmente, podemos usar o pacote de visualização de dados matplotlib para visualizar a linha de regressão ajustada aos pontos de dados reais:
import matplotlib. pyplot as plt
#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )
#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')
#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)
#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )
#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')
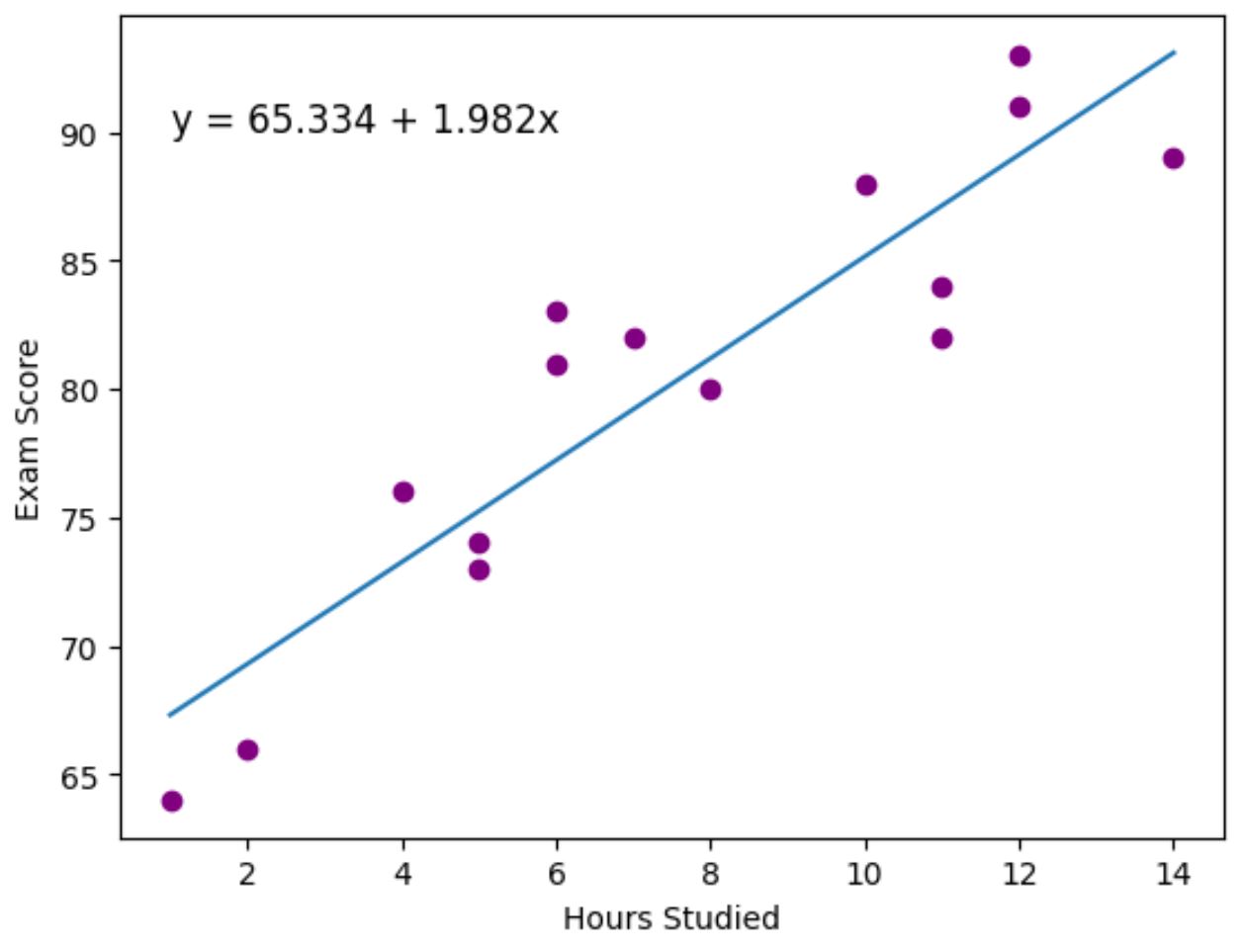
Os pontos roxos representam os pontos de dados reais e a linha azul representa a linha de regressão ajustada.
Também usamos a função plt.text() para adicionar a equação de regressão ajustada ao canto superior esquerdo do gráfico.
Olhando para o gráfico, parece que a linha de regressão ajustada captura muito bem a relação entre a variável horas e a variável pontuação .
Recursos adicionais
Os tutoriais a seguir explicam como realizar outras tarefas comuns em Python:
Como realizar regressão logística em Python
Como realizar regressão exponencial em Python
Como calcular AIC de modelos de regressão em Python