Operações em conjuntos: união, intersecção, complemento e diferença

Um conjunto é uma coleção de elementos.

Designamos um conjunto com letra maiúscula e definimos os elementos do conjunto usando chaves. Por exemplo, suponha que temos um conjunto chamado “A” com os elementos 1, 2, 3. Escreveríamos isso da seguinte forma:

UMA = {1, 2, 3}

Este tutorial explica as operações de conjunto mais comumente usadas em probabilidade e estatística.

União

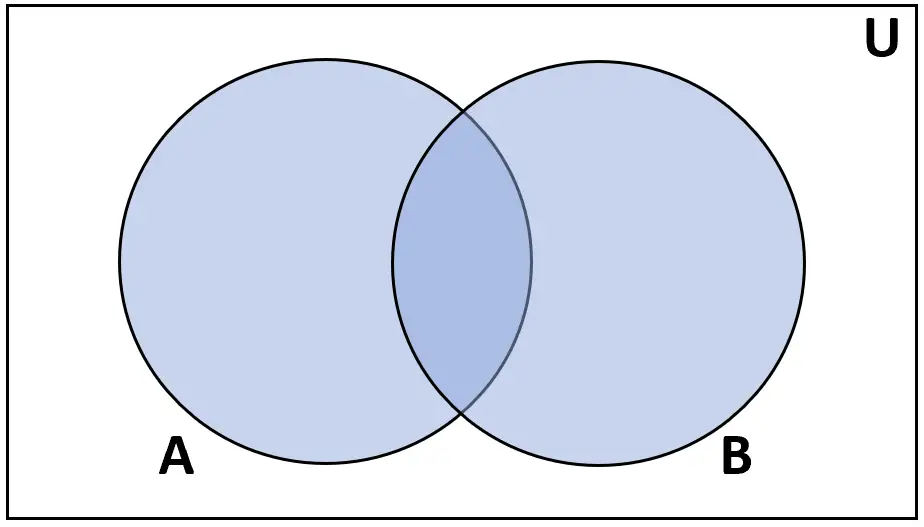
Definição: A união dos conjuntos A e B é o conjunto de elementos encontrados em A ou em B.

Classificação: A ∪ B

Exemplos:

• {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
• {1, 2} ∪ {1, 2} = {1, 2}
• {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}

Interseção

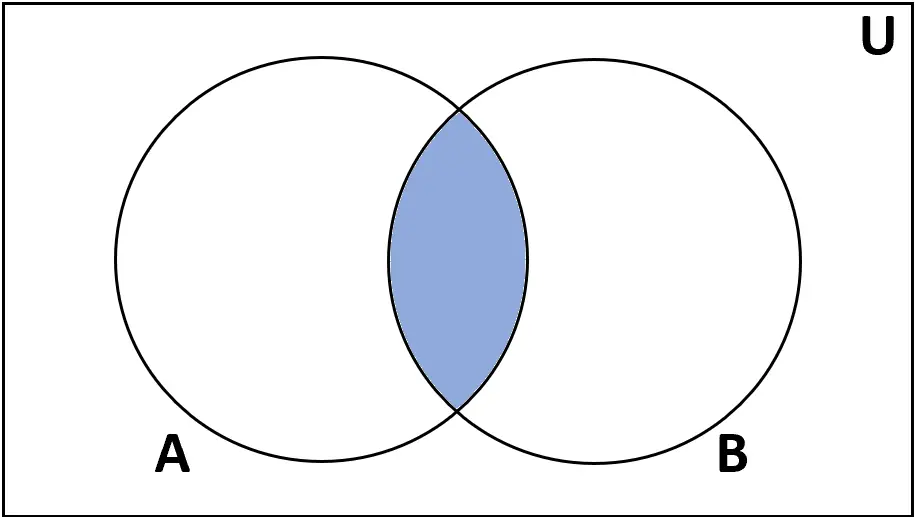
Definição: A interseção dos conjuntos A e B é o conjunto de elementos encontrados em A e B.

Notação: A ∩ B

Exemplos:

• {1, 2, 3} ∩ {4, 5, 6} = {∅}
• {1, 2} ∩ {1, 2} = {1, 2}
• {1, 2, 3} ∩ {3, 4} = {3}

Complemento

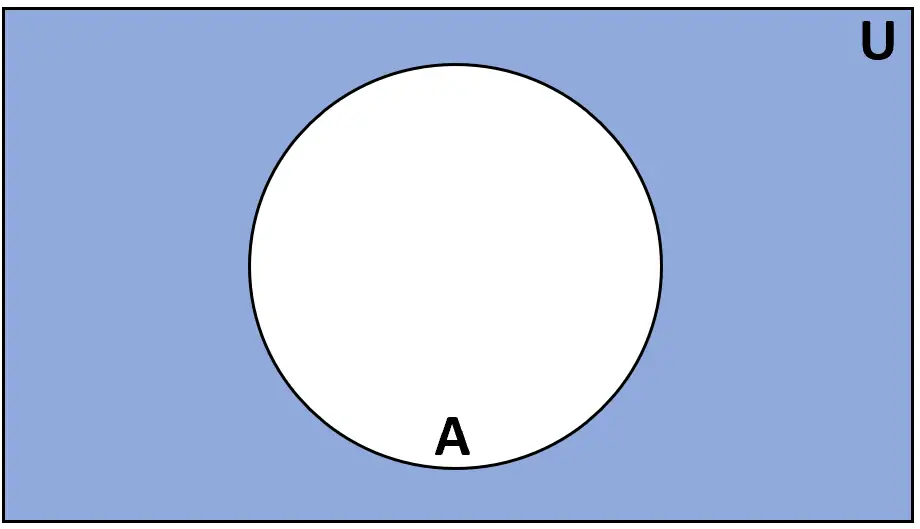
Definição: O complemento do conjunto A é o conjunto de elementos que estão no conjunto universal U, mas não estão em A.

Classificação: A’ ou ^Ac

Exemplos:

• Se U = {1, 2, 3, 4, 5, 6} e A = {1, 2}, então A ^c = {3, 4, 5, 6}
• Se U = {1, 2, 3} e A = {1, 2}, então A ^c = {3}

Diferença

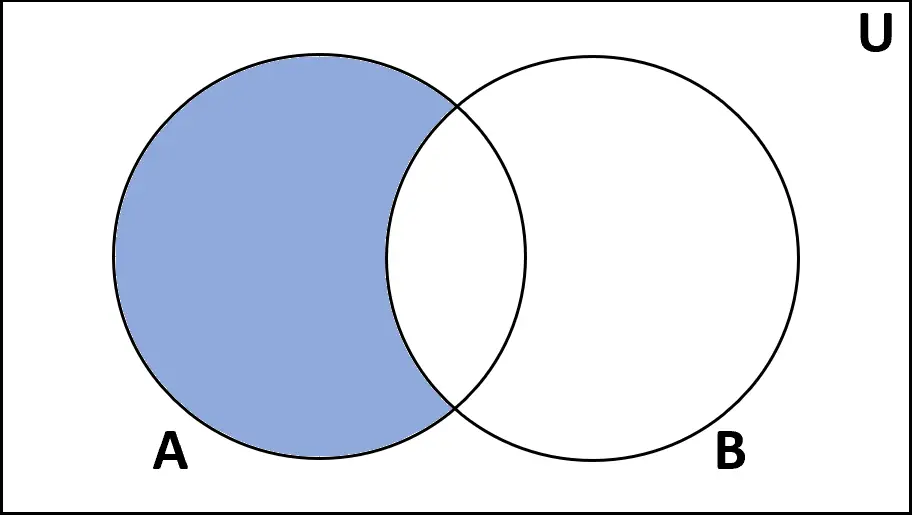
Definição: A diferença entre os conjuntos A e B é o conjunto de elementos encontrados em A, mas não em B.

Avaliações: A – B

Exemplos:

• {1, 2, 3} – {2, 3, 4} = {1}
• {1, 2} – {1, 2} = {∅}
• {1, 2, 3} – {4, 5} = {1, 2, 3}

Diferença simétrica

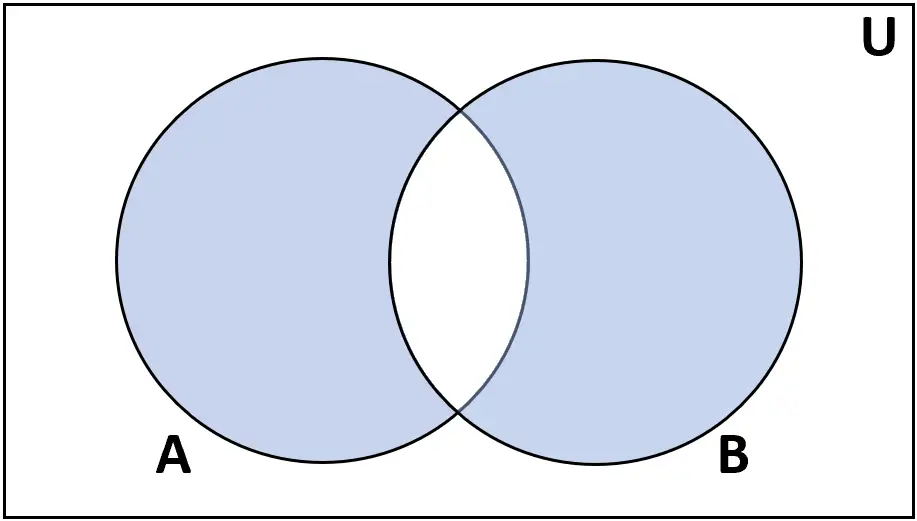
Definição: A diferença simétrica dos conjuntos A e B é o conjunto de elementos encontrados em A ou B, mas não em ambos.

Classificação: AΔB

Exemplos:

• {1, 2, 3} Δ {2, 3, 4} = {1, 4}
• {1, 2} Δ {1, 2} = {∅}
• {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}

produto cartesiano

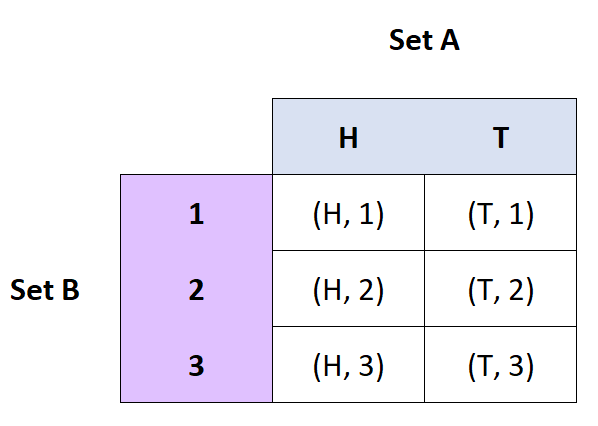
Definição: O produto cartesiano dos conjuntos A e B é o conjunto dos pares ordenados de A e B.

Classificação: A x B

Exemplos:

• Se A = {H, T} e B = {1, 2, 3}, então A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( T, 2), (T, 3)}
• Se A = {T, H} e B = {1, 2, 3}, então A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( H, 2), (H, 3)}