Padronização ou normalização: qual a diferença?

Padronização e normalização são duas maneiras de redimensionar dados.

A normalização dimensiona um conjunto de dados para ter uma média de 0 e um desvio padrão de 1. Para fazer isso, ela usa a seguinte fórmula:

x _novo = (x _i – x ) / s

Ouro:

• x _i : o i- ^ésimo valor do conjunto de dados
• x : A amostra significa
• s : o desvio padrão da amostra

A normalização redimensiona um conjunto de dados para que cada valor fique entre 0 e 1. Isso é feito usando a seguinte fórmula:

x _novo = (x _i – x _min ) / (x _máx – x _min )

Ouro:

• x _i : o i- ^ésimo valor do conjunto de dados
• x _min : o valor mínimo no conjunto de dados
• x _max : o valor máximo no conjunto de dados

Os exemplos a seguir mostram como padronizar e normalizar um conjunto de dados na prática.

Exemplo: Como padronizar dados

Suponha que temos o seguinte conjunto de dados:

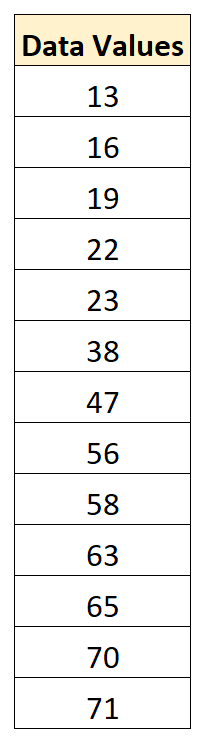
O valor médio no conjunto de dados é 43,15 e o desvio padrão é 22,13.

Para normalizar o primeiro valor de 13 , aplicaríamos a fórmula compartilhada anteriormente:

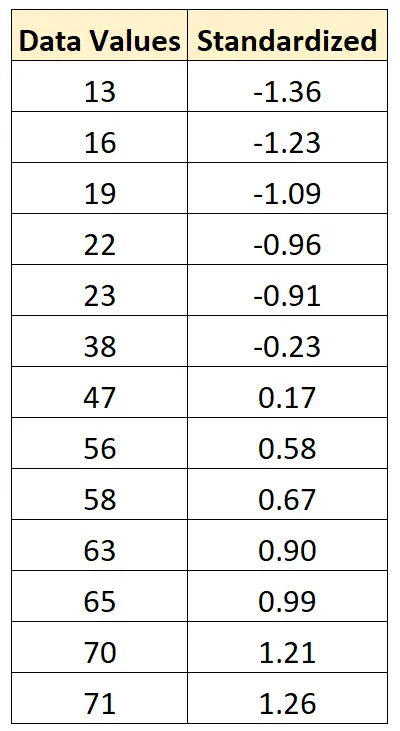
• x _novo = ( _xi – x ) / s = (13 – 43,15) / 22,13 = -1,36

Para normalizar o segundo valor de 16 , usaríamos a mesma fórmula:

• x _novo = ( _xi – x ) / s = (16 – 43,15) / 22,13 = -1,23

Para normalizar o terceiro valor de 19 , usaríamos a mesma fórmula:

• x _novo = ( _xi – x ) / s = (19 – 43,15) / 22,13 = -1,09

Podemos usar exatamente esta mesma fórmula para padronizar cada valor no conjunto de dados original:

Exemplo: como normalizar dados

Novamente, suponha que temos o seguinte conjunto de dados:

O valor mínimo no conjunto de dados é 13 e o valor máximo é 71.

Para normalizar o primeiro valor de 13 , aplicaríamos a fórmula compartilhada anteriormente:

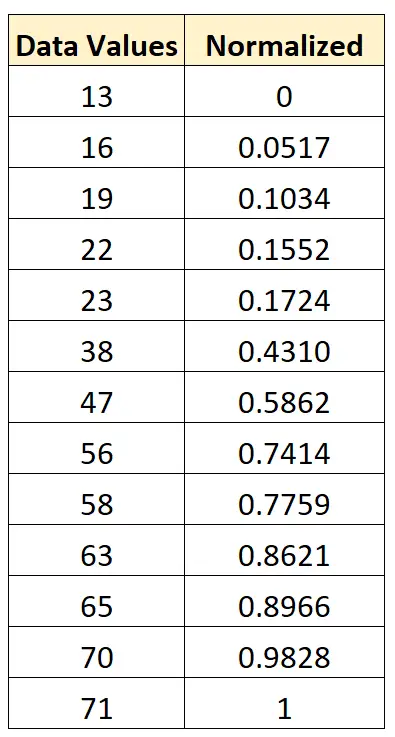
• x _novo = ( _xi – x _min ) / (x _máx – x _min ) = (13 – 13) / (71 – 13) = 0

Para normalizar o segundo valor de 16 , usaríamos a mesma fórmula:

• x _novo = ( _xi – x _min ) / (x _máx – x _min ) = (16 – 13) / (71 – 13) = 0,0517

Para normalizar o terceiro valor de 19 , usaríamos a mesma fórmula:

• x _novo = ( _xi – x _min ) / (x _máx – x _min ) = (19 – 13) / (71 – 13) = 0,1034

Podemos usar exatamente esta mesma fórmula para normalizar cada valor no conjunto de dados original entre 0 e 1:

Padronização ou normalização: quando utilizá-las?

Normalmente, normalizamos os dados quando estamos fazendo algum tipo de análise em que temos múltiplas variáveis medidas em escalas diferentes e queremos que cada uma das variáveis tenha o mesmo intervalo.

Isto evita que uma variável tenha influência indevida, especialmente se for medida em unidades diferentes (ou seja, se uma variável for medida em polegadas e outra em jardas).

Por outro lado, normalmente normalizamos os dados quando queremos saber quantos desvios padrão cada valor em um conjunto de dados está em relação à média.

Por exemplo, podemos ter uma lista de notas de exames para 500 alunos de uma determinada escola e gostaríamos de saber quantos desvios padrão cada nota de exame está em relação à nota média.

Nesse caso, poderíamos normalizar os dados brutos para conhecer essas informações. Então, uma pontuação padronizada de 1,26 nos diria que a pontuação do exame desse aluno em particular está 1,26 desvios-padrão acima da pontuação média do exame.

Quer você decida normalizar ou padronizar seus dados, tenha em mente os seguintes pontos:

• Um conjunto de dados normalizado sempre terá valores entre 0 e 1.
• Um conjunto de dados padronizado terá média 0 e desvio padrão 1, mas não há limite superior ou inferior específico para os valores máximo e mínimo.

Dependendo do seu cenário específico, pode fazer mais sentido normalizar ou padronizar os dados.

Recursos adicionais

Os tutoriais a seguir explicam como padronizar e normalizar dados em diferentes softwares estatísticos:

Como normalizar dados em R
Como normalizar dados no Excel
Como normalizar dados em Python
Como padronizar dados em R