Um guia completo: o planejamento fatorial 2×2

Um planejamento fatorial 2 × 2 é um tipo de planejamento experimental que permite aos pesquisadores compreender os efeitos de duas variáveis independentes (cada uma com dois níveis ) em uma única variável dependente.

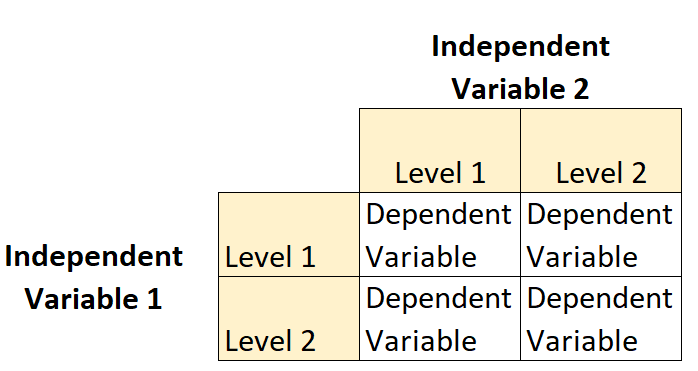
Por exemplo, suponha que um botânico queira compreender os efeitos da luz solar (baixa ou alta) e da frequência de rega (diária ou semanal) no crescimento de uma determinada espécie de planta.

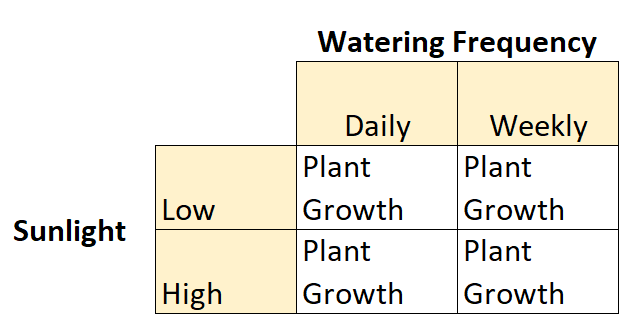
Este é um exemplo de experimento fatorial 2×2 porque existem duas variáveis independentes, cada uma com dois níveis:

• Variável independente nº 1: luz solar
  • Níveis: baixo, alto
• Variável independente #2: Frequência de rega
  • Níveis: diário, semanal

E há uma variável dependente: o crescimento das plantas.

O objetivo de um experimento fatorial 2 × 2

Um planejamento fatorial 2×2 permite analisar os seguintes efeitos:

Efeitos principais: São os efeitos que uma única variável independente tem sobre a variável dependente.

Por exemplo, no nosso cenário anterior, poderíamos analisar os seguintes efeitos principais:

• Principal efeito da luz solar no crescimento das plantas.
  • Podemos encontrar o crescimento médio de todas as plantas que receberam pouca luz solar.
  • Podemos encontrar o crescimento médio de todas as plantas que receberam muita luz solar.
• Principal efeito da frequência de rega no crescimento das plantas.
  • Podemos encontrar o crescimento médio de todas as plantas regadas diariamente.
  • Podemos encontrar o crescimento médio de todas as plantas regadas semanalmente.

Efeitos de interação: Ocorrem quando o efeito de uma variável independente sobre a variável dependente depende do nível da outra variável independente.

Por exemplo, no nosso cenário anterior, poderíamos analisar os seguintes efeitos de interação:

• O efeito da luz solar no crescimento das plantas depende da frequência de rega?
• O efeito da frequência de rega no crescimento das plantas depende da luz solar?

Visualize os principais efeitos e efeitos de interação

Quando usamos um planejamento fatorial 2 × 2, frequentemente representamos graficamente as médias para entender melhor os efeitos que as variáveis independentes têm sobre a variável dependente.

Por exemplo, considere o seguinte gráfico:

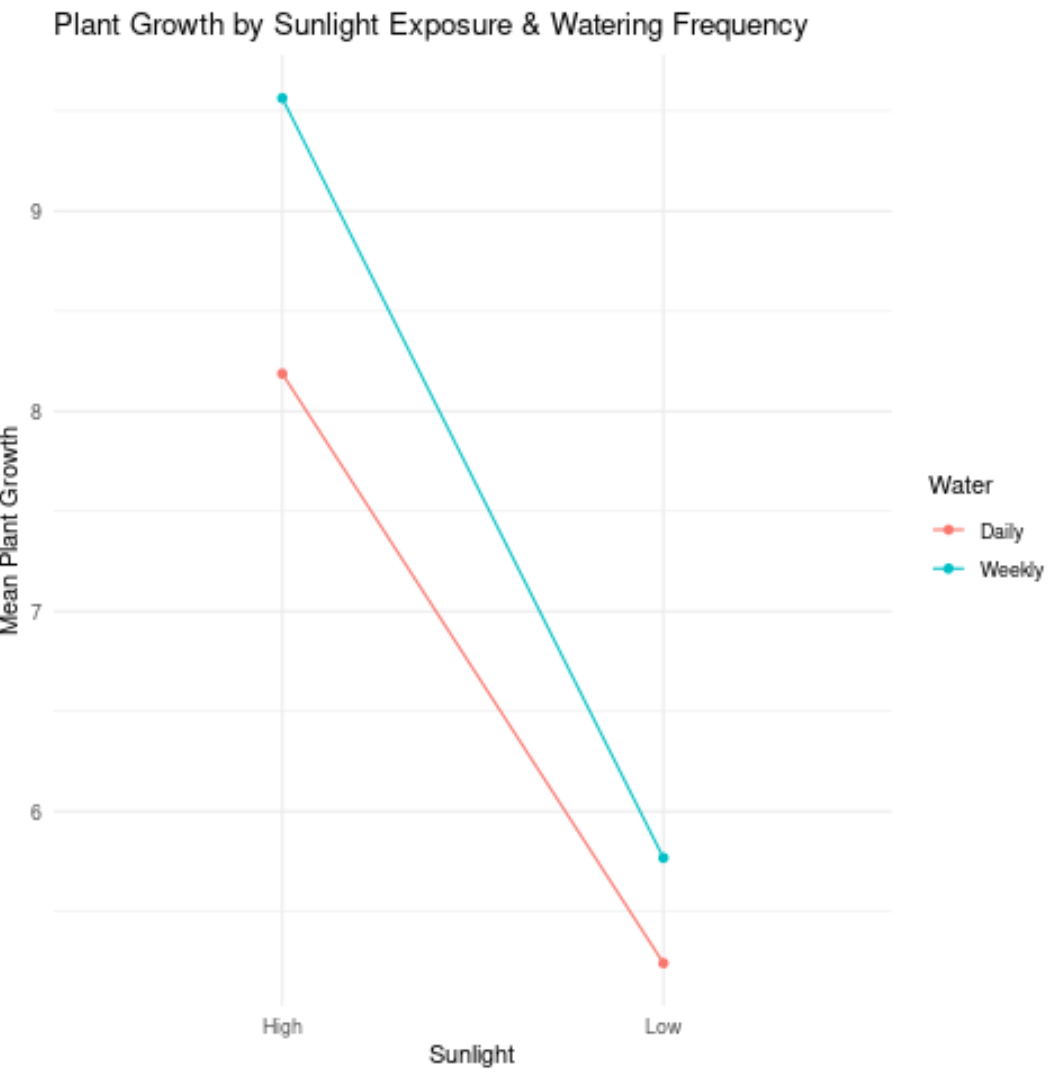
Veja como interpretar os valores no gráfico:

• O crescimento médio das plantas que receberam luz solar intensa e rega diária foi de cerca de 20 centímetros.
• O crescimento médio das plantas que receberam muita luz solar e rega semanal foi de cerca de 9,6 polegadas.
• O crescimento médio das plantas que receberam pouco sol e rega diária foi de cerca de 5,3 polegadas.
• O crescimento médio das plantas que receberam pouco sol e rega semanal foi de cerca de 5,8 polegadas.

Para determinar se existe efeito de interação entre as duas variáveis independentes, basta verificar se as linhas são paralelas ou não:

• Se as duas linhas do gráfico forem paralelas, não há efeito de interação.
• Se as duas linhas do gráfico não forem paralelas, há um efeito de interação.

No gráfico anterior, as duas linhas eram aproximadamente paralelas, portanto provavelmente não há efeito de interação entre a frequência de rega e a exposição solar.

No entanto, considere o seguinte gráfico:

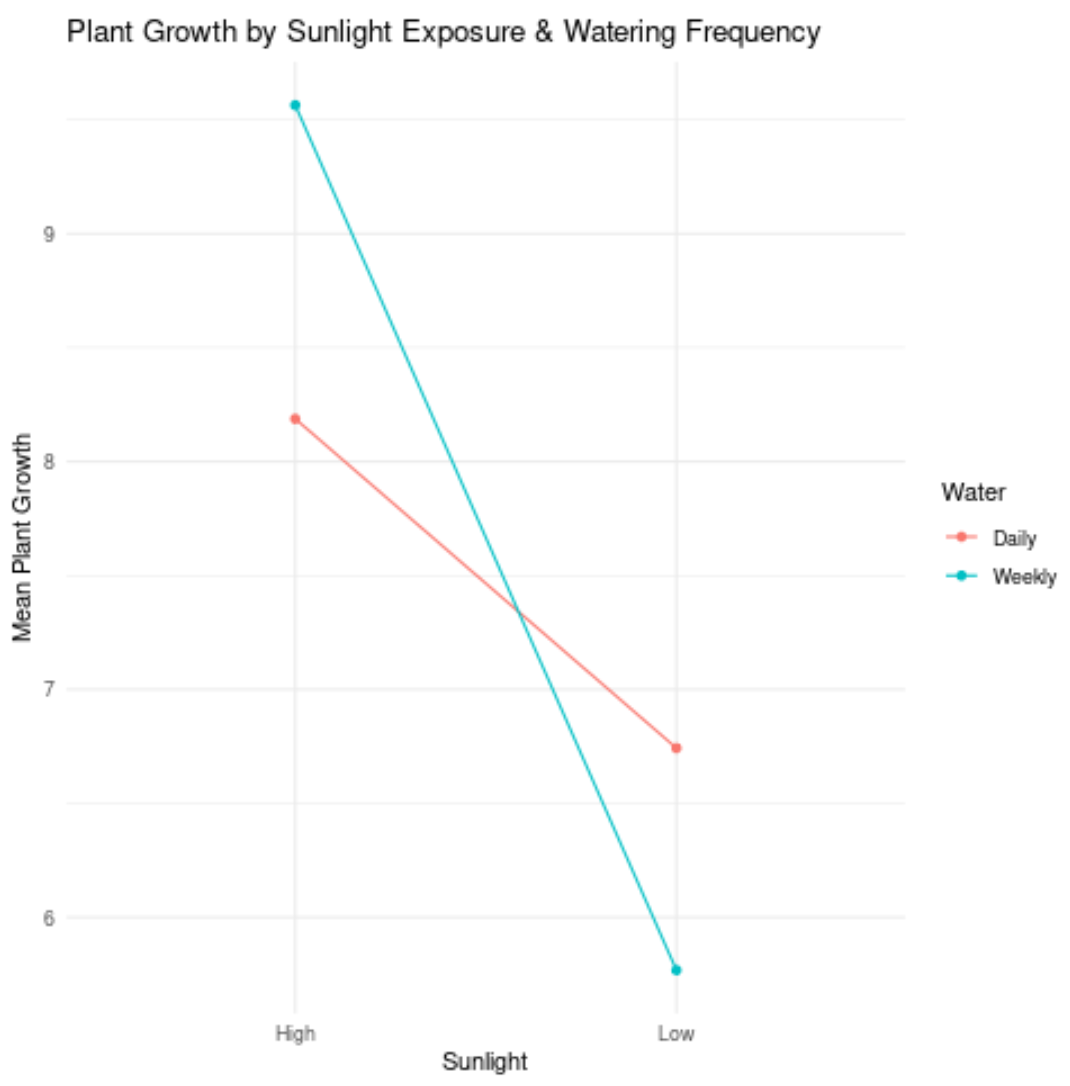
As duas linhas não são paralelas (na verdade, elas se cruzam!), o que indica que provavelmente existe um efeito de interação entre elas.

Por exemplo, isto significa que o efeito da luz solar no crescimento das plantas depende da frequência da rega.

Em outras palavras, a luz solar e a frequência de rega não afetam de forma independente o crescimento das plantas. Pelo contrário, existe um efeito de interação entre as duas variáveis independentes.

Como analisar um experimento fatorial 2×2

Traçar médias é uma forma visual de inspecionar os efeitos que as variáveis independentes têm sobre a variável dependente.

No entanto, também podemos realizar uma ANOVA bidirecional para testar formalmente se as variáveis independentes têm ou não uma relação estatisticamente significativa com a variável dependente.

Por exemplo, o código a seguir mostra como realizar uma ANOVA bidirecional para nosso cenário hipotético de fábrica em R:

 #make this example reproducible
set. seeds (0)

df <- data. frame (sunlight = rep(c(' Low ', ' High '), each = 30 ),
                 water = rep(c(' Daily ', ' Weekly '), each = 15 , times = 2 ),
                 growth = c(rnorm(15, 6, 2), rnorm(15, 7, 3), rnorm(15, 7, 2),
                                   rnorm(15, 10, 3)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

               Df Sum Sq Mean Sq F value Pr(>F)   
sunlight 1 52.5 52.48 8.440 0.00525 **
water 1 31.6 31.59 5.081 0.02813 * 
sunlight:water 1 12.8 12.85 2.066 0.15620   
Residuals 56 348.2 6.22                   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Veja como interpretar o resultado da ANOVA:

• O valor p associado à luz solar é 0,005 . Como esse número é inferior a 0,05, significa que a exposição à luz solar tem um efeito estatisticamente significativo no crescimento das plantas.
• O valor p associado à água é 0,028 . Como este valor é inferior a 0,05, significa que a frequência de rega também tem um efeito estatisticamente significativo no crescimento das plantas.
• O valor p para a interação entre luz solar e água é 0,156 . Como este valor não é inferior a 0,05, significa que não há efeito de interação entre a luz solar e a água.

Recursos adicionais

Um guia completo: o planejamento fatorial 2 × 3
Quais são os níveis de uma variável independente?
Variáveis independentes ou dependentes
O que é uma ANOVA fatorial?