Como realizar regressão linear no planilhas google

A regressão linear é um método que pode ser usado para quantificar a relação entre uma ou mais variáveis explicativas e uma variável de resposta .

Utilizamos regressão linear simples quando há apenas uma variável explicativa e regressão linear múltipla quando há duas ou mais variáveis explicativas.

Ambos os tipos de regressões podem ser realizados usando a função PROJ.LIN() do Planilhas Google, que usa a seguinte sintaxe:

PROJ.LIN (dados_conhecidos_y, dados_conhecidos_x, calcular_b, detalhado)

Ouro:

• dados_conhecidos_y: matriz de valores de resposta
• dados_conhecidos_x: Tabela de valores explicativos
• calcular_b: indica se deve ou não calcular o intercepto. Isso é VERDADEIRO por padrão e deixamos assim para regressão linear.
• detalhado: indica se devem ou não fornecer estatísticas de regressão adicionais além da inclinação e da interceptação. Isso é FALSO por padrão, mas especificaremos que é VERDADEIRO em nossos exemplos.

Os exemplos a seguir mostram como usar esta função na prática.

Regressão linear simples no Planilhas Google

Suponha que queiramos entender a relação entre as horas estudadas e os resultados dos exames. estudando para um exame e a nota obtida no exame.

Para explorar essa relação, podemos realizar uma regressão linear simples usando horas estudadas como variável explicativa e notas em exames como variável resposta.

A captura de tela a seguir mostra como realizar uma regressão linear simples usando um conjunto de dados de 20 alunos com a seguinte fórmula usada na célula D2:

= LINHA ( B2:B21 , A2:A21 , VERDADEIRO , VERDADEIRO )

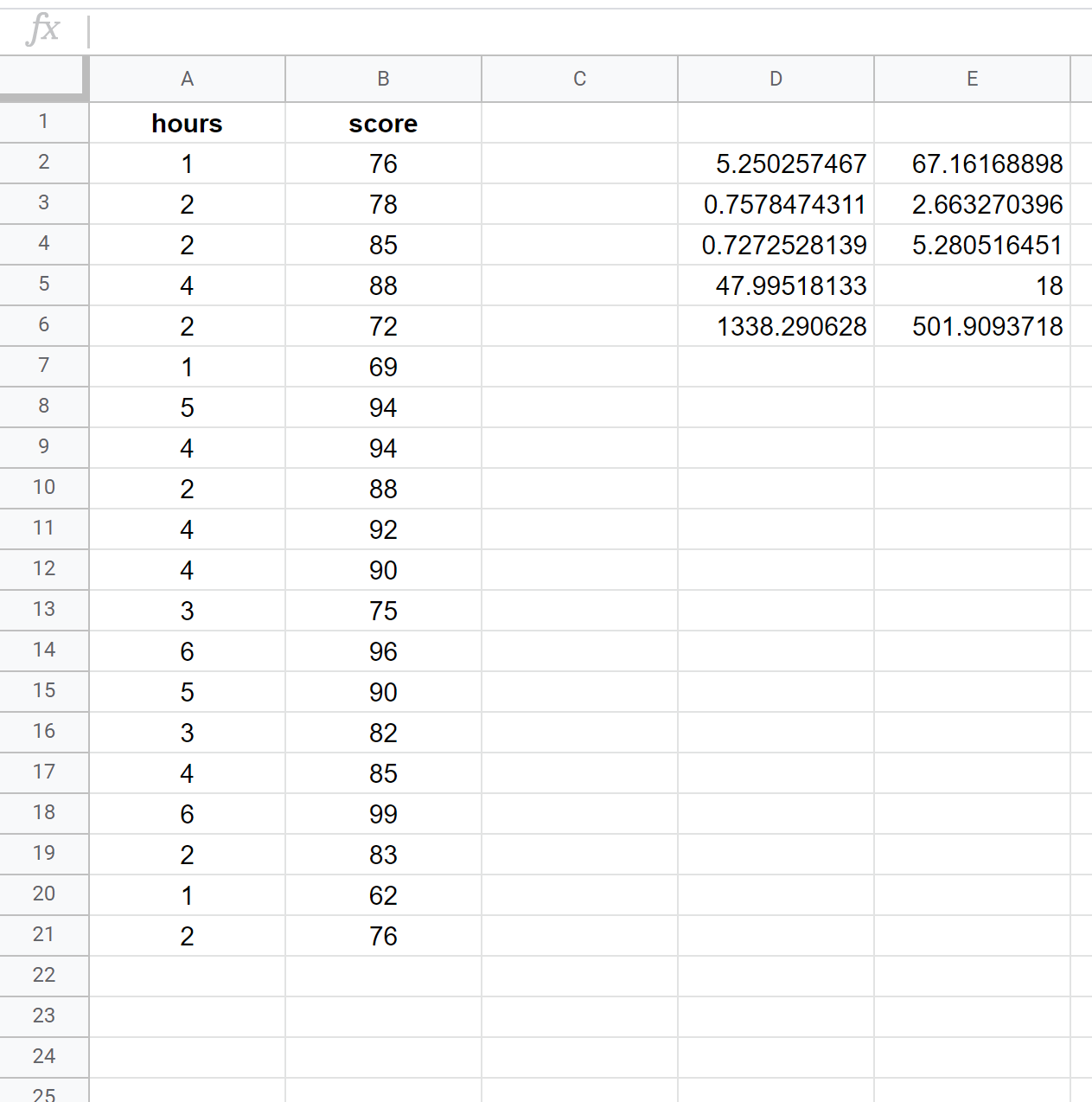
A captura de tela a seguir fornece anotações para a saída:

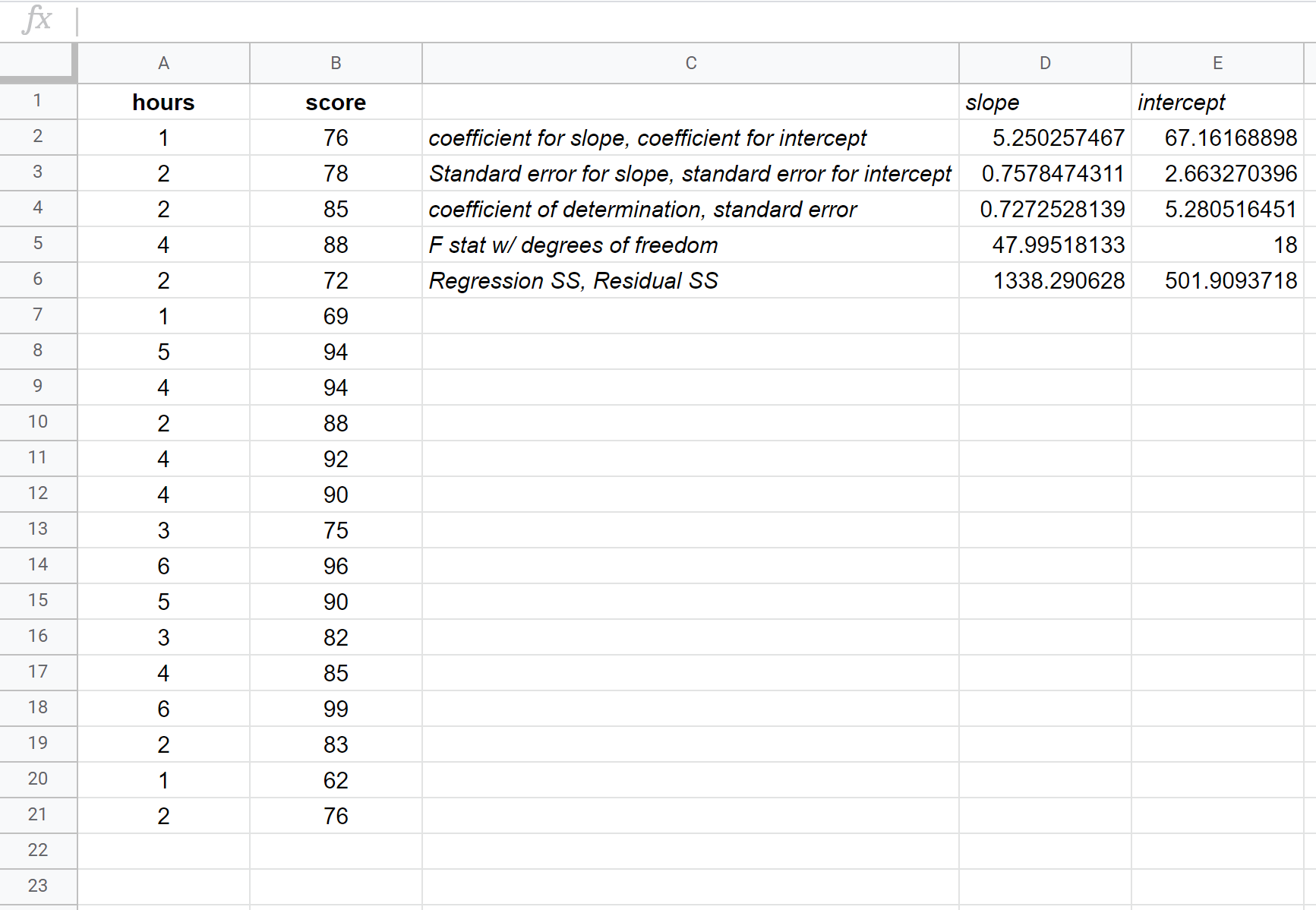
Veja como interpretar os números mais relevantes no resultado:

R Quadrado: 0,72725 . Isso é chamado de coeficiente de determinação. É a proporção da variância na variável resposta que pode ser explicada pela variável explicativa. Neste exemplo, aproximadamente 72,73% da variação nas notas dos exames pode ser explicada pela quantidade de horas estudadas.

Erro padrão: 5,2805 . Esta é a distância média entre os valores observados e a linha de regressão. Neste exemplo, os valores observados desviam-se em média 5,2805 unidades da linha de regressão.

Coeficientes: Os coeficientes nos fornecem os números necessários para escrever a equação de regressão estimada. Neste exemplo, a equação de regressão estimada é:

Nota do exame = 67,16 + 5,2503*(horas)

Interpretamos o coeficiente de horas como significando que para cada hora adicional estudada, a nota do exame deve aumentar em média 5,2503 . Interpretamos o coeficiente da interceptação como significando que a nota esperada no exame para um aluno que estuda zero horas é 67,16 .

Podemos usar esta equação de regressão estimada para calcular a nota esperada no exame de um aluno, com base no número de horas de estudo. Por exemplo, um aluno que estuda três horas deverá obter nota 82,91 no exame:

Nota do exame = 67,16 + 5,2503*(3) = 82,91

Regressão Linear Múltipla no Planilhas Google

Suponha que queiramos saber se o número de horas de estudo e o número de exames preparatórios realizados afetam a nota que um aluno obtém em determinado vestibular.

Para explorar essa relação, podemos realizar uma regressão linear múltipla utilizando horas estudadas e exames preparatórios tomados como variáveis explicativas e resultados de exames como variável resposta.

A captura de tela a seguir mostra como realizar a regressão linear múltipla usando um conjunto de dados de 20 alunos com a seguinte fórmula usada na célula E2:

= DIREITO ( C2:C21 , A2:B21 , VERDADEIRO , VERDADEIRO )

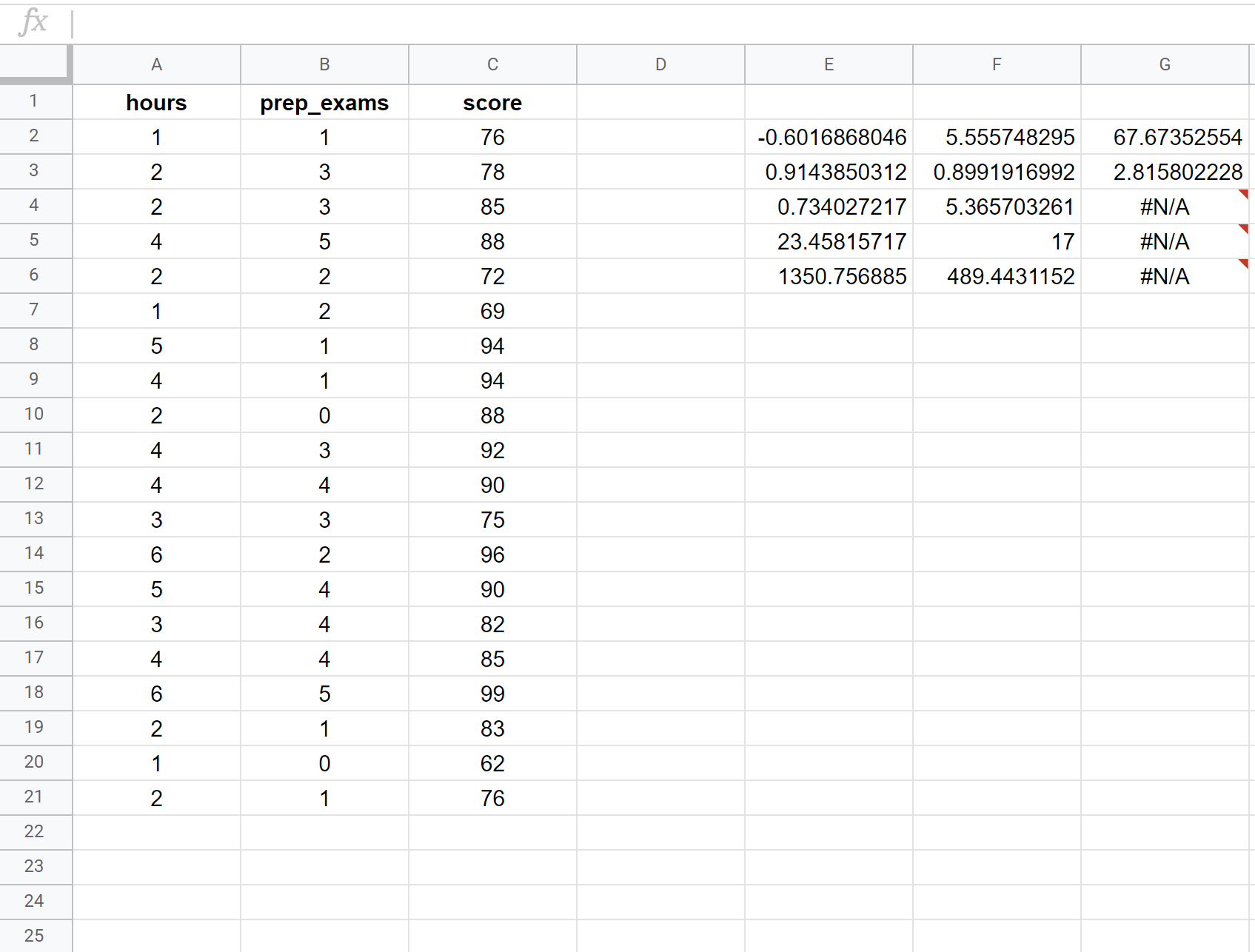
Veja como interpretar os números mais relevantes no resultado:

R Quadrado: 0,734 . Isso é chamado de coeficiente de determinação. É a proporção da variância da variável resposta que pode ser explicada pelas variáveis explicativas. Neste exemplo, 73,4% da variação nas notas dos exames é explicada pela quantidade de horas estudadas e pela quantidade de exames preparatórios realizados.

Erro padrão: 5,3657 . Esta é a distância média entre os valores observados e a linha de regressão. Neste exemplo, os valores observados desviam-se em média 5,3657 unidades da linha de regressão.

Equação de regressão estimada: podemos usar os coeficientes do resultado do modelo para criar a seguinte equação de regressão estimada:

Nota do exame = 67,67 + 5,56*(horas) – 0,60*(exames preparatórios)

Podemos usar esta equação de regressão estimada para calcular a pontuação esperada no exame de um aluno, com base no número de horas de estudo e no número de exames práticos que ele faz. Por exemplo, um aluno que estuda três horas e faz um exame preparatório deverá obter nota 83,75 :

Nota do exame = 67,67 + 5,56*(3) – 0,60*(1) = 83,75

Recursos adicionais

Os tutoriais a seguir explicam como realizar outras tarefas comuns no Planilhas Google:

Como realizar regressão polinomial no Planilhas Google
Como criar um gráfico residual no Planilhas Google