O que é uma pontuação z modificada? (definição e #038; exemplo)

Nas estatísticas, uma pontuação z nos diz quantos desvios padrão um valor está da média . Usamos a seguinte fórmula para calcular uma pontuação z:

Pontuação Z = (x _i – μ) / σ

Ouro:

• x _i : um único valor de dados
• μ: a média do conjunto de dados
• σ: o desvio padrão do conjunto de dados

As pontuações Z são frequentemente usadas para detectar valores discrepantes em um conjunto de dados. Por exemplo, observações com pontuação z menor que -3 ou maior que 3 são frequentemente consideradas discrepantes.

No entanto, as pontuações z podem ser afetadas por valores de dados excepcionalmente grandes ou pequenos. É por isso que uma maneira mais robusta de detectar valores discrepantes é usar um z-score modificado , calculado da seguinte forma:

Escore z modificado = 0,6745 (x _i – x̃) / MAD

Ouro:

• x _i : um único valor de dados
• x̃: A mediana do conjunto de dados
• MAD: o desvio absoluto mediano do conjunto de dados

Um escore z modificado é mais robusto porque usa a mediana para calcular os escores z, em oposição à média,que é conhecida por ser influenciada por valores discrepantes .

Iglewicz e Hoaglin recomendam que valores com escores z modificados menores que -3,5 ou maiores que 3,5 sejam rotulados como possíveis valores discrepantes.

O exemplo passo a passo a seguir mostra como calcular pontuações z modificadas para um determinado conjunto de dados.

Etapa 1: crie os dados

Suponha que temos o seguinte conjunto de dados com 16 valores:

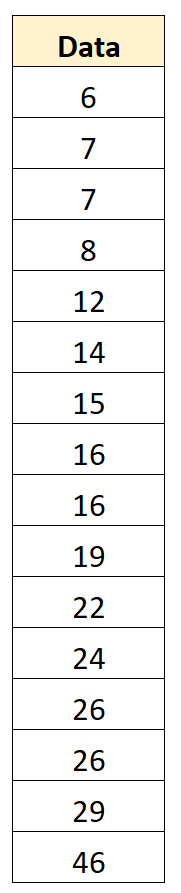
Etapa 2: Encontre a mediana

A seguir, encontraremos a mediana. Isso representa o ponto médio do conjunto de dados, que é 16 .

Etapa 3: Encontre a diferença absoluta entre cada valor e a mediana

A seguir, encontraremos a diferença absoluta entre cada valor de dados individual e a mediana. Por exemplo, a diferença absoluta entre o primeiro valor dos dados e a mediana é calculada da seguinte forma:

Diferença absoluta = |6 – 16| = 10

Podemos usar a mesma fórmula para calcular a diferença absoluta entre cada valor de dados individual e a mediana:

Etapa 4: Encontre o desvio mediano absoluto

A seguir, encontraremos o desvio mediano absoluto. Esta é a mediana da segunda coluna, que é 8 .

Etapa 5: Encontre a pontuação Z modificada para cada valor de dados

Finalmente, podemos calcular o escore z modificado para cada valor de dados usando a seguinte fórmula:

Escore z modificado = 0,6745 (x _i – x̃) / MAD

Por exemplo, a pontuação z modificada para o primeiro valor de dados é calculada da seguinte forma:

Escore z modificado = 0,6745*(6-16) / 8 = -0,843

Podemos repetir esta fórmula para cada valor no conjunto de dados:

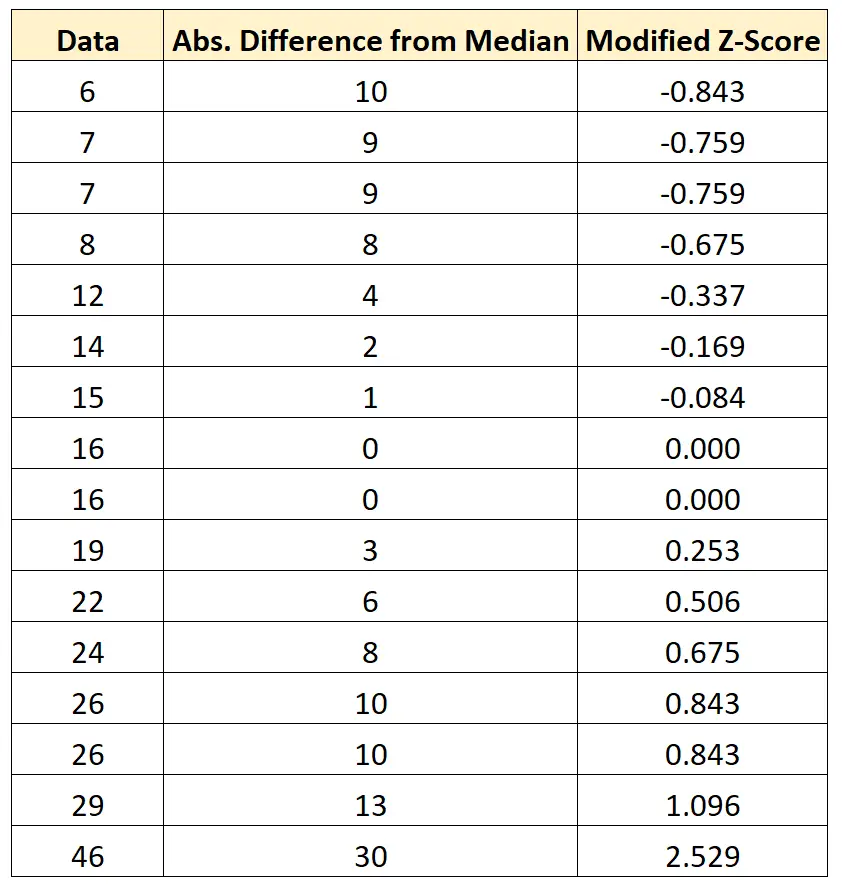
Podemos ver que nenhum valor no conjunto de dados tem uma pontuação z modificada menor que -3,5 ou maior que 3,5, portanto, não estamos rotulando nenhum valor neste conjunto de dados como um valor atípico em potencial.

Como lidar com outliers

Se um valor discrepante estiver presente em seu conjunto de dados, você terá várias opções:

• Certifique-se de que o valor discrepante não seja resultado de um erro de entrada de dados. Às vezes, um indivíduo simplesmente insere o valor errado dos dados ao salvar os dados. Se houver um valor discrepante, primeiro verifique se o valor foi inserido corretamente e se não houve um erro.
• Atribua um novo valor ao outlier . Se o valor discrepante for o resultado de um erro de entrada de dados, você pode decidir atribuir a ele um novo valor, como a média ou mediana do conjunto de dados.
• Remova o valor discrepante. Se o valor for realmente atípico, você poderá optar por removê-lo se ele tiver um impacto significativo em sua análise geral. Apenas certifique-se de mencionar em seu relatório ou análise final que você removeu um valor discrepante.