Por que as estatísticas são importantes? (10 razões pelas quais as estatísticas são importantes!)

O campo da estatística preocupa-se com a coleta, análise, interpretação e apresentação de dados.

À medida que a tecnologia se torna cada vez mais presente nas nossas vidas quotidianas, são gerados e recolhidos mais dados do que nunca na história da humanidade.

A estatística é a área que pode nos ajudar a entender como utilizar esses dados para realizar as seguintes tarefas:

• Compreender melhor o mundo que nos rodeia.
• Tome decisões usando dados.
• Faça previsões sobre o futuro usando dados.

Neste artigo, compartilhamos 10 razões pelas quais o campo da estatística é tão importante na vida moderna.

Razão 1: Use estatísticas descritivas para compreender o mundo

Estatísticas descritivas são usadas para descrever um dado bruto. Existem três tipos principais de estatísticas descritivas:

• Estatísticas resumidas
• Gráficos
• as mesas

Cada um desses elementos pode nos ajudar a compreender melhor os dados existentes.

Por exemplo, digamos que temos um conjunto de dados brutos mostrando as notas dos testes de 10.000 alunos em uma determinada cidade. Podemos usar estatísticas descritivas para:

• Calcule a pontuação média do teste e o desvio padrão dos resultados do teste.
• Gere um histograma ou boxplot para visualizar a distribuição dos resultados do teste.
• Crie uma tabela de frequência para entender a distribuição dos resultados dos testes.

Ao usar estatísticas descritivas, podemos entender as pontuações dos testes dos alunos com muito mais facilidade do que apenas observar os dados brutos.

Razão 2: Cuidado com gráficos enganosos

Cada vez mais gráficos estão sendo gerados em jornais, mídia, artigos online e revistas. Infelizmente, os gráficos muitas vezes podem ser enganosos se você não compreender os dados subjacentes.

Por exemplo, suponha que um periódico publique um estudo que encontra uma correlação negativa entre as pontuações GPA e ACT dos alunos de uma determinada universidade.

No entanto, esta correlação negativa só ocorre porque os estudantes que têm uma pontuação elevada no GPA e no ACT são capazes de frequentar uma universidade de elite, enquanto os estudantes que têm uma pontuação baixa no GPA e no ACT não são admitidos de todo.

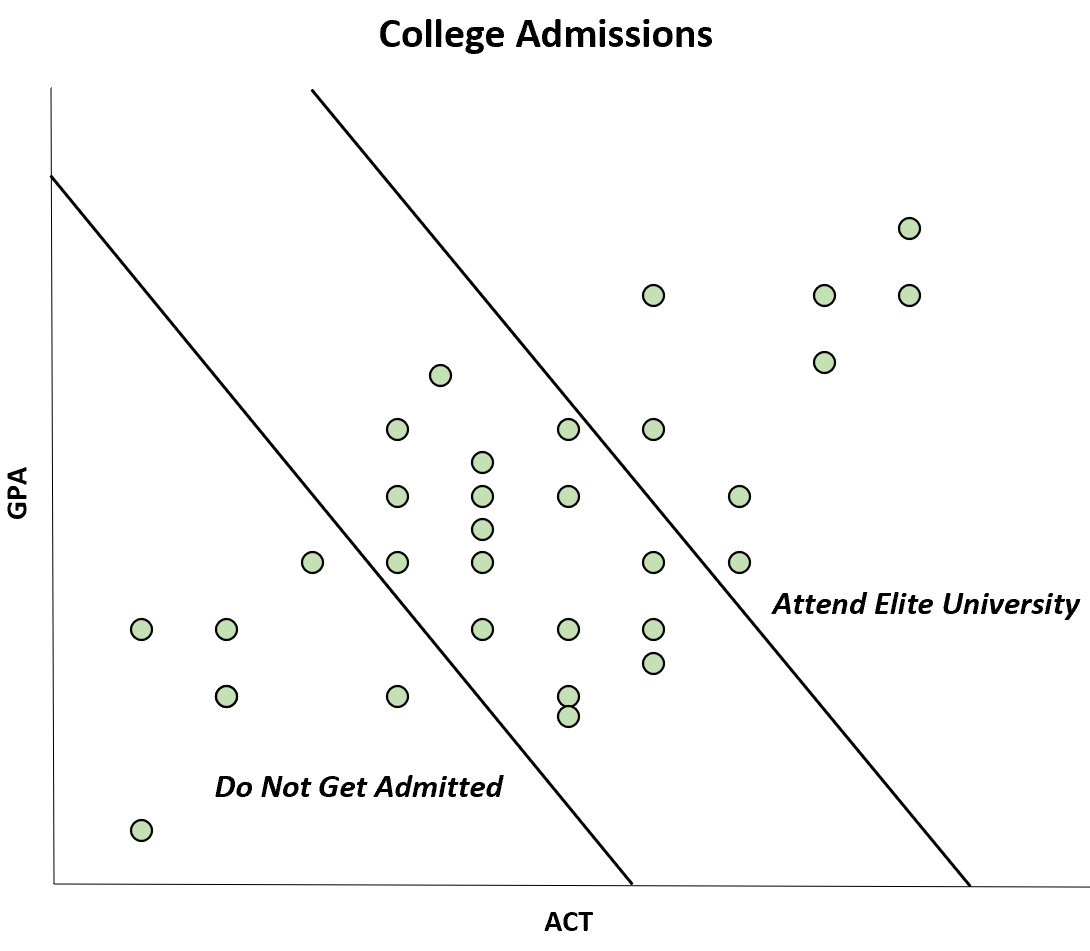
Embora a correlação entre ACT e GPA seja positiva na população, a correlação parece negativa na amostra.

Este viés específico é conhecido como viés de Berkson . Ao estar ciente desse viés, você pode evitar ser enganado por determinados gráficos.

Razão 3: tenha cuidado com variáveis confusas

Um conceito importante que você aprenderá em estatística é o conceito de variáveis confusas .

São variáveis que não são levadas em consideração e podem confundir os resultados de um experimento e levar a conclusões não confiáveis.

Por exemplo, suponha que um pesquisador colete dados sobre vendas de sorvetes e ataques de tubarões e descubra que as duas variáveis estão altamente correlacionadas. Isso significa que o aumento das vendas de sorvetes está causando mais ataques de tubarões?

É improvável. A causa mais provável é a confusa temperatura variável. Quando está mais quente lá fora, mais pessoas compram sorvete e mais pessoas vão para o mar.

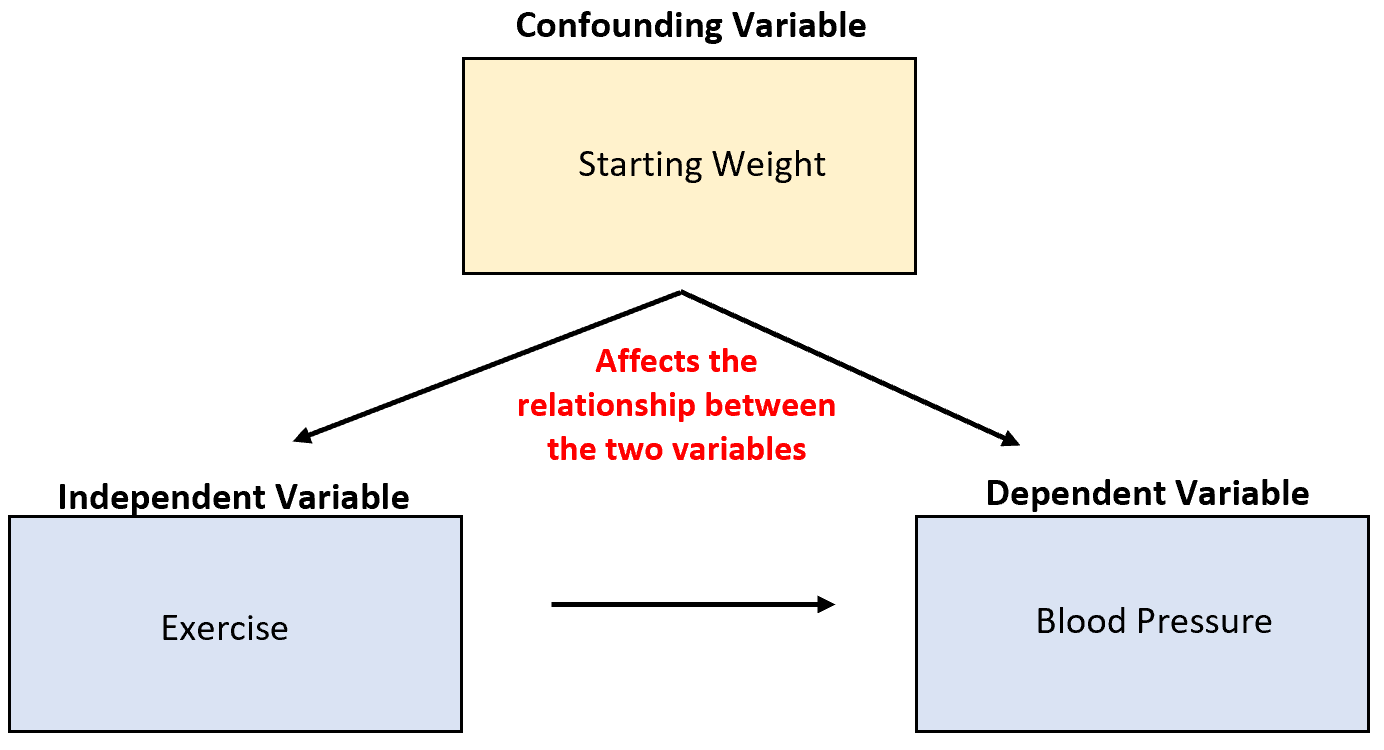
Razão 4: tomar melhores decisões usando probabilidades

Um dos subcampos mais importantes da estatística é a probabilidade . É o campo que estuda a probabilidade de ocorrência de eventos.

Ao ter uma compreensão básica de probabilidade, você pode tomar decisões mais informadas no mundo real.

Por exemplo, suponha que um estudante do ensino médio saiba que tem 10% de chance de ser aceito em uma determinada universidade. Usando a fórmula da probabilidade de aprovação em “pelo menos uma” , esse aluno pode encontrar a probabilidade de ser aceito em pelo menos uma universidade para a qual se inscreve e pode ajustar o número de universidades para as quais se inscreve por resultado.

Razão 5: Compreendendo os valores P na pesquisa

Outro conceito importante que você aprenderá em estatística são os valores-p .

A definição clássica de um valor p é:

Um valor p é a probabilidade de observar uma estatística de amostra que seja pelo menos tão extrema quanto sua estatística de amostra, dado que a hipótese nula é verdadeira.

Por exemplo, suponha que uma fábrica afirme produzir pneus com peso médio de 200 libras. Um auditor levanta a hipótese de que o peso médio real dos pneus produzidos nesta fábrica é diferente em 200 libras. Então ele realiza um teste de hipótese e descobre que o valor p do teste é 0,04.

Veja como interpretar esse valor p:

Se a fábrica realmente produz pneus com peso médio de 200 libras, então 4% de todas as auditorias atingirão o efeito observado na amostra, ou mais, devido a erro de amostragem aleatória. Isso nos diz que a obtenção dos dados amostrais obtidos pelo auditor seria bastante rara se a fábrica realmente produzisse pneus com peso médio de 200 libras.

Assim, o auditor provavelmente rejeitaria a hipótese nula de que o peso médio real dos pneus produzidos nesta fábrica é de facto de 200 libras.

Razão 6: Entenda a correlação

Outro conceito importante que você aprenderá em estatística é a correlação , que nos indica a associação linear entre duas variáveis.

O valor de um coeficiente de correlação está sempre entre -1 e 1 onde:

• -1 indica uma correlação linear perfeitamente negativa entre duas variáveis
• 0 indica nenhuma correlação linear entre duas variáveis
• 1 indica uma correlação linear perfeitamente positiva entre duas variáveis

Ao compreender esses valores, você pode compreender a relação entre as variáveis no mundo real.

Por exemplo, se a correlação entre gastos com publicidade e receitas for 0,87, então você poderá entender que existe uma forte relação positiva entre as duas variáveis. À medida que você gasta mais dinheiro em publicidade, pode esperar um aumento previsível na receita.

Razão 7: Faça previsões sobre o futuro

Outra razão importante para aprender estatística é compreender modelos básicos de regressão, como:

• Regressão linear simples
• Regressão linear múltipla
• Regressão logística

Cada um desses modelos permite fazer previsões sobre o valor futuro de uma variável de resposta com base no valor de determinadas variáveis preditoras no modelo.

Por exemplo, as empresas usam modelos de regressão linear múltipla no mundo real o tempo todo ao usar variáveis preditoras como idade, renda, etnia, etc. para prever quantos clientes gastarão em suas lojas.

Da mesma forma, as empresas de logística utilizam variáveis preditivas como demanda total, tamanho da população, etc. para prever vendas futuras.

Não importa em que área você atue, há uma boa chance de que modelos de regressão sejam usados para prever um fenômeno futuro.

Razão 8: Compreenda o potencial viés nos estudos

Outra razão para estudar estatísticas é estar ciente de todos os diferentes tipos de preconceitos que podem surgir em estudos do mundo real.

aqui estão alguns exemplos:

• Observe o preconceito
• Viés de autosseleção
• Viés de referência
• Viés de variável omitida
• Viés de subcontagem
• Viés de não resposta

Ao ter uma compreensão básica desses tipos de preconceitos, você pode evitar cometê-los ao conduzir pesquisas ou estar ciente deles ao ler outros artigos ou estudos de pesquisa.

Razão 9: Compreenda as suposições feitas pelos testes estatísticos

Muitos testes estatísticos fazem suposições sobre os dados subjacentes que estão sendo estudados.

Ao ler os resultados de um estudo ou mesmo ao conduzir o seu próprio estudo, é importante compreender quais suposições precisam ser feitas para que os resultados sejam confiáveis.

Os artigos a seguir compartilham as suposições feitas em muitos testes e procedimentos estatísticos comumente usados:

• Qual é a suposição de variância igual nas estatísticas?
• Qual é a suposição de normalidade nas estatísticas?
• Qual é a suposição de independência nas estatísticas?

Razão 10: Para evitar generalização excessiva

Outra razão para estudar estatística é compreender o conceito de generalização excessiva .

Isto ocorre quando os indivíduos que participam num estudo não são representativos dos indivíduos da população em geral e, portanto, é inadequado generalizar os resultados de um estudo para toda a população.

Por exemplo, digamos que queremos saber que porcentagem de alunos de uma determinada escola prefere “drama” como gênero de filme favorito. Se a população estudantil total for uma mistura de 50% de rapazes e 50% de raparigas, então uma amostra composta por 90% de rapazes e 10% de raparigas poderia levar a resultados tendenciosos se um número significativamente menor de rapazes preferir o teatro como género favorito.

Idealmente, queremos que a nossa amostra se assemelhe a uma “miniversão” da nossa população. Assim, se a população estudantil global for composta por 50% de raparigas e 50% de rapazes, a nossa amostra não seria representativa se incluísse 90% de rapazes e apenas 10% de raparigas.

Assim, quer esteja a realizar o seu próprio inquérito ou a ler os resultados de um inquérito, é importante compreender se os dados da amostra são representativos da população total e se os resultados do inquérito podem ser generalizados para a população com confiança.

Recursos adicionais

Confira os seguintes artigos para obter uma compreensão básica dos conceitos mais importantes em estatística introdutória:

Estatísticas descritivas ou inferenciais
População vs. amostra
Estatísticas versus parâmetros
Variáveis qualitativas e quantitativas
Níveis de medição: nominal, ordinal, intervalo e razão