Por que o desvio padrão é importante? (explicação + exemplos)

O desvio padrão é usado para medir a distribuição dos valores em uma amostra.

Podemos usar a seguinte fórmula para calcular o desvio padrão de uma determinada amostra:

√ Σ( _xi – x _barra ) ² / (n-1)

Ouro:

• Σ: Um símbolo que significa “soma”
• x _i : o i- ^ésimo valor da amostra
• x _bar : A amostra significa
• n: O tamanho da amostra

Quanto maior o valor do desvio padrão, mais dispersos são os valores em uma amostra. Por outro lado, quanto menor o valor do desvio padrão, mais próximos os valores estão agrupados.

Uma pergunta que os alunos costumam fazer é: Por que o desvio padrão é importante?

A resposta: O desvio padrão é importante porque nos informa a distribuição dos valores em um determinado conjunto de dados.

analisamos um conjunto de dados sempre que queremos encontrar as seguintes métricas:

• O centro do conjunto de dados . A maneira mais comum de medir o “centro” é usando a média e a mediana.
• A distribuição de valores no conjunto de dados . A forma mais comum de medir o spread é usar o desvio padrão.

Sabendo onde está o centro e qual é a distribuição dos valores, podemos entender bem a distribuição dos valores em qualquer conjunto de dados.

Os exemplos a seguir ilustram a importância do desvio padrão na prática.

Exemplo 1: Distribuição salarial

Suponha que o salário médio na empresa A seja de US$ 80.000 e o desvio padrão seja de US$ 20.000. Como o desvio padrão é tão grande, não há garantia de que você receberá perto de US$ 80.000 por ano se trabalhar nesta empresa, porque existe essa variação nos salários.

Por outro lado, suponha que o salário médio na Empresa B também seja de US$ 80.000, mas o desvio padrão seja de apenas US$ 4.000. Como esse desvio padrão é tão pequeno, você pode ter certeza de que receberá perto de US$ 80.000, pois há muito pouca variação nos salários.

Se criássemos um boxplot para visualizar a distribuição salarial nessas duas empresas, ficaria assim:

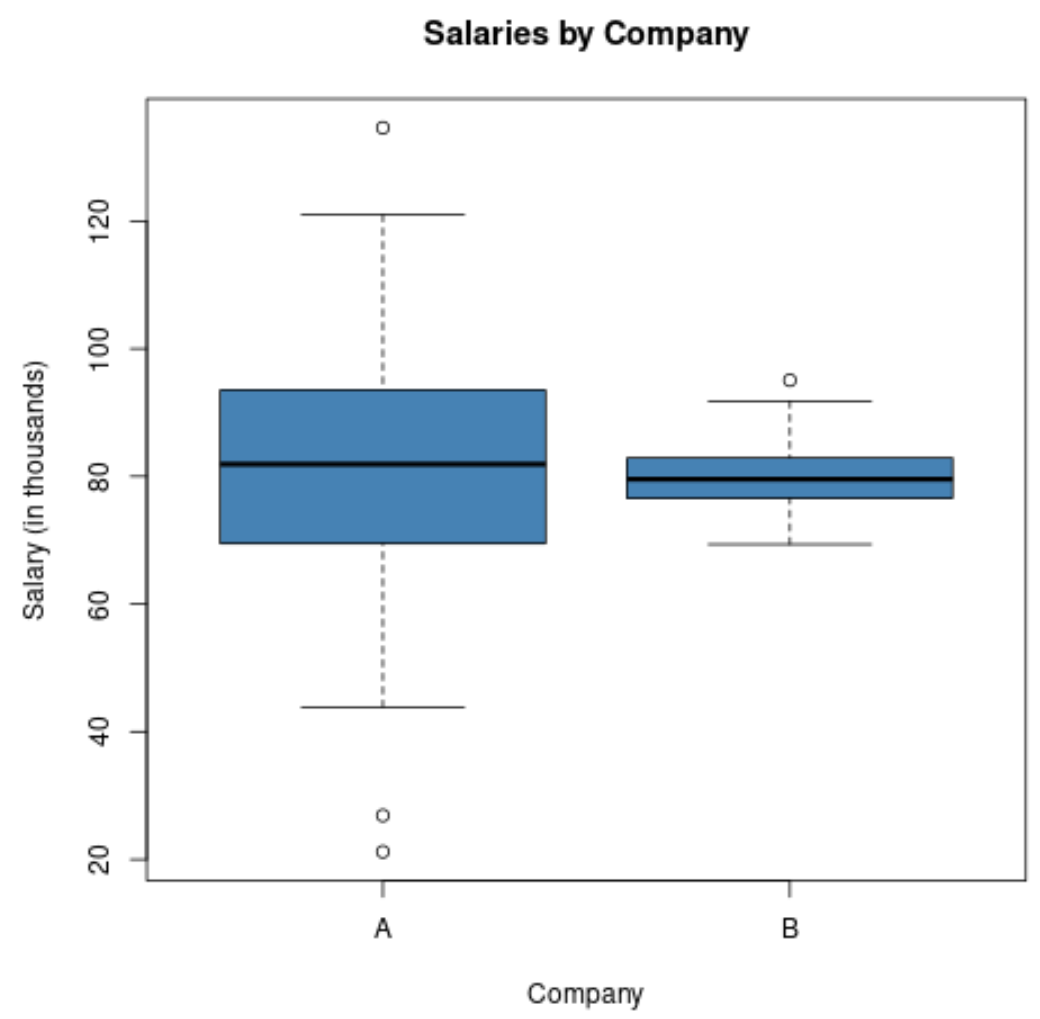
Observe que o comprimento do boxplot para a empresa A é maior, pois o desvio padrão dos salários é muito maior.

Ambas as empresas têm o mesmo salário médio, mas a diferença salarial é muito maior na empresa A.

Exemplo 2: Distribuição dos preços da habitação

Suponha que o preço médio da habitação no bairro A seja de US$ 250.000 e o desvio padrão seja de US$ 50.000. Como o desvio padrão é bastante grande, isso significa que alguns preços de casas serão muito superiores a US$ 250.000 e outros serão muito mais baixos. Se você olhar para qualquer casa neste bairro, não há garantia de que o preço estará próximo da média.

Por outro lado, suponha que o preço médio da casa no bairro B também seja de US$ 250.000, mas o desvio padrão seja de apenas US$ 10.000. Como esse desvio padrão é bem pequeno, você pode ter certeza de que qualquer casa que você olhar na vizinhança provavelmente estará fechada por esse preço.

Se criássemos um boxplot para visualizar a distribuição dos preços das casas nesses dois bairros, ele ficaria assim:

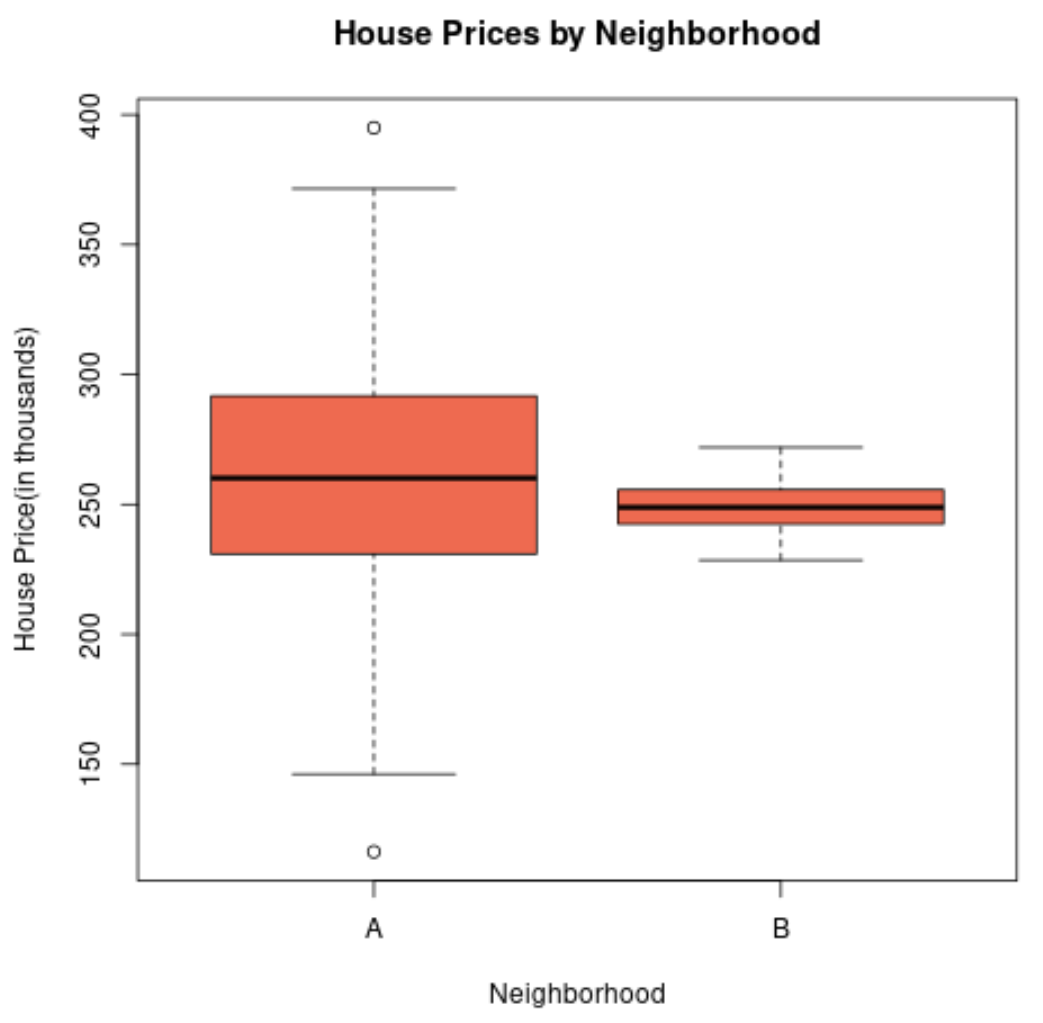
O comprimento do boxplot do bairro A é maior porque o desvio padrão dos preços dos imóveis é muito maior.

Na verdade, os preços das moradias variam de menos de US$ 150.000 a mais de US$ 400.000 para o bairro A, enquanto os preços variam apenas de cerca de US$ 230.000 a US$ 270.000 para o bairro B.

Simplesmente conhecendo o desvio padrão dos preços das casas em cada bairro, podemos saber quanta variação esperar nos preços em cada bairro.

Recursos adicionais

O que é considerado um bom desvio padrão?
Alcance vs. Desvio padrão: quando usar cada um
Coeficiente de variação versus desvio padrão: a diferença