O que é precisão equilibrada? (definição e #038; exemplo)

A precisão equilibrada é uma métrica que podemos usar para avaliar o desempenho de um modelo de classificação .

É calculado da seguinte forma:

Precisão Balanceada = (Sensibilidade + Especificidade) / 2

Ouro:

• Sensibilidade : A “taxa de verdadeiros positivos” – a porcentagem de casos positivos que o modelo é capaz de detectar.
• Especificidade : A “taxa de verdadeiros negativos” – a porcentagem de casos negativos que o modelo é capaz de detectar.

Esta métrica é particularmente útil quando as duas classes estão desequilibradas, ou seja, uma classe aparece muito mais que a outra.

O exemplo a seguir mostra como calcular a precisão balanceada na prática e demonstra por que ela é uma métrica tão útil.

Exemplo: Calculando a precisão balanceada

Suponha que um analista esportivo use um modelo de regressão logística para prever se 400 jogadores diferentes de basquete universitário serão ou não convocados para a NBA.

A seguinte matriz de confusão resume as previsões feitas pelo modelo:

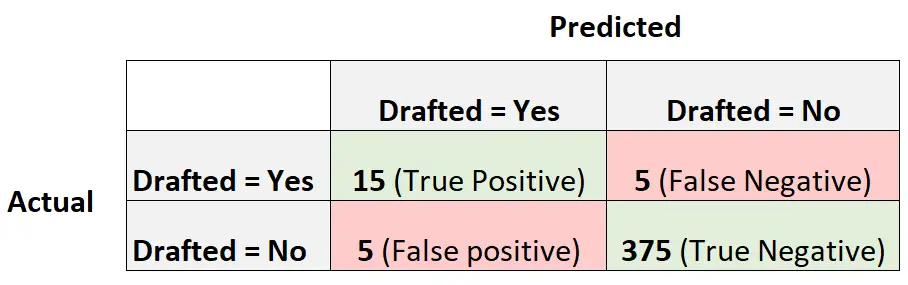
Para calcular a precisão balanceada do modelo, primeiro calcularemos a sensibilidade e a especificidade:

• Sensibilidade : A “taxa de verdadeiro positivo” = 15 / (15 + 5) = 0,75
• Especificidade : A “taxa verdadeiramente negativa” = 375 / (375 + 5) = 0,9868

Podemos então calcular a precisão balanceada da seguinte forma:

• Precisão Balanceada = (Sensibilidade + Especificidade) / 2
• Precisão balanceada = (0,75 + 9868) / 2
• Precisão balanceada = 0,8684

A precisão balanceada do modelo é 0,8684 .

Observe que quanto mais próxima a precisão balanceada estiver de 1, mais o modelo será capaz de classificar corretamente as observações.

Neste exemplo, a precisão equilibrada é bastante alta, o que nos diz que o modelo de regressão logística está fazendo um trabalho muito bom ao prever se os jogadores universitários serão ou não convocados para a NBA.

Neste cenário, como as classes são muito desequilibradas (20 jogadores foram convocados e 380 jogadores não), a precisão equilibrada nos dá uma imagem mais realista do desempenho do modelo em comparação com uma medida de precisão geral.

Por exemplo, calcularíamos a precisão do modelo da seguinte forma:

• Precisão = (TP + TN) / (TP + TN + FP + FN)
• Precisão = (15 + 375) / (15 + 375 + 5 + 5)
• Precisão = 0,975

A precisão do modelo é de 0,975 , o que parece extremamente alto.

No entanto, considere um modelo que simplesmente prevê que todos os jogadores não serão draftados. Teria uma precisão de 380/400 = 0,95 . Isso é apenas um pouco menor que a precisão do nosso modelo.

A pontuação de precisão balanceada de 0,8684 nos dá uma ideia melhor da capacidade do modelo de prever ambas as classes.

Em outras palavras, nos dá uma ideia melhor da capacidade do modelo de prever quais jogadores não serão draftados e quais irão.

Recursos adicionais

Os tutoriais a seguir explicam como criar uma matriz de confusão em diferentes softwares estatísticos:

Como criar uma matriz de confusão no Excel
Como criar uma matriz de confusão em R
Como criar uma matriz de confusão em Python