Probabilidade condicional (ou probabilidade condicional)

By Agosto 6, 2023 Probabilidade 0 Comments

Aqui você descobrirá o que é probabilidade condicional (ou probabilidade condicional). Explicamos como a probabilidade condicional é calculada com um exemplo e as propriedades deste tipo de probabilidade. Além disso, você poderá praticar exercícios de probabilidade condicional resolvidos passo a passo.

O que é probabilidade condicional?

Probabilidade condicional , também chamada de probabilidade condicional , é uma medida estatística que indica a probabilidade de que o evento A ocorra se outro evento B ocorrer. Ou seja, a probabilidade condicional P(A|B) refere-se à probabilidade do evento A ocorrer após o evento B já ter ocorrido.

A probabilidade condicional é escrita com uma barra vertical entre os dois eventos: P(A|B), e diz: “a probabilidade condicional do evento A dado o evento B”.

Observe que o valor da probabilidade condicional é um número entre 0 e 1. Quanto maior a probabilidade condicional, maior a probabilidade de o evento A ocorrer quando o evento B ocorrer, mas quanto menor a probabilidade condicional, menor a probabilidade de o evento A ocorrer. ocorrerá quando o evento B ocorrer.

Fórmula de Probabilidade Condicional

A probabilidade condicional do evento A dado o evento B é igual à probabilidade da interseção entre o evento A e o evento B dividida pela probabilidade do evento B.

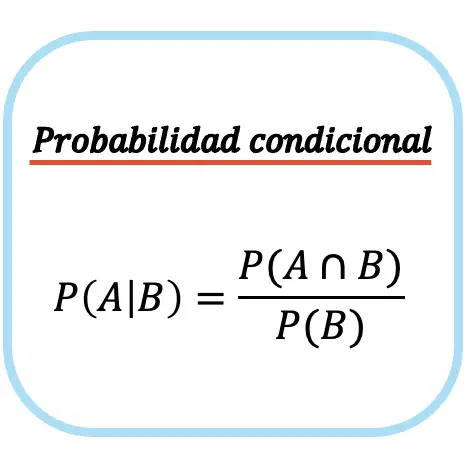
probabilidade condicional ou condicional

Observe que a fórmula de probabilidade condicional (ou probabilidade condicional) só pode ser usada se a probabilidade de ocorrência do evento incondicionado for diferente de zero, ou seja, P(B)≠0. Ou, em outras palavras, se é possível que o evento B ocorra.

A probabilidade condicional também pode ser calculada a partir do seu inverso, ou seja, se P(B|A) for conhecido, P(A|B) pode ser determinado. Mas para fazer isso você deve aplicar o teorema de Bayes, você pode ver em que consiste esse teorema aqui:

Exemplo de probabilidade condicional

Depois de vermos qual é a definição e fórmula da probabilidade condicional, resolveremos passo a passo um exemplo deste tipo de probabilidade para compreender completamente o seu significado.

  • Depois de fazer um exame em uma turma de 30 alunos, foram coletados dados para saber quantos alunos estudaram e quantos foram aprovados. Os resultados são apresentados na tabela de contingência a seguir. A partir dos dados coletados, calcule a probabilidade condicional de aprovação em um exame caso você já tenha estudado.
exercício de probabilidade condicional resolvido

Para obter a probabilidade condicional, devemos aplicar a fórmula que vimos anteriormente:

P(\text{aprobado}|\text{estudiado})=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}

Portanto, primeiro precisamos encontrar a probabilidade de um aluno ter estudado, estudado e aprovado. Para encontrar a probabilidade de um aluno ter estudado basta usar a regra de Laplace, ou seja, dividir o número de alunos que estudaram pelo número total de observações:

P(\text{estudiado})=\cfrac{23}{30}=0,77

E podemos descobrir a probabilidade de um aluno ter estudado e aprovado ao mesmo tempo na tabela de contingência dividindo o número de alunos que estudaram e aprovados pelo total:

P(\text{aprobado}\cap \text{estudiado})=\cfrac{19}{30}=0,63

Assim, a probabilidade de um aluno passar em um exame se tiver estudado é:

\begin{aligned}P(\text{aprobado}|\text{estudiado})&=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}\\ &=\cfrac{0,63}{0,77}\\[1.5ex] &=0,82\end{aligned}

Probabilidade condicional de eventos dependentes e independentes

Nesta seção veremos qual é a relação entre probabilidade condicional e eventos dependentes e independentes (ou eventos dependentes e independentes). Porque, embora sejam conceitos diferentes, estes dois tipos de eventos estão ligados a uma probabilidade condicional.

Dois eventos (ou ocorrências) são independentes quando a probabilidade de ocorrência não depende um do outro. Nesse caso, a intersecção entre os dois eventos é equivalente ao produto da probabilidade de cada evento separadamente. E, portanto, a fórmula da probabilidade condicional é simplificada:

P(A|B)=\cfrac{P(A\cap B)}{P(B)}=\cfrac{P(A)\cdot P(B)}{P(B)}=P(A)

Resumindo, se os eventos A e B são independentes, a probabilidade condicional do evento A dado o evento B é exatamente igual à probabilidade de ocorrência do evento A.

Por outro lado, quando dois eventos são dependentes, significa que a probabilidade de um evento depende da probabilidade do outro evento. Portanto, quando dois eventos A e B são dependentes, a probabilidade condicional do evento A dado o evento B é diferente da probabilidade de ocorrência do evento A.

P(A|B)\neq P(A)

Exercícios de probabilidade condicional resolvidos

Exercício 1

Sabemos que num saco cheio de bolas, metade é laranja e a outra metade é verde. Além disso, um terço de todas as bolas são laranja e ao mesmo tempo marcadas com um sinal. Qual é a probabilidade de que quando você tira uma bola laranja ela receba o sinal?

Para resolver o exercício, devemos aplicar a fórmula condicional de probabilidade, que é:

P(\text{se\~nal}|\text{naranja})=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}

A definição do problema nos diz que metade da sacola é composta de laranjas. Portanto, a probabilidade teórica de pegar uma bola laranja é de 50%.

P(\text{naranja})=\cfrac{1}{2}=0,5

Por outro lado, sabemos que um terço do total são bolas laranja e têm sinal, então a probabilidade de obter uma bola laranja com sinal é:

P(\text{se\~nal}\cap \text{naranja})=\cfrac{1}{3}=0,33

Finalmente, substituímos as probabilidades calculadas na fórmula de probabilidade condicional para encontrar seu valor:

\begin{aligned}P(\text{se\~nal}|\text{naranja})&=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}\\ &=\cfrac{0,33}{0,5}\\[1.5ex] &=0,66\end{aligned}

Em resumo, a probabilidade de tirar uma bola com o sinal laranja é de 66%.

Exercício 2

Se tivermos seis canetas azuis e três canetas pretas numa caixa, calcule a probabilidade de desenhar uma única caneta azul e a probabilidade de desenhar duas canetas azuis consecutivamente.

Para determinar a probabilidade de pegar uma caneta azul uma vez, basta usar a lei de Laplace:

P(\text{azul})=\cfrac{6}{6+3}=0,67

O problema também nos pede para saber a probabilidade de pegar duas canetas azuis consecutivamente, ou seja, a probabilidade condicional de pegar uma caneta azul se já tivermos pegado uma caneta azul antes.

Se desenharmos uma caneta azul, temos um caso menos favorável, mas também há uma caneta a menos no total. A probabilidade condicional é, portanto:

P(\text{azul}|\text{azul})=\cfrac{5}{8}=0,63

Exercício 3

Qual é a probabilidade condicional de lançar um dado até o número 4, dado que o lançamento de uma moeda resulta em cara?

Para resolver este exercício, deve-se levar em consideração a teoria da probabilidade condicional, pois os eventos “obter o número 4 jogando um dado” e “obter cara jogando uma moeda” são independentes. Portanto, não é necessário usar a fórmula de probabilidade condicional, mas a seguinte igualdade é satisfeita:

P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})

Então, para encontrar a probabilidade condicional, basta usar a regra de Laplace:

P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})=\cfrac{1}{6}=0,167

Exercício 4

Foi estudado o exercício financeiro de 25 empresas de um país e como os preços de suas ações mudam dependendo do resultado econômico do ano. Você pode ver os dados coletados na seguinte tabela de contingência:

exercício de probabilidade condicional resolvido

Qual a probabilidade de o preço das ações de uma empresa aumentar se ela obteve lucro no ano passado?

O exercício questiona-nos sobre a probabilidade condicional de as ações subirem, dado que a empresa obteve um resultado económico positivo. Então, para calcular essa probabilidade, devemos usar a fórmula de probabilidade condicional:

P(\text{precio sube}|\text{beneficio})=\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}

Portanto, calculamos primeiro a probabilidade de uma empresa obter lucro e, em segundo lugar, a probabilidade de uma empresa obter lucro económico enquanto aumenta o seu preço por ação:

P(\text{beneficio})=\cfrac{14}{25}=0,56

P(\text{precio sube}\cap\text{beneficio})=\cfrac{10}{25}=0,4

E então substituímos os valores encontrados na fórmula e calculamos a probabilidade condicional:

\begin{aligned}P(\text{precio sube}|\text{beneficio})& =\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}\\ &= \cfrac{0,4}{0,56}\\[1.5ex]& =0,71 \end{aligned}

Propriedades da probabilidade condicional

As propriedades da probabilidade condicional, ou probabilidade condicional, são as seguintes:

  • A soma da probabilidade condicional do evento A dado evento B mais a probabilidade condicional do evento complementar A dado evento B é igual a um.

P\bigl(A|B\bigr)+P\bigl(\overline{A}|B\bigr)=1

  • Se o evento A for um subconjunto do evento B, A sempre ocorrerá quando B for verdadeiro. Assim, a probabilidade condicional do evento A dado o evento B nesses casos é 1.

B\subseteq A \ \longrightarrow \ P(A|B)=1

  • Dados dois eventos diferentes, a seguinte igualdade em relação à probabilidade condicional sempre é válida:

P\bigl(A\bigr)=P\bigl(A|B\bigr)\cdot P\bigl(B\bigr)+P\bigl(A|\overline{B}\bigl)\cdot P\bigl(\overline{B}\bigr)

About Author

Dr. Benjamin Anderson
Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais

Add a Comment

O seu endereço de email não será publicado. Campos obrigatórios marcados com *