Probabilidade posterior: definição + exemplo

A probabilidade a posteriori é a probabilidade atualizada de que um evento ocorrerá após levar em conta novas informações.

Por exemplo, podemos estar interessados na probabilidade de um evento “A” ocorrer após contabilizar um evento “B” que acabou de ocorrer. Poderíamos calcular essa probabilidade posterior usando a seguinte fórmula:

P(A|B) = P(A) * P(B|A) / P(B)

Ouro:

P(A|B) = a probabilidade de ocorrência do evento A, dado que o evento B ocorreu. Observe que “| » significa “dado”.

P(A) = a probabilidade de que o evento A ocorra.

P(B) = a probabilidade de que o evento B ocorra.

P(B|A) = a probabilidade de ocorrência do evento B, dado que o evento A ocorreu.

Exemplo: Calculando a probabilidade posterior

Uma floresta é composta por 20% de carvalhos e 80% de bordos. Suponha que saibamos que 90% dos carvalhos são saudáveis, enquanto apenas 50% dos bordos são saudáveis. Suponha que, à distância, você possa dizer que uma determinada árvore está saudável. Qual é a probabilidade de a árvore ser um carvalho?

Lembre-se de que a probabilidade de o evento A ocorrer, dado que o evento B ocorreu, é:

P(A|B) = P(A) * P(B|A) / P(B)

Neste exemplo, a probabilidade de a árvore ser um carvalho, dado que a árvore é saudável, é:

P(Carvalho|Saudável) = P(Carvalho) * P(Saudável|Carvalho) / P(Saudável)

P(Carvalho) = A probabilidade de uma determinada árvore ser um carvalho é 0,2 porque 20% de todas as árvores da floresta são carvalhos.

P(Saudável) = A probabilidade de uma determinada árvore ser saudável pode ser calculada da seguinte forma: (0,20)*(0,9) + (0,8)*(0,5) = 0,58 .

P(Saudável|Carvalho) = A probabilidade de uma árvore ser saudável dado que é um carvalho é de 0,9 , uma vez que nos disseram que 90% dos carvalhos são saudáveis.

Usando esses três números, podemos encontrar a probabilidade de a árvore ser um carvalho, visto que é saudável:

P(Carvalho|Saudável) = P(Carvalho) * P(Saudável|Carvalho) / P(Saudável) = (0,2) * (0,9) / (0,58) = 0,3103 .

Para uma compreensão intuitiva desta probabilidade, vamos supor que a seguinte grelha representa esta floresta de 100 árvores. Exatamente 20 das árvores são carvalhos e 18 delas são saudáveis. As outras 80 árvores são bordos e 40 delas são saudáveis.

(O = Carvalho, M = Bordo, Verde = Saudável, Vermelho = Não saudável)

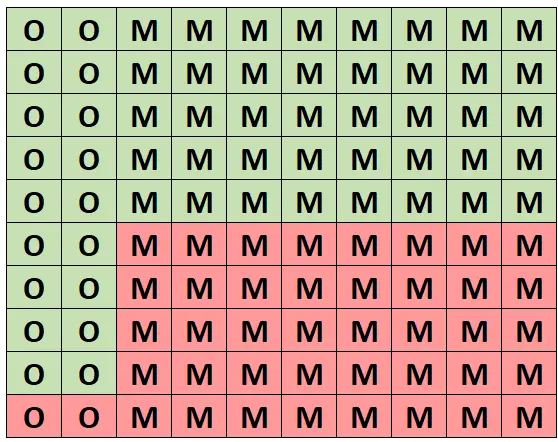
De todas as árvores, exatamente 58 delas são saudáveis e 18 dessas árvores saudáveis são carvalhos. Portanto, se soubermos que selecionamos uma árvore saudável, a probabilidade de ser um carvalho é 18/58 = 0,3103 .

Quando você deve usar a probabilidade posterior?

A probabilidade posterior é usada em uma ampla variedade de campos, incluindo finanças, medicina, economia e previsão do tempo.

O objetivo de usar probabilidades posteriores é atualizar uma crença anterior que tínhamos sobre algo, uma vez que obtivemos novas informações.

Lembre-se do exemplo anterior que sabíamos que a probabilidade de uma determinada árvore na floresta ser carvalho era de 20%. Isso é chamado de probabilidade anterior . Se simplesmente escolhêssemos uma árvore ao acaso, saberíamos que a probabilidade de ser um carvalho era de 0,20.

No entanto, assim que obtivemos a nova informação de que a árvore que selecionamos era saudável, pudemos utilizar esta nova informação para determinar que a probabilidade posterior desta árvore ser um carvalho era de 0,3103.

No mundo real, as pessoas estão constantemente descobrindo novas informações. Esta nova informação nos ajuda a atualizar nossas crenças anteriores. Em termos estatísticos, isto significa que somos capazes de gerar probabilidades posteriores de eventos que ocorrem, o que nos ajuda a obter uma compreensão mais precisa do mundo e permite-nos fazer previsões mais precisas sobre eventos futuros.