Um guia para o procedimento benjamini-hochberg

Sempre que você realiza um teste estatístico, é possível obter um valor p menor que 0,05 por puro acaso, mesmo que sua hipótese nula seja verdadeira.

Por exemplo, digamos que você queira saber se uma determinada planta tem uma altura média superior a 25 centímetros. Suas hipóteses nulas e alternativas para teste seriam:

H ₀ : μ = 10 polegadas

_HA : μ> 10 polegadas

Para testar essa hipótese, você pode coletar uma amostra aleatória de 20 plantas para medir. Embora a verdadeira altura média desta espécie de planta seja de 25 centímetros, é possível que você tenha selecionado uma amostra de 20 plantas excepcionalmente altas, o que o levou a rejeitar a hipótese nula.

Mesmo que a hipótese nula fosse verdadeira (a altura média desta planta era na verdade de 25 centímetros), você a rejeitou. Nas estatísticas, chamamos isso de “falsa descoberta”. Você afirma ter feito uma descoberta – um “resultado significativo” – mas isso é na verdade falso.

Agora imagine executar 100 testes estatísticos de uma só vez. Usando um nível alfa de 0,05, há apenas 5% de chance de fazer uma descoberta falsa com um teste individual, mas como você está fazendo um número tão grande de testes, seria de esperar que apenas cerca de 5 em 100 levassem a descobertas falsas.

No mundo moderno, as falsas descobertas podem ser um problema comum, uma vez que a tecnologia permitiu aos investigadores realizar centenas ou mesmo milhares de testes estatísticos de cada vez.

Por exemplo, os investigadores médicos podem realizar testes estatísticos em dezenas de milhares de genes de cada vez. Mesmo com uma taxa de descobertas falsas de apenas 5%, isso significa que centenas de testes podem resultar em descobertas falsas.

Uma maneira de controlar a taxa de falsas descobertas é usar o chamado procedimento de Benjamini-Hochberg.

O procedimento Benjamini-Hochberg

O procedimento Benjamini-Hochberg funciona da seguinte forma:

Passo 1: Execute todos os seus testes estatísticos e encontre o valor p para cada teste.

Passo 2: Classifique os valores-p em ordem decrescente, atribuindo uma classificação a cada um: o menor valor tem classificação 1, o próximo menor tem classificação 2, etc.

Etapa 3: Calcule o valor crítico de Benjamini-Hochberg para cada valor p, usando a fórmula (i/m)*Q

Ouro:

i = classificação do valor p

m = número total de testes

Q = taxa de descoberta falsa escolhida

Etapa 4: Encontre o maior valor p menor que o valor crítico. Designe cada valor p menor que esse valor p como significativo.

O exemplo a seguir ilustra como realizar este procedimento com valores concretos.

Exemplo

Digamos que os pesquisadores queiram determinar se 20 variáveis diferentes estão ou não relacionadas a doenças cardíacas. Eles realizam 20 testes estatísticos individuais por vez e recebem um valor p para cada teste. A tabela a seguir mostra os valores p de cada teste, listados em ordem decrescente.

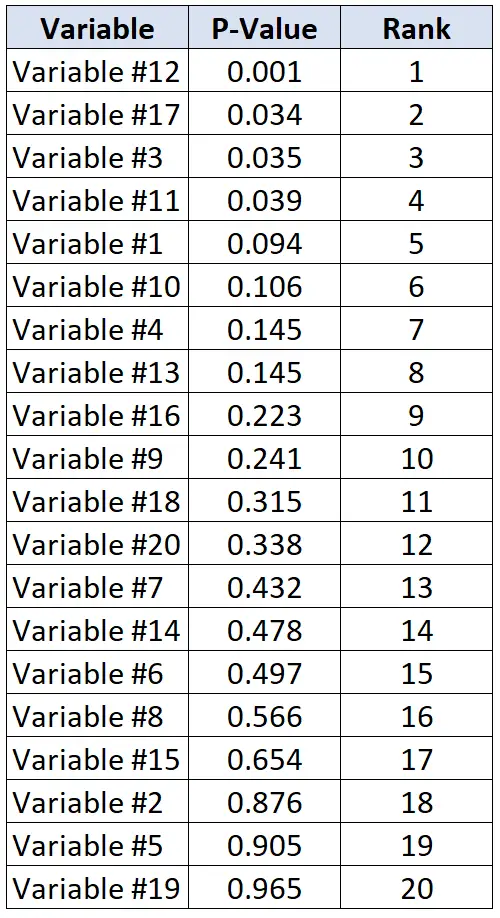
Suponha que os pesquisadores estejam dispostos a aceitar uma taxa de descoberta falsa de 20%. Assim, para calcular o valor crítico de Benjamini-Hochberg para cada valor p, podemos usar a seguinte fórmula: (i/20)*0,2 onde i = classificação do valor p.

A tabela a seguir mostra o valor crítico de Benjamini-Hochberg para cada valor p individual:

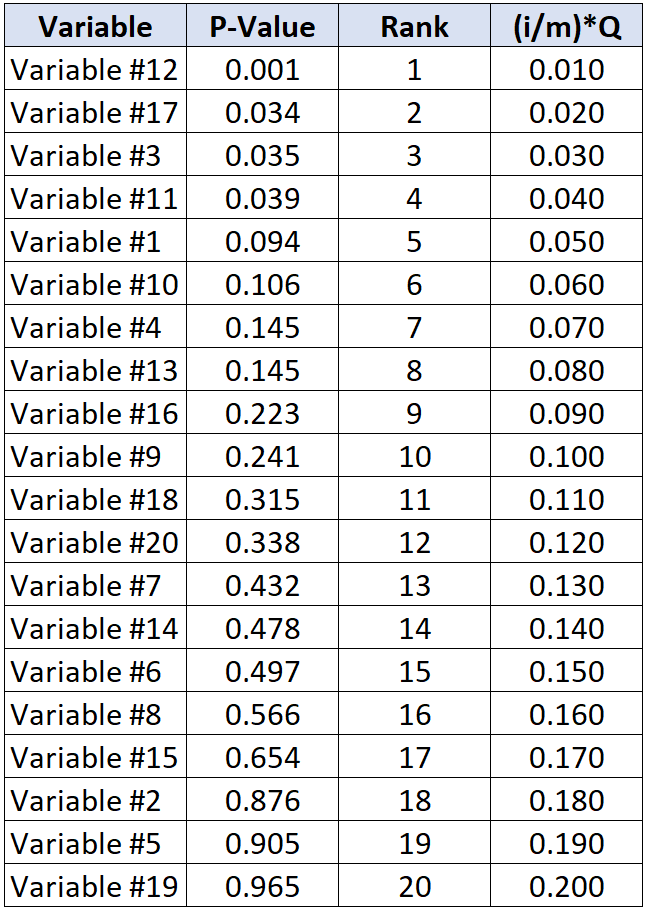
O teste com maior valor de p abaixo do valor crítico de Benjamini-Hochberg é a variável #11, que possui valor de p de 0,039 e valor crítico de BH de 0,040.

Assim, este teste e todos os testes com valor de p menor serão considerados significativos.

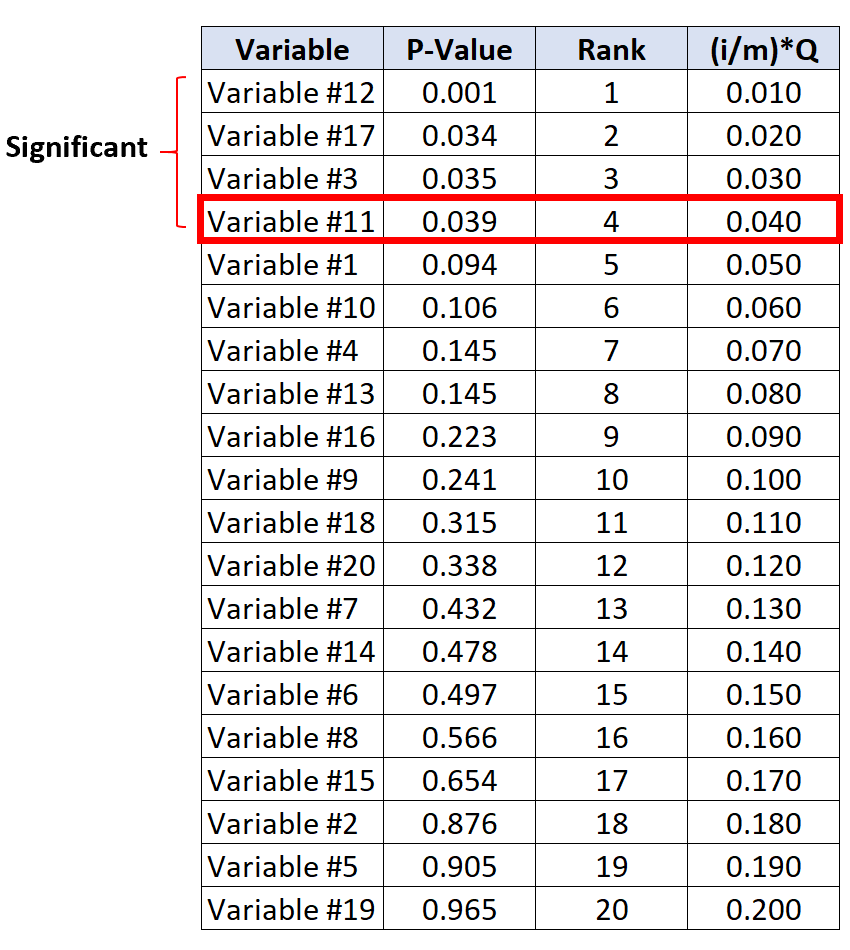
Observe que mesmo que as variáveis #17 e #3 não tenham valores de p menores que seus valores críticos de BH, elas ainda são consideradas significativas porque possuem valores de p menores que a variável #11.

Como escolher uma taxa de descoberta falsa

Um dos passos mais importantes no procedimento de Benjamini-Hochberg é escolher uma taxa de descoberta falsa. Você deve escolher sua taxa de descoberta falsa antes de coletar dados ou realizar testes estatísticos.

Normalmente, você realizará um grande número de testes estatísticos durante a fase exploratória de sua análise, que serão acompanhados por outros testes para explorar ainda mais seus resultados.

Se os testes de acompanhamento forem baratos, você poderá considerar definir uma taxa de descobertas falsas mais alta, porque mesmo que tenha algumas descobertas falsas, você provavelmente descobrirá essas descobertas falsas em testes subsequentes.

Além disso, se o custo de perder uma descoberta importante for alto, você pode querer aumentar sua taxa de falsas descobertas para não perder nada importante.

Dependendo dos custos da sua pesquisa e da importância de não perder nenhuma descoberta importante, a taxa de falsas descobertas variará de situação para situação.

Recursos adicionais

Uma explicação dos valores P e significância estatística
Qual é a taxa de erro por família?