Proporção da amostra

Este artigo explica o que é proporção de amostra em estatísticas. Assim, você descobrirá como calcular a proporção amostral, um exercício resolvido e, também, qual a diferença entre a proporção amostral e a proporção populacional.

Qual é a proporção da amostra?

A proporção da amostra é a proporção de casos de sucesso em uma amostra em relação ao tamanho da amostra. Portanto, para calcular a proporção da amostra, o número de sucessos na amostra deve ser dividido pelo número total de dados.

O símbolo para proporção da amostra é

.

Nas estatísticas, quando se realiza um inquérito, normalmente nem todos os dados populacionais são conhecidos, razão pela qual normalmente se realiza um estudo de uma amostra representativa e depois as conclusões tiradas são extrapoladas para toda a população. população. Assim, a proporção da amostra é usada para estimar a proporção de toda a população. Abaixo veremos como isso é feito.

Exemplo de fórmula de proporção

A proporção da amostra é igual ao número de casos de sucesso na amostra dividido pelo tamanho da amostra. Portanto, a fórmula para cálculo da proporção amostral é:

Ouro:

• 

  é a proporção da amostra.

• 

  é o número de casos de sucesso na amostra.

• 

  é o número total de itens de dados na amostra.

Exemplo de cálculo de proporção de amostra

Depois de ver a definição de proporção amostral e qual é sua fórmula, nesta seção resolveremos um exemplo simples para que você possa ver como a proporção amostral é calculada.

• Uma empresa fabrica um brinquedo e compra uma de suas peças de outra empresa externa. Porém, dentro dos lotes que compra aparecem peças defeituosas, por isso ele decide fazer um estudo estatístico para saber a proporção de peças em bom estado e a proporção de defeitos. Então, você pede uma amostra de 1.000 unidades e encontra 138 peças defeituosas. Qual é a proporção de peças em bom estado na amostra? E qual é a proporção de peças defeituosas na amostra?

O número de peças não danificadas na amostra é 1.000 menos o número de peças defeituosas:

Então, para encontrar a proporção amostral, aplicamos a fórmula que vimos acima:

A proporção da amostra de peças em bom estado é, portanto, de 86,2%.

Por outro lado, a proporção de peças defeituosas equivale a um menos a proporção de peças boas:

A proporção amostral de peças defeituosas é, portanto, de 13,8%.

Proporção da amostra e proporção da população

A proporção da população é a proporção da população estatística. Ou seja, a proporção populacional é a relação dos casos de sucesso de uma população estudada em relação a todos os elementos que fazem parte dessa população.

Portanto, a diferença entre a proporção nacional e a proporção populacional é que a proporção nacional é a proporção dos casos de maioria, em mudança, a proporção populacional refere-se à proporção de casos de eventos respeitando todos os elementos População.

Para diferenciar a proporção amostral da proporção populacional, elas são representadas por símbolos diferentes. O símbolo para proporção da amostra é

, enquanto o símbolo da proporção da população é

.

Em geral, a proporção populacional não pode ser determinada com precisão, porque nem todos os valores populacionais são normalmente conhecidos. Em vez disso, o valor da proporção da população é geralmente estimado utilizando um intervalo de confiança com a seguinte fórmula:

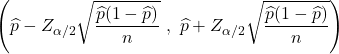
Para ver como a proporção da população é estimada, clique no seguinte link:

Distribuição amostral de proporções

Por fim, veremos em que consiste uma distribuição amostral de proporções, pois é um conceito estatístico relacionado à proporção amostral.

Primeiro, vamos começar definindo o que é uma distribuição amostral. Uma distribuição amostral é a distribuição que resulta da consideração de todas as amostras possíveis de uma população estatística.

Portanto, uma distribuição amostral de proporções é a distribuição que resulta do cálculo da proporção de cada amostra possível de uma população. Ou seja, se estudarmos todas as amostras possíveis de uma população e calcularmos a proporção de cada uma das amostras, o conjunto de valores calculado é uma distribuição amostral de proporções amostrais.