Raiz quadrada média

Aqui explicamos o que é a raiz quadrada média e como ela é calculada. Além disso, você aprenderá as vantagens e desvantagens de usar a média e um exercício resolvido passo a passo. Finalmente, você poderá calcular a raiz quadrada média de qualquer conjunto de dados com a calculadora no final do artigo.

Qual é o quadrado médio?

A raiz quadrada média é uma medida da centralidade da estatística descritiva. A raiz quadrada média é igual à raiz quadrada da média aritmética dos quadrados dos dados.

A raiz quadrada média também é chamada de raiz quadrada média ou RMS .

A fórmula para a média quadrática é, portanto, a seguinte:

A média quadrada é particularmente útil quando a variável estatística assume valores positivos e negativos, porque ao elevar ao quadrado cada dado, todos os valores se tornam positivos. Portanto, o quadrado médio é utilizado para analisar variáveis nas quais o sinal não é importante, mas sim o seu valor absoluto.

Por exemplo, o quadrado médio é usado para estudar erros de medição, porque nestes casos não estamos verificando se o erro é positivo ou negativo, mas sim analisando a magnitude do erro durante a medição.

Além disso, os quadrados dos números grandes têm valores muito mais elevados do que os quadrados dos números pequenos, portanto, no quadrado do meio, os números grandes são mais importantes do que os números pequenos.

A média quadrada é um tipo de média estatística junto com a média aritmética, a média ponderada, a média geométrica e a média harmônica.

Vantagens e desvantagens da raiz quadrada média

A média quadrática tem vantagens e desvantagens em comparação com outros tipos de médias.

A principal vantagem da média quadrática é que ela permite obter uma aproximação muito boa do valor médio de uma variável discreta. Por outro lado, a grande desvantagem da média quadrada é que o seu cálculo é bastante complicado, uma vez que devem ser realizadas diversas operações.

Em contraste, a raiz quadrada média é muito útil para analisar medições de erros. Também dá muito mais importância aos valores elevados, embora esta propriedade implique que uma medição errada alterará significativamente o resultado rms.

Como calcular a raiz quadrada média

Para calcular a raiz quadrada média, as seguintes etapas devem ser executadas:

1. Calcule o quadrado de cada dado estatístico.
2. Some todos os quadrados calculados na etapa anterior.
3. Divida o resultado pelo número de itens de dados na amostra.
4. Encontre a raiz quadrada do valor anterior.
5. O resultado obtido é a média quadrada da amostra estatística.

👉 Você pode usar a calculadora abaixo para calcular a raiz quadrada média de qualquer conjunto de dados.

Exemplo de quadrado médio

Depois de sabermos como obter a raiz quadrada média, determinaremos a raiz quadrada média de um conjunto de dados como exemplo.

• Numa aula de laboratório universitário, o professor pede aos seus alunos que façam uma experiência com produtos químicos. O objetivo do experimento químico é obter uma solução de 3 litros no total. Os grupos de alunos obtiveram os seguintes dados:

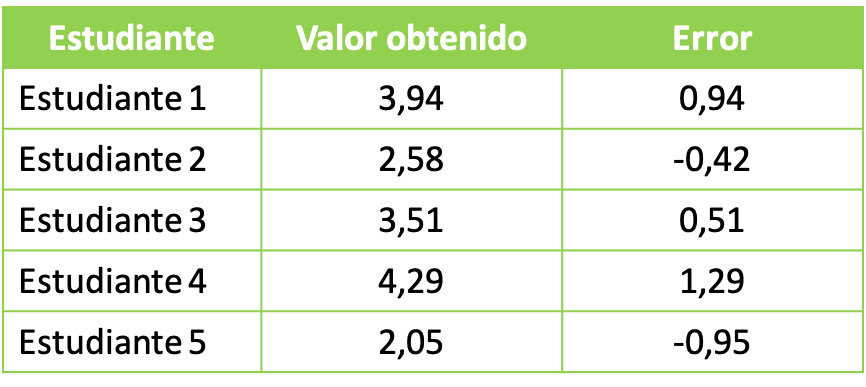
Para estudar os dados estatísticos obtidos, procede-se ao cálculo do valor da média quadrada com o erro obtido por cada grupo. Portanto, aplicamos a fórmula da média quadrática:

E substituímos os dados na fórmula e calculamos a raiz quadrada média:

Assim, o erro médio obtido no experimento, segundo a raiz quadrada média, é de 0,88 litros.

Calculadora Média Quadrada

Insira dados de qualquer amostra estatística na calculadora a seguir para calcular sua raiz quadrada média. Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.