Quando usar a correlação de classificação de spearman (2 cenários)

A forma mais comum de quantificar a associação linear entre duas variáveis é utilizar o coeficiente de correlação de Pearson , que assume sempre um valor entre -1 e 1 onde:

• -1 indica uma correlação linear perfeitamente negativa
• 0 indica nenhuma correlação linear
• 1 indica uma correlação linear perfeitamente positiva

No entanto, este tipo de coeficiente de correlação funciona melhor quando a verdadeira relação subjacente entre as duas variáveis é linear .

Existe outro tipo de coeficiente de correlação chamado correlação de classificação de Spearman que é melhor usado em dois cenários específicos:

Cenário 1 : Ao trabalhar com dados classificados.

• Um exemplo poderia ser um conjunto de dados contendo a classificação da nota do exame de matemática de um aluno, bem como a classificação da nota do exame de ciências em uma turma.

Cenário 2 : Quando um ou mais valores extremos estão presentes.

• Quando valores discrepantes extremos estão presentes em um conjunto de dados, o coeficiente de correlação de Pearson é bastante afetado.

Os exemplos a seguir mostram como calcular a correlação de classificação de Spearman em cada um desses cenários.

Cenário 1: Correlacionando a classificação de Spearman com dados classificados

Considere o seguinte conjunto de dados (e o gráfico de dispersão correspondente) que mostra a relação entre duas variáveis:

Usando software estatístico, podemos calcular os seguintes coeficientes de correlação para essas duas variáveis:

• Correlação de Pearson: 0,79
• Correlação de classificação de Spearman: 1

Nesse cenário, se nos importarmos apenas com a classificação dos valores dos dados (conforme a classificação de x aumenta, a classificação de y também aumenta?), então a correlação de classificação de Spearman nos daria uma ideia melhor do correlação entre as duas variáveis. .

Neste conjunto de dados específico, à medida que a classificação de x aumenta, a classificação de y sempre aumenta.

A correlação de postos de Spearman captura perfeitamente esse comportamento, dizendo-nos que existe uma relação positiva perfeita ( ρ = 1 ) entre os postos de x e os postos de y.

Por outro lado, a correlação de Pearson diz-nos que existe uma forte relação linear ( r = 0,79 ) entre as duas variáveis.

Isto é verdade, mas não é útil se nos preocuparmos apenas com a relação entre os postos de x e os postos de y.

Cenário 2: Correlação da classificação de Spearman com valores discrepantes extremos

Considere o seguinte conjunto de dados (e o gráfico de dispersão correspondente) que mostra a relação entre duas variáveis:

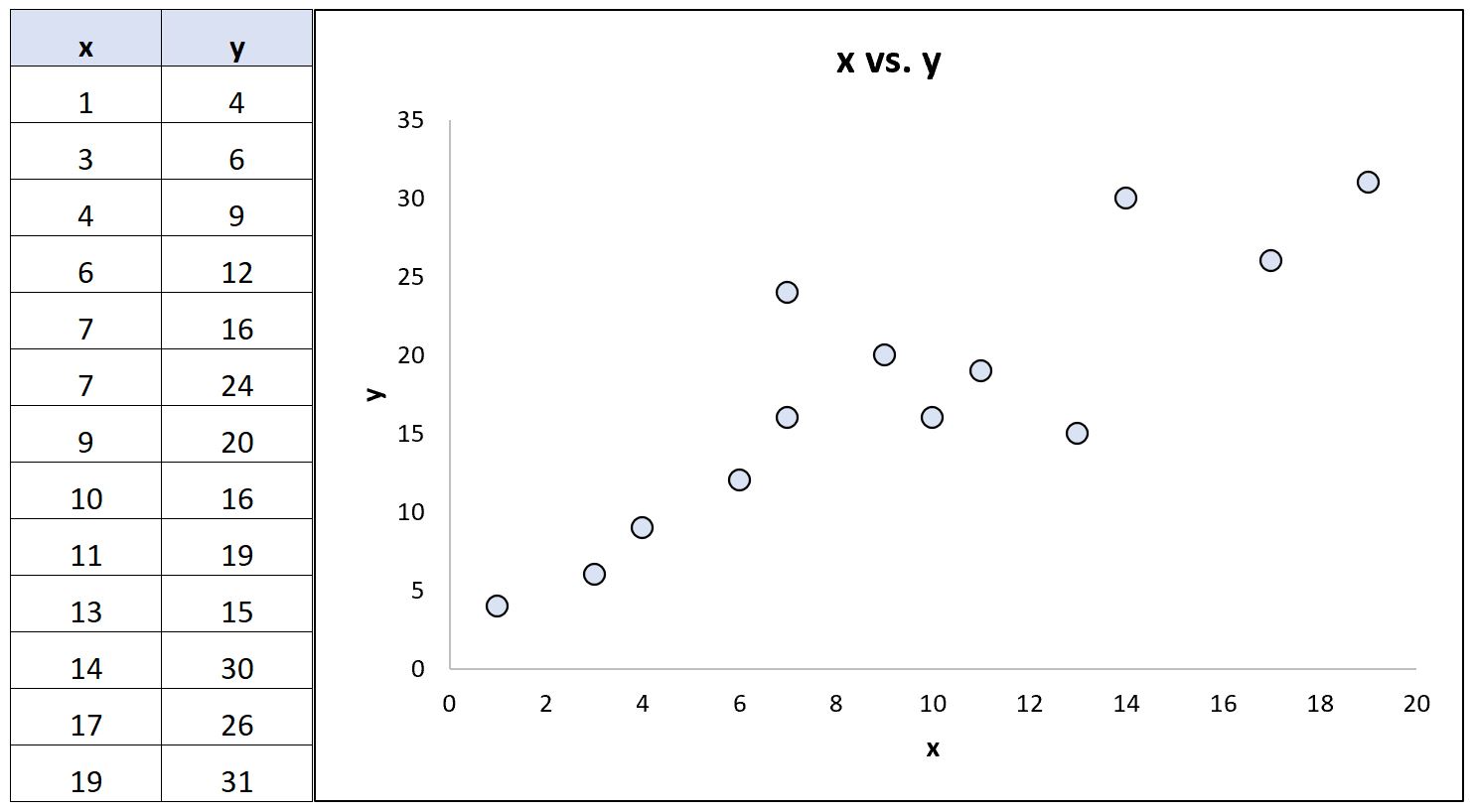
Usando software estatístico, podemos calcular os seguintes coeficientes de correlação para essas duas variáveis:

• Correlação de Pearson: 0,86
• Correlação de classificação de Spearman: 0,85

Os coeficientes de correlação são quase idênticos porque a relação subjacente entre as variáveis é aproximadamente linear e não existem valores discrepantes extremos.

Agora, suponha que alteremos o último valor de y no conjunto de dados para que ele se torne um valor discrepante extremo:

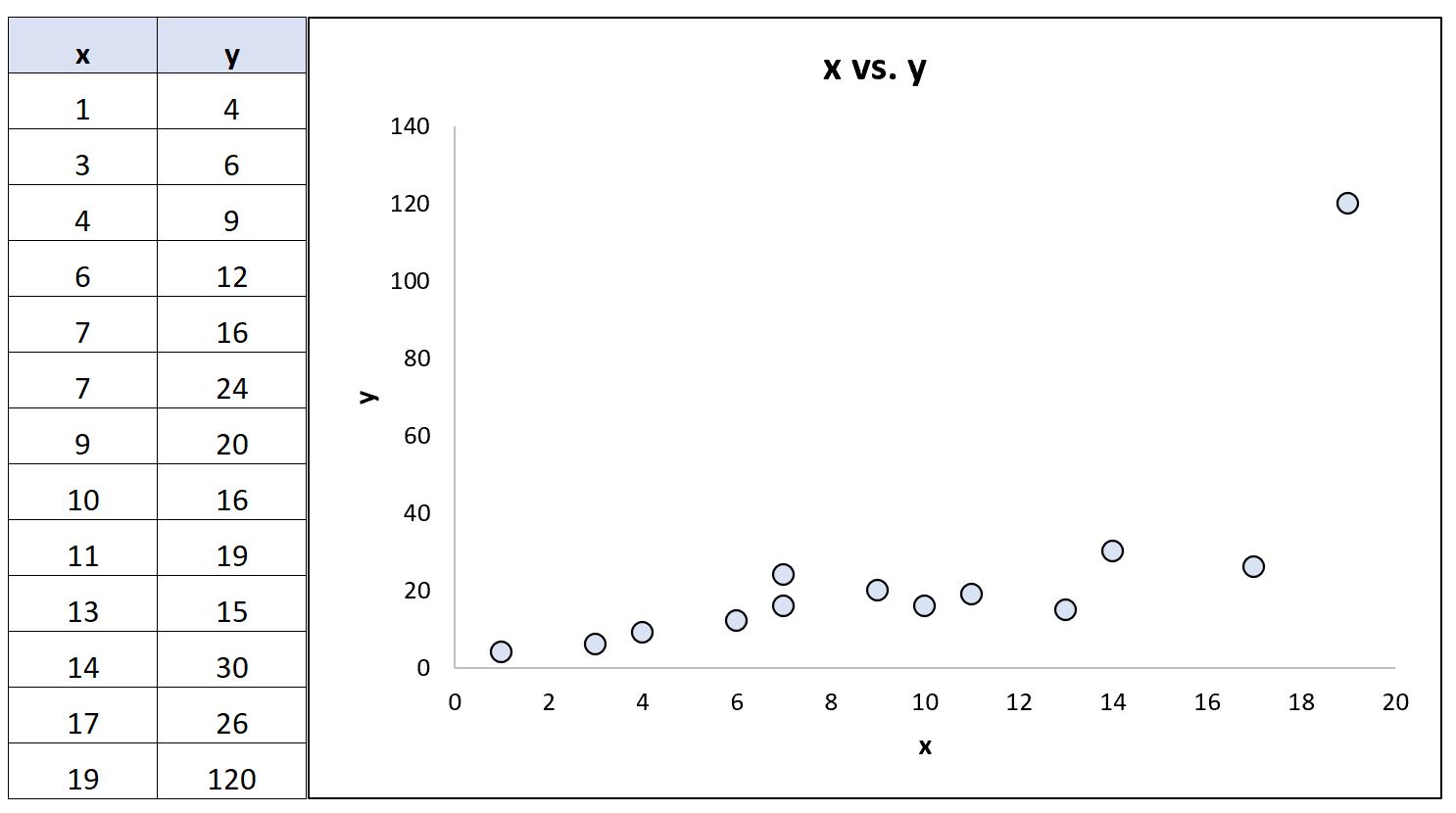
Usando software estatístico, podemos recalcular os coeficientes de correlação:

• Correlação de Pearson: 0,69
• Correlação de classificação de Spearman: 0,85

O coeficiente de correlação de Pearson mudou significativamente, enquanto o coeficiente de correlação de Spearman permaneceu o mesmo.

Usando jargão estatístico, diríamos que a relação entre x e y é monotônica (à medida que x aumenta, y geralmente aumenta), mas não linear, uma vez que o valor discrepante influencia muito os dados.

Neste cenário, a correlação de postos de Spearman quantifica bem esta relação monotónica, enquanto a correlação de Pearson faz um mau trabalho porque tenta calcular a relação linear entre as duas variáveis.

Relacionado: Como relatar a correlação de classificação de Spearman no formato APA

Recursos adicionais

Os tutoriais a seguir explicam como calcular a correlação de classificação de Spearman usando software diferente:

Como calcular a correlação de classificação de Spearman no Excel
Como calcular a correlação de classificação de Spearman no Planilhas Google
Como calcular a correlação de classificação de Spearman em R
Como calcular a correlação de classificação de Spearman em Python