Quando você deve usar correlação? (explicação e exemplos)

A correlação é usada para medir a associação linear entre duas variáveis.

Um coeficiente de correlação sempre assume um valor entre -1 e 1 onde:

• -1 indica uma correlação linear perfeitamente negativa entre duas variáveis
• 0 indica nenhuma correlação linear entre duas variáveis
• 1 indica uma correlação linear perfeitamente positiva entre duas variáveis

Uma pergunta que os alunos costumam fazer é: Quando devo usar a correlação?

A resposta curta: use a correlação quando quiser quantificar a relação linear entre duas variáveis e nenhuma das variáveis representa uma resposta ou variável de “resultado” .

Os exemplos a seguir ilustram quando você deve ou não usar a correlação na prática.

Exemplo 1: Quando usar correlação

Suponha que um professor queira compreender a relação linear entre as notas dos testes de matemática e as notas dos testes de ciências dos alunos de sua turma.

Por exemplo, os alunos que têm um bom desempenho no exame de matemática também se saem bem no exame de ciências? Ou será que os alunos com notas altas em matemática tendem a ter notas baixas em ciências?

Nesse cenário, ele poderia calcular a correlação entre as notas dos exames de matemática e as notas dos exames de ciências porque deseja apenas entender a relação linear entre as duas variáveis e nenhuma das variáveis pode ser considerada uma variável de resposta.

Suponha que ele calcule o coeficiente de correlação de Pearson e descubra que é r = 0,78. Esta é uma forte correlação positiva, o que significa que os alunos com bom desempenho em matemática também tendem a ter bom desempenho em ciências.

Exemplo 2: Quando não usar correlação

Digamos que o departamento de marketing de uma empresa queira quantificar o impacto dos gastos com publicidade na receita total.

Por exemplo, para cada dólar adicional gasto em publicidade, quanta receita adicional a empresa pode esperar obter?

Nesse cenário, o departamento deve utilizar um modelo de regressão linear para quantificar a relação entre os gastos com publicidade e a receita total, pois a variável “receita” é a variável resposta.

Suponha que o departamento aplique um modelo de regressão linear simples e descubra que a seguinte equação descreve melhor a relação entre gastos com publicidade e receita total:

Receita total = 145,4 + 0,34*(despesas com publicidade)

Interpretaríamos isso como significando que cada dólar adicional gasto em publicidade resulta em um aumento médio de US$ 0,34 na receita total.

Precauções para usar correlação

É importante notar que a correlação só pode ser usada para quantificar a relação linear entre duas variáveis.

Contudo, em certas circunstâncias, um coeficiente de correlação não será capaz de captar eficazmente uma relação entre duas variáveis que partilham uma relação não linear.

Por exemplo, suponha que criemos o seguinte gráfico de dispersão para visualizar a relação entre duas variáveis:

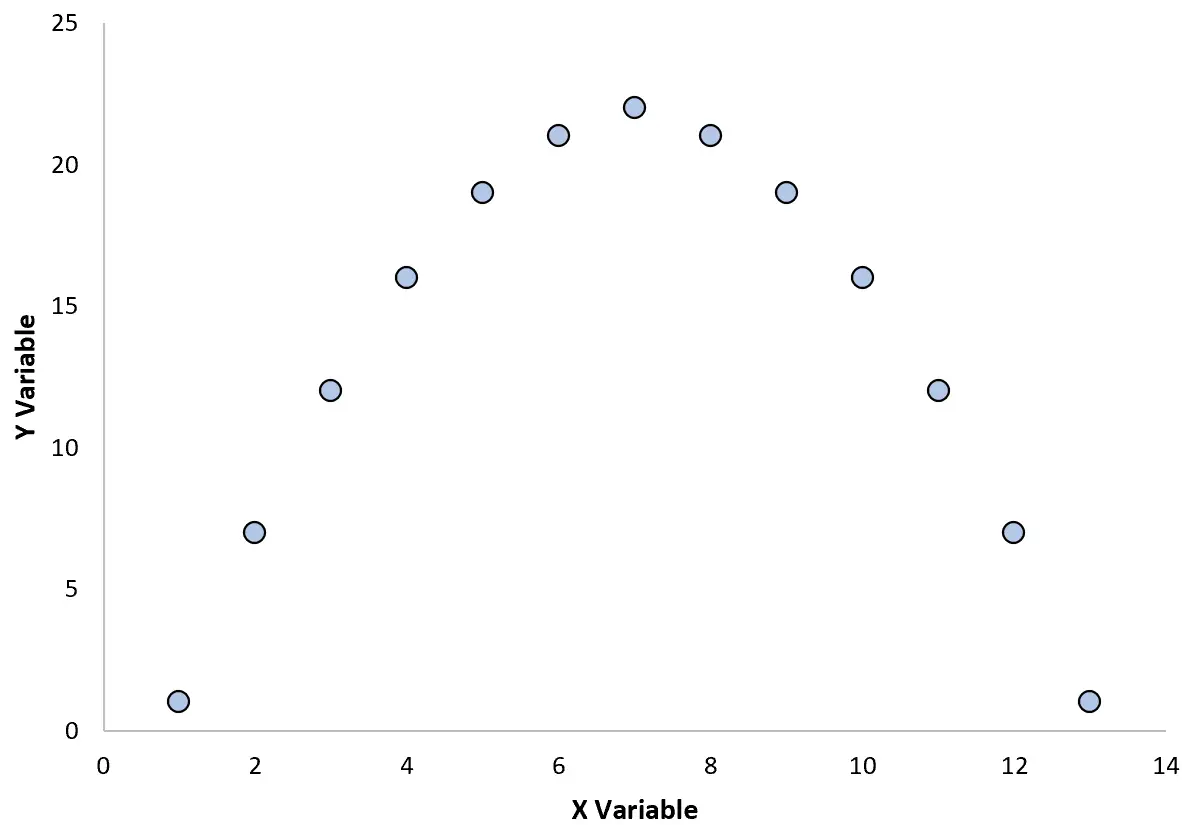
Se calcularmos o coeficiente de correlação entre estas duas variáveis, verifica-se que é r = 0. Isto significa que não existe uma relação linear entre as duas variáveis.

No entanto, a partir do gráfico podemos ver que as duas variáveis têm de facto uma relação – é simplesmente uma relação quadrática em vez de uma relação linear.

Portanto, ao calcular a correlação entre duas variáveis, lembre-se que também pode ser útil criar um gráfico de dispersão para visualizar a relação entre as variáveis.

Mesmo que duas variáveis não tenham uma relação linear, é possível que tenham uma relação não linear que seria revelada num gráfico de dispersão.

Recursos adicionais

Os tutoriais a seguir explicam com mais detalhes como a correlação é usada em diferentes circunstâncias:

6 exemplos reais de correlação
O que é considerado uma correlação “forte”?
Correlação vs. associação: qual é a diferença?
Correlação vs regressão: qual a diferença?