Quando você deve usar um box plot? (3 cenários)
Um box plot é um tipo de gráfico que exibe o resumo de cinco dígitos de um conjunto de dados, que inclui:
- O valor mínimo
- O primeiro quartil (o 25º percentil)
- O valor mediano
- O terceiro quartil (o 75º percentil)
- O valor máximo
Usamos três etapas simples para criar um box plot para qualquer conjunto de dados:
- 1. Desenhe uma caixa do primeiro ao terceiro quartil
- 2. Desenhe uma linha vertical na mediana
- 3. Desenhe “bigodes” dos quartis para o valor mínimo e máximo

Normalmente criamos boxplots em um dos três cenários:
Cenário 1: Visualize a distribuição de valores em um conjunto de dados.
Um box plot nos permite visualizar rapidamente a distribuição de valores em um conjunto de dados e ver onde estão localizados os cinco valores numéricos de resumo.
Cenário 2: Comparar duas ou mais distribuições.
Os boxplots lado a lado nos permitem visualizar as diferenças entre duas ou mais distribuições e comparar os valores medianos e a distribuição dos valores entre as distribuições.
Cenário 3: Para identificar outliers.
Em box plots, os valores discrepantes são geralmente representados por pequenos círculos que se estendem além de cada bigode. Uma observação é definida como outlier se atender a um dos seguintes critérios:
- Uma observação é menor que Q1 – 1,5*(intervalo interquartil)
- Uma observação é maior que Q3 + 1,5*(intervalo interquartil)
Ao criar um box plot, podemos ver rapidamente se uma distribuição tem ou não valores discrepantes.
Os exemplos a seguir mostram como usaríamos um box plot em cada cenário.
Cenário 1: Visualize a distribuição de valores em um conjunto de dados
Suponha que um treinador de basquete queira visualizar a distribuição de pontos marcados pelos jogadores de seu time e, portanto, crie o seguinte box plot:
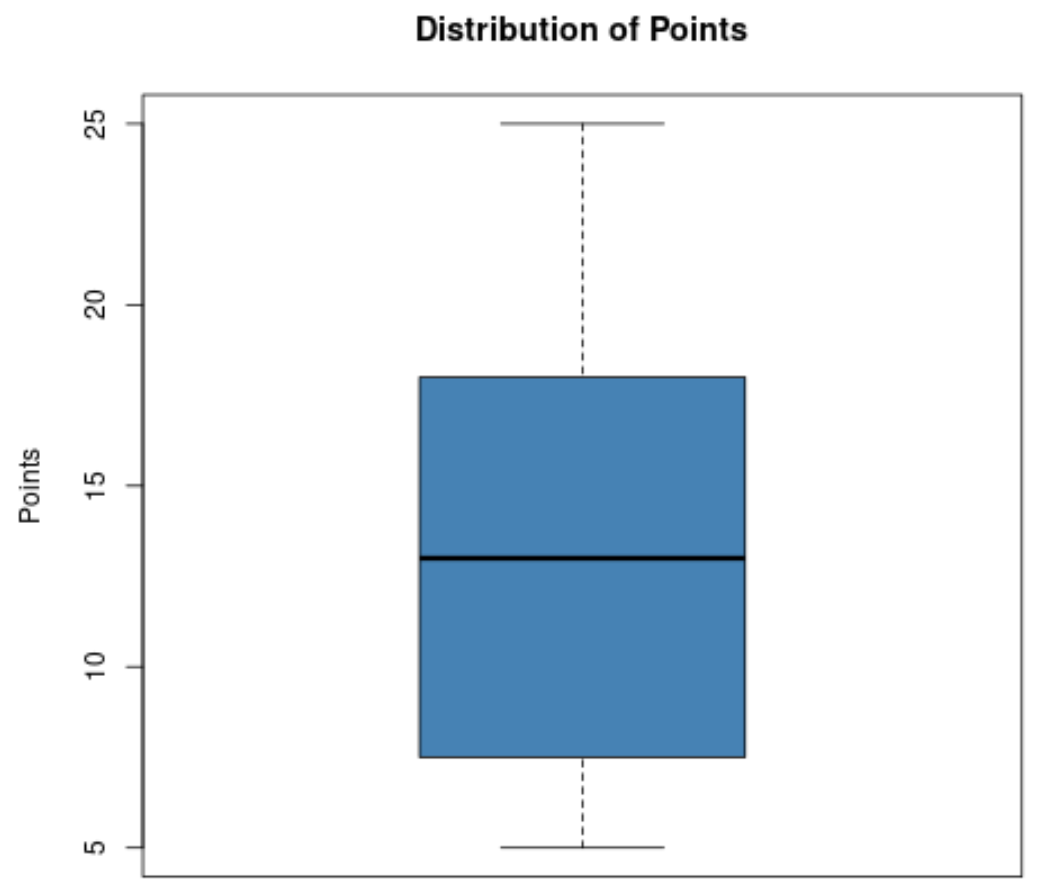
Com base neste box plot, ele pode ver rapidamente os seguintes valores:
- Mínimo: 5
- T1 (primeiro quartil): aproximadamente 8
- Mediana: cerca de 13
- T3 (terceiro quartil): aproximadamente 18
- Máximo: 25
Isto permite ao treinador ver rapidamente que os pontos marcados pelos jogadores variam entre 5 e 25, que a mediana de pontos marcados é de aproximadamente 13 e que 50% dos seus jogadores marcam entre aproximadamente 8 e 18 pontos por jogo.
Cenário 2: Compare duas ou mais distribuições
Suponha que um analista esportivo queira comparar a distribuição de pontos marcados por jogadores de basquete em três times diferentes e crie os seguintes box plots:
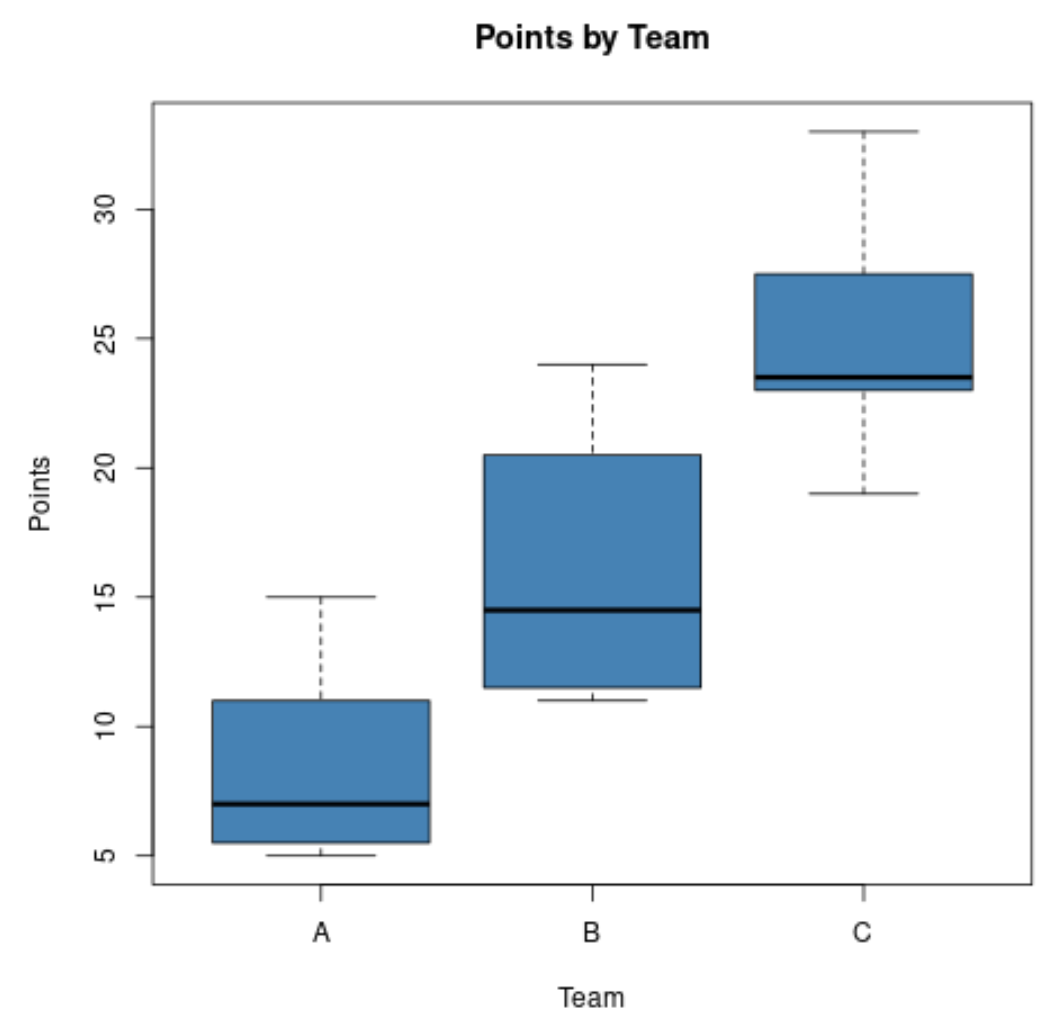
Usando esses gráficos, ele pode ver rapidamente que a Equipe C tem os pontos médios mais altos e a Equipe A tem os pontos médios mais baixos.
Ele também pode ver rapidamente que o Time B tem a maior distribuição de pontos marcados, já que o box plot do Time B tem o box plot mais longo.
Cenário 3: Identificar valores discrepantes
Suponha que um treinador de basquete queira saber se um de seus jogadores é atípico em termos de pontos marcados. Ele decide criar o seguinte box plot para visualizar a distribuição dos pontos marcados por seus jogadores:
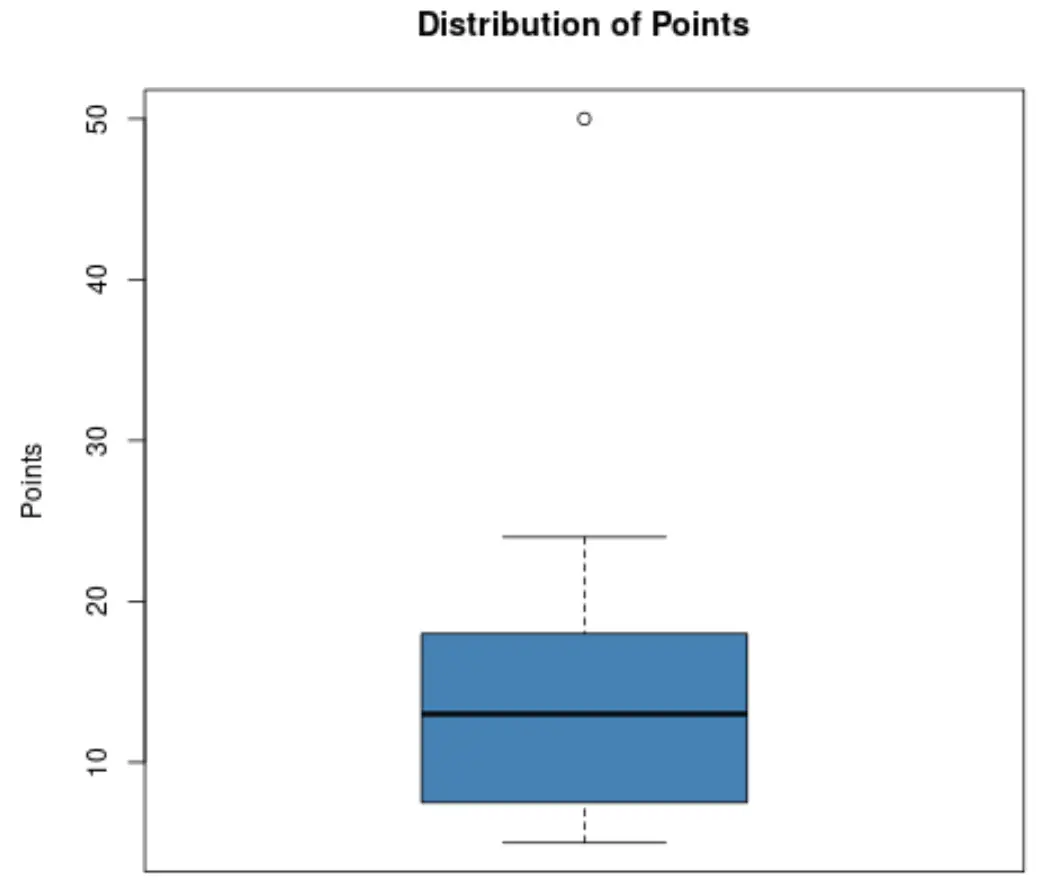
Usando este gráfico, o treinador pode ver que o pequeno ponto no topo do gráfico indica um valor atípico.
Especificamente, um dos jogadores marcou cerca de 50 pontos, o que é considerado um valor atípico em comparação com todos os outros pontos marcados.
Recursos adicionais
Os tutoriais a seguir oferecem explicações detalhadas sobre como usar boxplots na prática:
Como encontrar o intervalo interquartil (IQR) de um box plot
Como identificar assimetria em box plots
Como comparar gráficos de caixa
Os tutoriais a seguir explicam como criar box plots em diferentes softwares estatísticos:
Como criar um box plot no Planilhas Google
Como criar gráficos de caixa no SPSS
Como criar gráficos de caixa lado a lado no Excel
Como criar gráficos de caixa lado a lado em R