Quasevariância

Este artigo explica o que é quase variância nas estatísticas. Assim, você descobrirá como calcular a quase-variância, um exercício resolvido e quais as diferenças entre a quase-variância e a variância. Além disso, você pode calcular a quase-variância de qualquer conjunto de dados com uma calculadora online.

O que é quase variância?

Nas estatísticas, a quasevariância é uma medida de dispersão que indica a variabilidade de uma amostra. Mais precisamente, a quasevariância é igual à soma dos quadrados dos desvios dividida pelo número total de observações menos um.

O símbolo para quase variância é

qualquer

. às vezes Embora o símbolo também seja usado

para representar a quasevariância.

A quase-variância é usada para determinar a dispersão de uma amostra, evitando viés, razão pela qual é frequentemente chamada de variância imparcial. A quasevariância é, portanto, um bom estimador da variância populacional. Na verdade, ao calcular a variância da amostra, a fórmula de quase variância é frequentemente usada em vez da fórmula de variância. A seguir entraremos em detalhes sobre a diferença entre essas duas medidas estatísticas.

Fórmula de quasevariância

Para calcular a quasevariância, é necessário encontrar a soma dos quadrados das diferenças entre os valores e a média do conjunto de dados e posteriormente dividi-la pelo número total de dados menos um.

Portanto, a fórmula para calcular a quasevariância é a seguinte:

Ouro:

• 

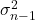
  é a quasevariância.

• 

  é o valor dos dados

  

  .

• 

  é o número total de dados.

• 

  é a média do conjunto de dados.

👉 Você pode usar a calculadora abaixo para calcular a quase variância de qualquer conjunto de dados.

Você pode estar se perguntando por que é dividido por n-1 e não por n? Bom, trata-se de eliminar o viés, assim obtemos um estimador imparcial. É precisamente por isso que a quasevariância é um bom estimador da variância populacional.

Exemplo de cálculo de quase variância

Agora que conhecemos a definição de quase-variância, resolveremos um exemplo simples para que você possa ver como a quase-variância de uma série de dados é calculada.

• De uma empresa multinacional conhecemos o resultado económico que teve nos últimos cinco anos, na sua maioria obteve lucros mas num ano apresentou perdas consideráveis: 11,5, 2, -9, 7 milhões de euros. Calcule a quasevariância deste conjunto de dados.

A primeira coisa que precisamos fazer para obter a quase-variância de um conjunto de dados é calcular sua média aritmética:

E uma vez conhecido o valor médio dos dados, aplicamos a fórmula de quase variância:

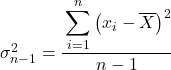
Portanto, substituímos os dados fornecidos pelas instruções do exercício na fórmula:

Por fim, basta resolver as operações para calcular a quasevariância:

Observe que as unidades da quase-variância são as mesmas unidades dos dados estatísticos, mas ao quadrado, portanto, a quase-variância deste conjunto de dados é 57,2 milhões ² .

Calculadora de quase variância

Insira um conjunto de dados estatísticos na calculadora a seguir para calcular sua quase-variância. Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.

Variância e quasevariância

Por fim, veremos a diferença entre quase-variância e variância, pois apesar da semelhança no nome, também são calculadas de forma muito semelhante.

A diferença entre a quase-variância e a variância é o denominador da fórmula. Para calcular a quase-variância, você deve dividir por n-1, porém, a variância é calculada dividindo por n.

Assim, a quase-variância e a variância estão matematicamente relacionadas, uma vez que a quase-variância é equivalente à variância multiplicada por n (o número total de pontos de dados) e dividida por n-1.

Portanto, para o mesmo conjunto de dados, o valor da quase-variância será sempre maior que o valor da variância.