R vs r-quadrado: qual a diferença?

Dois termos que os estudantes muitas vezes confundem em estatística são R e R-quadrado , muitas vezes escritos ^R2 .

No contexto de uma regressão linear simples :

• A: A correlação entre a variável preditora, x, e a variável de resposta, y.
• R ² : Proporção da variância da variável resposta que pode ser explicada pela variável preditora no modelo de regressão.

E no contexto de uma regressão linear múltipla :

• A: A correlação entre os valores observados da variável resposta e os valores previstos da variável resposta feitos pelo modelo.
• R ² : Proporção da variância da variável resposta que pode ser explicada pelas variáveis preditoras do modelo de regressão.

Observe que o valor de R ² está entre 0 e 1. Quanto mais próximo o valor estiver de 1, mais forte será a relação entre a(s) variável(ões) preditora(s) e a variável resposta.

Os exemplos a seguir mostram como interpretar os valores de R e R ao quadrado em modelos de regressão linear simples e de regressão linear múltipla.

Exemplo 1: Regressão linear simples

Suponha que temos o seguinte conjunto de dados que mostra as horas estudadas e as notas dos exames obtidas por 12 alunos em um determinado curso de matemática:

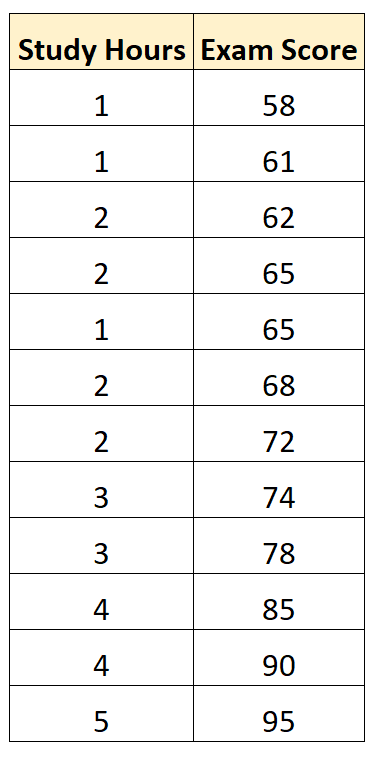
Usando software estatístico (como Excel, R, Python, SPSS, etc.), podemos ajustar um modelo de regressão linear simples usando “horas de estudo” como variável preditora e “nota do exame” como variável de resposta .

Podemos encontrar a seguinte saída para este modelo:

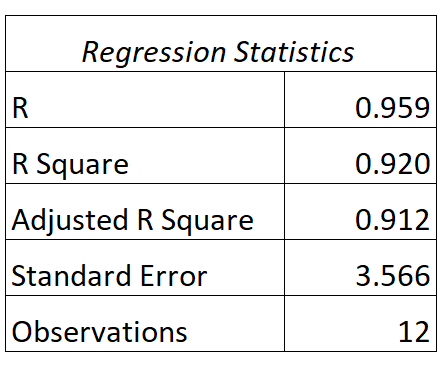
Veja como interpretar os valores de R e R ao quadrado deste modelo:

• R: A correlação entre horas estudadas e nota do exame é de 0,959 .
• R ² : O R ao quadrado para este modelo de regressão é 0,920 . Isso nos diz que 92,0% da variação nas notas dos exames pode ser explicada pela quantidade de horas estudadas.

Observe também que o valor de R ² é simplesmente igual ao valor de R, ao quadrado:

^R2 = R * R = 0,959 * 0,959 = 0,920

Exemplo 2: Regressão linear múltipla

Suponha que temos o seguinte conjunto de dados que mostra as horas estudadas, a nota atual do aluno e a nota do exame obtida por 12 alunos em um determinado curso de matemática:

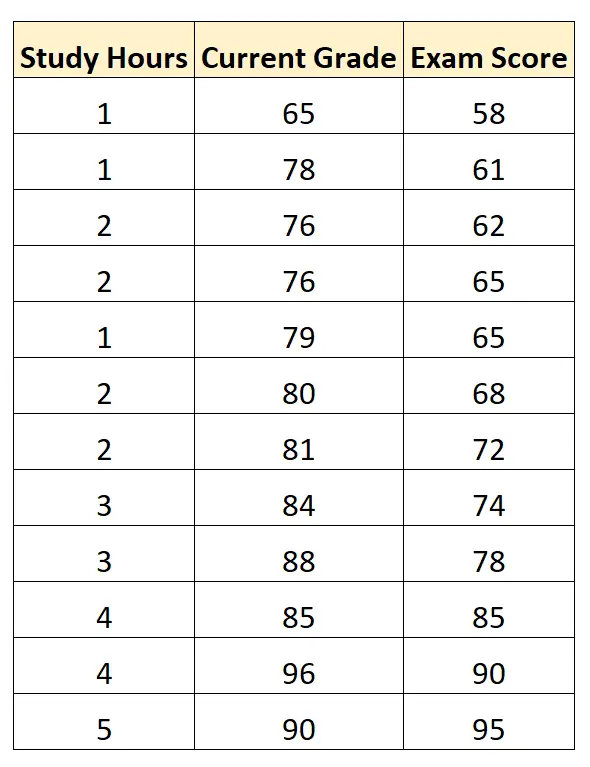
Usando software estatístico, podemos ajustar um modelo de regressão linear múltipla usando “horas de estudo” e “nota atual” como variáveis preditoras e “nota no exame” como variável resposta.

Podemos encontrar a seguinte saída para este modelo:

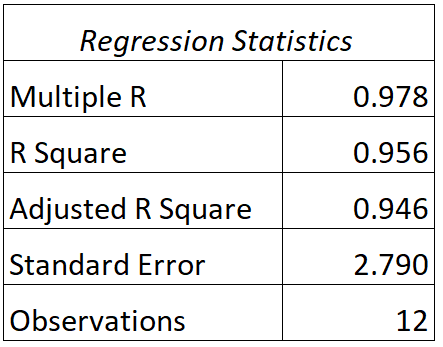
Veja como interpretar os valores de R e R ao quadrado deste modelo:

• R: A correlação entre as pontuações reais dos testes e as pontuações previstas dos testes do modelo é 0,978 .
• R ² : O R ao quadrado para este modelo de regressão é 0,956 . Isso nos diz que 95,6% da variação nas notas dos exames pode ser explicada pela quantidade de horas estudadas e pela nota atual do aluno na turma.

Observe também que o valor de R ² é simplesmente igual ao valor de R, ao quadrado:

^R2 = R * R = 0,978 * 0,978 = 0,956

Recursos adicionais

O que é um bom valor de R ao quadrado?
Um guia suave para a soma dos quadrados: SST, SSR, SSE