Razão de chances versus risco relativo: qual a diferença?

Dois termos que os estudantes muitas vezes confundem nas estatísticas são razão de probabilidade e risco relativo .

Freqüentemente usamos essas duas métricas ao analisar uma tabela 2 por 2, que assume o seguinte formato:

A razão de chances nos diz a razão entre a probabilidade de um evento ocorrer em um grupo de tratamento e a probabilidade de um evento ocorrer em um grupo de controle. É calculado da seguinte forma:

Proporção de probabilidades = (A*D) / (B*C)

O risco relativo nos diz a razão entre a probabilidade de um evento ocorrer em um grupo de tratamento e a probabilidade de um evento ocorrer em um grupo de controle. É calculado da seguinte forma:

Risco relativo = [A/(A+B)] / [C/(C+D)]

Resumindo, aqui está a diferença:

• Uma razão de probabilidades é uma proporção de duas probabilidades .
• O risco relativo é uma razão entre duas probabilidades .

O exemplo a seguir mostra como calcular e interpretar uma razão de chances e um risco relativo em uma situação do mundo real.

Exemplo: cálculo da razão de chances e risco relativo

Suponha que 100 jogadores de basquete usem um novo programa de treinamento e 100 jogadores usem um programa de treinamento antigo. No final do programa, testamos cada jogador para ver se ele passa em determinado teste de habilidade.

A tabela a seguir mostra o número de jogadores que passaram e falharam, com base no programa que utilizaram:

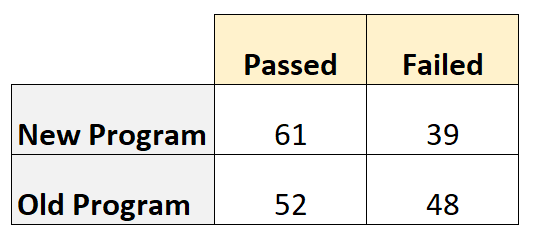
A razão de chances é calculada da seguinte forma:

• Proporção de probabilidades = (A*D) / (B*C)
• Proporção de probabilidades = (61*48) / (39*52)
• Razão de probabilidade = 1,44

Interpretaríamos isso como significando que as chances de um jogador passar no teste usando o novo programa são 1,44 vezes as chances de um jogador passar no teste usando o programa antigo.

Ou seja, as chances de um jogador passar no teste aumentam com a utilização do novo programa.

O risco relativo é calculado como

• Risco relativo = [A/(A+B)] / [C/(C+D)]
• Risco relativo = [61/(61+39)] / [52/(52+48)]
• Risco relativo = 1,17

Interpretaríamos isso como significando que a razão entre a probabilidade de um jogador passar no teste usando o novo programa e o programa antigo é 1,17 .

Como este valor é maior que 1, isso nos diz que a probabilidade de sucesso é maior no novo programa do que no programa antigo.

Também podemos ver isso calculando diretamente a probabilidade de um jogador passar em cada programa:

Probabilidade de sucesso no novo programa = 61/100 = 61%

Probabilidade de sucesso no programa antigo = 52/100 = 52%

Tomando a razão dessas probabilidades, podemos calcular o risco relativo como 61%/52% = 1,17 .

Observe que a razão de chances e o risco relativo são ambos maiores que 1, o que nos diz que as chances de vivenciar um evento (por exemplo, passar no teste de habilidades) são maiores no grupo de tratamento do que no grupo de controle.

A razão de probabilidade e o risco relativo fornecem-nos informações semelhantes, mas interpretamos cada valor de forma ligeiramente diferente.

Especialmente:

• A razão de probabilidades diz-nos que as probabilidades de passar no teste de competências são maiores no novo programa.
• O risco relativo diz-nos que a probabilidade de passar no teste de competências é maior no novo programa.

Usando qualquer uma das métricas, podemos ver facilmente que o novo programa é melhor que o antigo.

Recursos adicionais

Os tutoriais a seguir oferecem informações adicionais sobre odds ratio e risco relativo:

Como interpretar razões de probabilidade
Como interpretar o risco relativo
Como calcular a razão de chances e o risco relativo no Excel