Regra de adição (ou regra de adição)

By Dr. benjamim anderson Agosto 1, 2023 Probabilidade 0 Comments

Este artigo explica o que é a regra de adição, também conhecida como regra de adição, e para que ela é usada em probabilidade e estatística. Além disso, você poderá ver qual é a fórmula da regra de adição e resolver exercícios que mostram como utilizá-la.

Qual é a regra de adição (ou regra de adição)?

A regra da adição (ou regra da adição ) afirma que a soma das probabilidades de dois eventos é igual à soma da probabilidade de cada evento ocorrer separadamente menos a probabilidade de ambos os eventos ocorrerem ao mesmo tempo.

Portanto, a fórmula para a regra de adição é P(A⋃B)=P(A)+P(B)−P(A⋂B).

Assim, para somar duas probabilidades, não podemos simplesmente somar cada probabilidade, pois devemos também subtrair o termo que representa a probabilidade conjunta dos dois eventos. Porém, em alguns casos, somente somando a probabilidade de cada evento podemos obter o resultado correto da soma das probabilidades. A seguir veremos quais são esses casos.

Resumindo, a regra da adição é utilizada para calcular a probabilidade de ocorrência de um evento ou outro, ou seja, a probabilidade de ocorrer pelo menos um de dois eventos possíveis.

Fórmula de regra de adição

A regra de adição diz que para calcular a probabilidade de ocorrência do evento A ou B, devemos adicionar a probabilidade de ocorrência do evento A mais a probabilidade de ocorrência do evento B e subtrair a probabilidade de ambos os eventos ocorrerem ao mesmo tempo. .

A fórmula para a regra de adição (ou regra de adição) é, portanto, a seguinte:

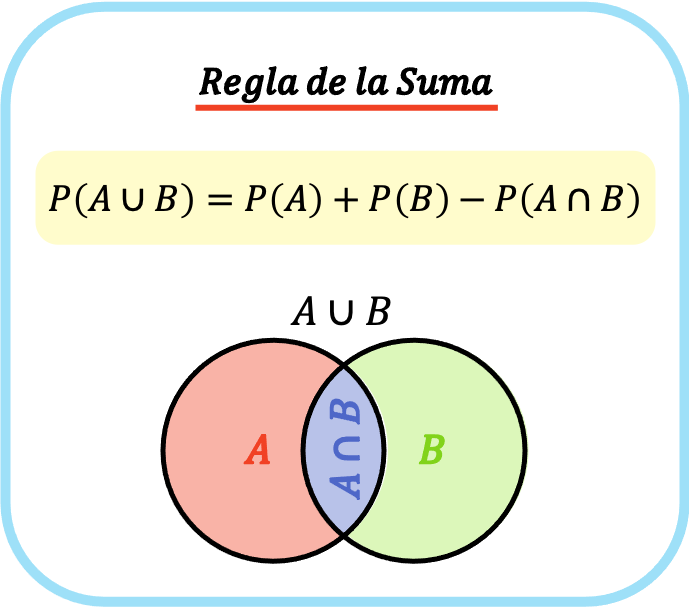
fórmula de regra de adição, fórmula de regra de adição

Ouro:

$P(A\cup B)$

é a probabilidade do evento A ou do evento B.
$P(A)$

é a probabilidade de que o evento A ocorra.
$P(B)$

é a probabilidade de que o evento B ocorra.
$P(A\cap B)$

é a probabilidade conjunta de que o evento A e o evento B ocorram.

Portanto, para usar a regra da soma, você precisa saber como calcular a probabilidade conjunta de dois eventos. Você pode ver como isso é feito no seguinte link:

➤ Veja: Como calcular a probabilidade conjunta

Exemplo de regra de soma para eventos exclusivos

Para finalizar a compreensão do conceito, vejamos um exemplo de como aplicar a regra de adição.

Colocamos 10 bolas azuis, 6 bolas laranja e 4 bolas verdes numa caixa. Qual é a probabilidade de tirar uma bola azul ou laranja?

O exercício pede-nos para determinar a probabilidade de um evento ou outro ocorrer. Portanto, para resolver o problema, precisamos usar a fórmula da regra de adição:

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Então, primeiro calculamos a probabilidade de cada evento ocorrer separadamente usando a regra de Laplace :

$P(\text{bola azul})=\cfrac{10}{10+6+4}=0,5$

$P(\text{bola naranja})=\cfrac{6}{10+6+4}=0,3$

Porém, neste caso, os dois eventos não podem ocorrer ao mesmo tempo, pois são dois eventos mutuamente exclusivos . Portanto, se desenharmos uma bola azul não poderemos mais desenhar uma bola laranja e vice-versa.

Portanto, a probabilidade conjunta de ambos os eventos é zero e, portanto, a fórmula da regra da soma é simplificada:

$P(A\cup B)=P(A)+P(B)-\cancelto{0}{P(A\cap B)}$

Portanto, o cálculo da probabilidade de pegar uma bola azul ou laranja é o seguinte:

$\begin{aligned}P(\text{bola azul}\cup \text{bola naranja})&=P(\text{bola azul})+P(\text{bola azul})\\[2ex]&=0,5+0,3\\[2ex]&=0,8\end{aligned}$

Resumindo, a probabilidade de tirar uma bola azul ou laranja da caixa é de 80%.

Exemplo de regra de acréscimo para eventos não exclusivos

Tendo visto um exemplo concreto da regra da adição quando os eventos são exclusivos, veremos agora como esta lei é utilizada quando os eventos são não exclusivos.

Se lançarmos uma moeda duas vezes, qual é a probabilidade de obtermos cara em pelo menos um lançamento?

Nesse caso, os eventos não são mutuamente exclusivos, pois podemos obter “cara” no primeiro lance e “coroa” no segundo lance. A fórmula para a regra de adição, portanto, não é simplificada e é a seguinte:

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Portanto, primeiro precisamos calcular a probabilidade de obter “cara” no lançamento de uma moeda, aplicando a regra de Laplace:

$P(\text{cara})=\cfrac{1}{2}=0,5$

Além disso, os dois eventos são independentes, portanto podemos calcular a probabilidade conjunta dos dois eventos usando a regra do produto :

$P(\text{cara}\cap \text{cara})=\cfrac{1}{2}\cdot \cfrac{1}{2}=0,5\cdot 0,5=0,25$

Por fim, para encontrar a probabilidade de cair cara em pelo menos um dos dois lançamentos, basta substituir os valores na fórmula da regra de adição e fazer o cálculo:

$\begin{aligned}P(\text{cara}\cup \text{cara})&=P(\text{cara})+P(\text{cara})-P(\text{cara}\cap \text{cara})\\[2ex]&=0,5+0,5-0,25\\[2ex]&=0,75\end{aligned}$

Concluindo, a probabilidade de que, ao lançar uma moeda duas vezes, dê cara pelo menos uma vez é de 75%.

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais