Como realizar regressão cúbica em python

A regressão cúbica é um tipo de regressão que podemos usar para quantificar a relação entre uma variável preditora e uma variável de resposta quando a relação entre as variáveis é não linear.

Este tutorial explica como realizar regressão cúbica em Python.

Exemplo: regressão cúbica em Python

Suponha que temos o seguinte DataFrame do pandas que contém duas variáveis (x e y):

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' x ': [6, 9, 12, 16, 22, 28, 33, 40, 47, 51, 55, 60],
                   ' y ': [14, 28, 50, 64, 67, 57, 55, 57, 68, 74, 88, 110]})

#view DataFrame
print (df)

     xy
0 6 14
1 9 28
2 12 50
3 16 64
4 22 67
5 28 57
6 33 55
7 40 57
8 47 68
9 51 74
10 55 88
11 60 110

Se fizermos um gráfico de dispersão simples desses dados, podemos ver que a relação entre as duas variáveis é não linear:

 import matplotlib. pyplot as plt

#create scatterplot
plt. scatter (df. x , df. y ) 

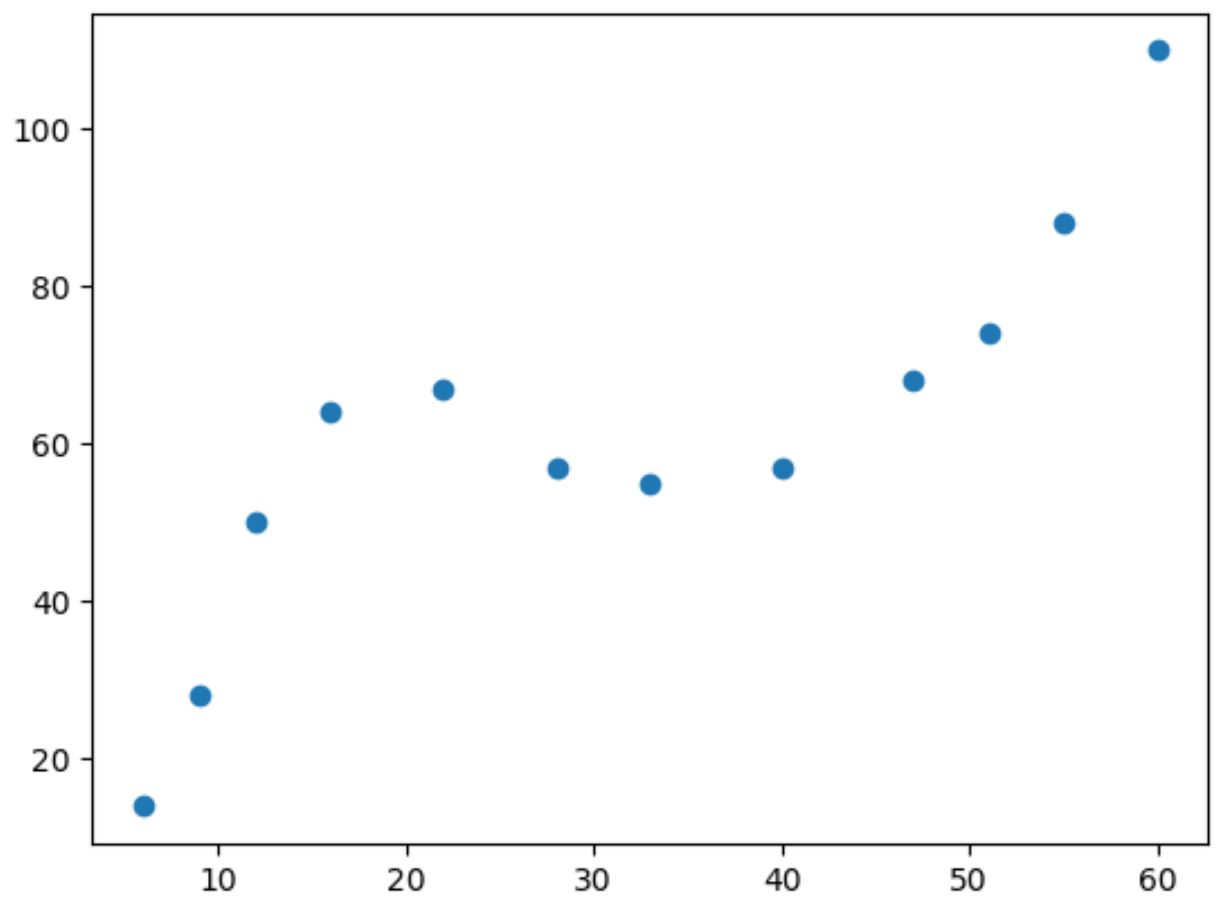
À medida que o valor de x aumenta, y aumenta até certo ponto, depois diminui e depois aumenta novamente.

Este padrão com duas “curvas” no gráfico é uma indicação de uma relação cúbica entre as duas variáveis.

Isto significa que um modelo de regressão cúbico é um bom candidato para quantificar a relação entre as duas variáveis.

Para realizar a regressão cúbica, podemos ajustar um modelo de regressão polinomial com grau 3 usando a função numpy.polyfit() :

 import numpy as np

#fit cubic regression model
model = np. poly1d (np. polyfit (df. x , df. y , 3))

#add fitted cubic regression line to scatterplot
polyline = np. linspace (1, 60, 50)
plt. scatter (df. x , df. y )
plt. plot (polyline, model(polyline))

#add axis labels
plt. xlabel (' x ')
plt. ylabel (' y ')

#displayplot
plt. show () 

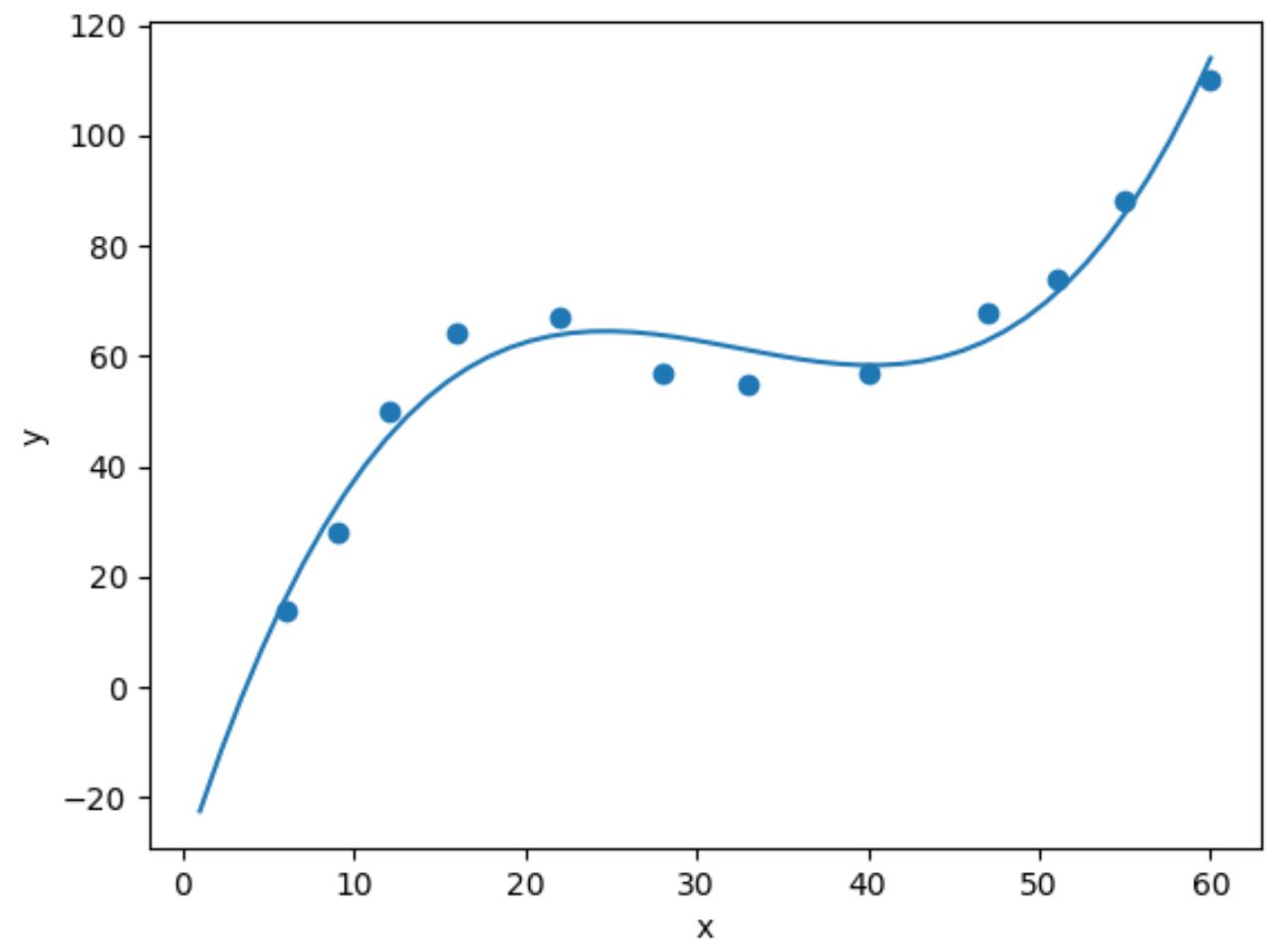
Podemos obter a equação de regressão cúbica ajustada imprimindo os coeficientes do modelo:

 print (model)

          3 2
0.003302x - 0.3214x + 9.832x - 32.01

A equação de regressão cúbica ajustada é:

y = 0,003302(x) ³ – 0,3214(x) ² + 9,832x – 30,01

Podemos usar esta equação para calcular o valor esperado de y com base no valor de x.

Por exemplo, se x for 30, então o valor esperado para y é 64,844:

y = 0,003302(30) ³ – 0,3214(30) ² + 9,832(30) – 30,01 = 64,844

Também podemos escrever uma função curta para obter o R-quadrado do modelo, que é a proporção da variância na variável de resposta que pode ser explicada pelas variáveis preditoras.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar) ** 2)
    sstot = np. sum ((y - ybar) ** 2)
    results[' r_squared '] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(df. x , df. y , 3)

{'r_squared': 0.9632469890057967}

Neste exemplo, o R quadrado do modelo é 0,9632 .

Isso significa que 96,32% da variação da variável resposta pode ser explicada pela variável preditora.

Por ser tão alto, esse valor nos diz que o modelo de regressão cúbica quantifica bem a relação entre as duas variáveis.

Relacionado: O que é um bom valor de R ao quadrado?

Recursos adicionais

Os tutoriais a seguir explicam como realizar outras tarefas comuns em Python:

Como realizar regressão linear simples em Python
Como realizar regressão quadrática em Python
Como realizar regressão polinomial em Python